
interpreted:and the equivalent compiled versions are presented as:
compiled:The difference between the 2 modes is that the interpreted version depends on a set of precompiled functions to accomplish standard programming features such as subroutines, loops, conditionals, and arithmetic using a stack. Therefore the intepreter runs several-fold slower than the compiled version when executing loops and arithmetic. The advantage of the interpreted version is that it runs immediately and can be used like a calculator as in the original version of "hoc" described in Kernighan and Pike (1984) "The Unix Programming Environment".
In the "construction" mode, one can perform simple calculations, program loops, procedures and subroutines to define neural elements. You may organize these procedures to create a neuron or circuits of many neurons. You may also include stimuli and records in loops and procedures. "Construction" mode is familiar to computer programmers because it is similar to a language like "C" in which procedures are used to accomplish tasks.
A simple calculation:
(interpreted only:)
print 54/7; (prints simple calculations)
A print statement within a loop:
for (i=0; i<10; i++)
print i, sqrt(i); (prints square roots)
To define a circuit, add a neural element definition:
(interpreted:)
for (i=1; i<=5; i++) (makes a tapered cable)
conn i to i-1 cable dia 10-i length 10;
(compiled:)
for (i=1; i<=5; i++)
{c = conn(nd(i), nd(i-1), CABLE); c->dia=10-i; c->length=10;}
statement 1; (these statements construct neural circuit)
statement 2;
statement 3;
.
.
.
step .05; (stops circuit construction, runs 50 msec)
Normally you want to run a simulation as fast as possible. In Neuron-C it is faster to set stimuli and plots before exiting from "construction mode" into "run mode". Then the stimuli and plots run automatically at the correct times in the way you have defined:
Normal order of simulation script:
timinc = <expr> /* set integration time step (default 1e-4 s) */
endexp = <expr> /* set end of simulation */
set_stimuli();
set_plots();
run; /* run simulation until end, set by "endexp". */
Sometimes, a simulation is organized as a set of trials, where a stimulus is repeated and plots are overlaid. Often in this case you want to plot the data always starting at the same time. An easy way to do this is to set "time" back to 0 at the beginning of each trial.
Each time "run mode" stops at the end of a "step" statement, the variable "time" is set to a new value. You can use this variable like any other variable for arithmetic expressions. It is possible to set it backwards or forwards to a different value, however if you do this and start "run mode" again you will change the next starting time of the simulation.
timinc = <expr> /* set integration time step (default 1e-4 s) */
set_plots();
for (i=0; i<=ntrials; i++) { /* repeating trials */
time = 0;
set_stimuli();
step trial_dur; /* run simulation extended time interval */
};
Note that incrementing the "time" variable does not move the simulation forward, since this happens only during a "step" or "run" statement. Although you can change "time" to a new value in construction mode, and you can use this value in expressions, e.g. to define the start time for stimuli, this new value only affects stimuli when run mode starts inside the step statement. The value of the "time" variable is given to the simulator for its internal value of "simulation time" only when run mode starts inside a "step" or "run" statement.
If you have created stimuli, you may lose part of the stimuli and generate unpredictable results if you set time backwards before you run the simulation long enough to play all the stimuli:
TO = 1;
FRO = -1;
predur = .01; /* equilibration time before model runs */
time = 0 - predur; /* sets time negative to allow equilib. time */
setxmin = 0; /* sets x-axis beginning at time=0 */
sdur = 0.1;
durtotal = sdur + predur;
stim sine contrast 0.4 inten .01 tfreq 10 drift TO start time dur durtotal;
step sdur; (this is incorrect)
time = 0;
stim sine contrast 0.4 inten .01 tfreq 10 drift FRO start time dur sdur;
step sdur;
This above example doesn't run the stimulus correctly because the step after the first stim statement doesn't play all the stimuli before time is reset. The reason this is important is that typically in a sine wave stimulus each time step runs a intensity increment and an intensity decrement. If not all the intensity increments are run, invariably the last decrements are not added. The correct way to run a stimulus is:
TO = 1;
FRO = -1;
predur = .01; /* equilibration time before model runs */
time = 0 - predur; /* sets time negative to allow equilib. time */
setxmin = 0; /* sets x-axis beginning at time=0 */
sdur = 0.1;
durtotal = sdur + predur;
stim sine contrast 0.4 inten .01 tfreq 10 drift TO start time dur durtotal;
step durtotal; (correct)
time = 0;
stim sine contrast 0.4 inten .01 tfreq 10 drift FRO start time dur sdur;
step sdur;
Another way to use the simulator is to run the simulation time steps inside a loop in construction mode:
time_incr = timinc;
set_plots();
for (i=0; i<=ntrials; i++) {
time = 0;
set_stimuli();
for (t=0; t<=endexp; t+= time_incr) {
modify_circuit();
step time_incr;
};
};
This way allows you to modify the circuit each time step, for example, to continuously change the structure or function of the neural circuit. However, this method runs slower since construction mode runs interpreted line by line.
Each time the simulation is run with a "run" or "step" statement the time step cycles through simulation events in a certain order:
1) Stimuli
2) Synapses
3) Photoreceptors
4) Time integration in compartments
5) Onplot procedure
6) Plots
7) Time incremented to next step
This means, for example, that if you run a voltage clamp for 0.1 ms, and set up a voltage plot during runtime, and "step" to run the simulation, you will only record a current during the time the voltage clamp is on:
(interpreted:)
ploti=0.0001; /* set plot time increment */
at [0][0] cone (0,0);
at [0][0] sphere dia 1 rm=1000;
stim spot 10 loc(0,0) inten=1000 start 0 dur .0001;
stim node [0][0] vclamp -.01 start 0 dur .0001;
plot V[0][0]; /* run-time plots */
plot I[0][0];
plot L[0][0];
step 0.0002;
(compiled:)
ploti=0.0001; /* set plot time increment */
c = make_cone(nd(0,0), dia=1); c->xloc=0; c->yloc=0;
s = make_sphere(nd(0,0), dia=1, rm=1000);
stim_spot(10, 0, 0, inten=1000, start=0, dur=0.0001);
vclamp(ndn(0,0),clamp=-0.01, start=0, dur=0.0001);
plot (V,ndn(0,0)); /* run-time plots */
plot (I,ndn(0,0));
plot (L,ndn(0,0));
step (0.0002);
If you would like to record the current at the end of the voltage
clamp time, you can stop "run" mode by limiting the step
statement to the duration of the voltage clamp. Then you can
record the final values of any of the parameters of the
simulation since stopping "run" mode stops simulation time from
running forward:
(interpreted:)
at [0][0] cone (0,0);
at [0][0] sphere dia 1 rm=1000;
stim spot 10 loc(0,0) inten=1000 start 0 dur .0001;
stim node [0][0] vclamp -.01 start 0 dur .0001;
step .0001;
print "time",time, "V",V[0][0], "I",I[0][0]; /* construction-mode plot */
(compiled:)
c = make_cone(nd(0,0), dia=1); c->xloc=0; c->yloc=0;
s = make_sphere(nd(0,0), dia=1, rm=1000);
stim_spot(10, 0, 0, inten=1000, start=0, dur=0.0001);
vclamp(ndn(0,0),clamp=-0.01, start=0, dur=0.0001);
step (0.0001);
printf ("time %g V %g I %g\n",time,v(nd(0,0)),i(nd(0,0)));
The result of the translation at run-time is a set of linked lists of compartments, connections and pointers between them which the computer scans at high speed for every time step of the simulation run. Each compartment has a linked list of pointers (no limit on the number) which define its connections. Each connection has a set of pointers to the compartments it connects. Every type of connection to a compartment has its own set of mathematical instructions that describe the voltage and current flow through the connection.
NeuronC defines several types of neural elements. Each element connects to either 1 or 2 nodes, and the nodes must be given when the element is defined. The types are:
Type Nodes Description cable 2 defines multiple compartments. sphere 1 defines one compartment. synapse 2 defines connection between 2 nodes. gap junc 2 defines resistive connection between 2 nodes. rod,cone 1 transduction apparatus connected to node. transducer 1 voltage clamp controlled by light itransducer 1 current clamp controlled by light vbuf 2 buffer (voltage follower). load 1 resistor to ground. resistor 2 defines resistive conn. between 2 nodes (same as g.j.) electrode 2 defines resistive conn. between 2 nodes and cap at first cap 2 series capacitor between 2 nodes. gndcap 1 capacitor to ground; adds capacitance to node. batt 2 series battery between 2 nodes. gndbatt 1 battery to ground. chan 1 active set of channels in membrane.
It is often useful to change the default value of a parameter that you have defined in your script. You can do this with the "setvar()" function, which sets variables in your script from values you give on the command line with the "-s variable xx" option (see Setting variables from command line below).
The syntax for the neural elements is given below. Extra spaces (not needed for separating words) are ignored, as are newlines (line feeds or the "enter" key). Words not inside angle brackets must be spelled exactly. The angle brackets indicate a category of input, for example, "<expr> means an expression:
Symbol What to type in:
word Must be spelled exactly.
<expr> Expression needed here.
| Logical OR (either this stmt or another).
'word' Optional part of statement.
<node> Node number, either simple expression,
or a 1- 2- 3- or 4-dimensional number
inside square brackets (see below).
Can also include "loc" statement (see below).
Each element has either "conn" or "at" as its
required first word, followed by node expressions:
(interpeted:)
at <expr>
conn <expr> to <expr>
(compiled:)
at (nd(<expr>), <elemtype>);
conn (nd(<expr>), nd(<expr>), <elemtype>);
In the compiled version, nodes are defined using the "nd()" function call, listed in "ncfuncs.h". This call returns a pointer to the node and if necessary creates a node. A similar function, "ndn()" retrieves a node pointer if possible, but does not create a new node. These two functions require that the specfied node exist or return a NULL to indicate when it is not found. A third function "ndt()" allows specifying a node number without actually requiring that the node exist. This third form is used in the "display" statement (see below).
Node numbers can also be 2-, 3- or 4-dimensional, but in this case the node numbers must be enclosed with 2 or 3 sets of square brackets "[]"; for example:
(interpeted:)
at [<expr>][<expr>][<expr>]
conn [<expr>][<expr>][<expr>] to [<expr>][<expr>]
(compiled:)
at (nd(<expr>,<expr>,<expr>), <elemtype>);
conn (nd(<expr>,<expr>,<expr>), nd(<expr>,<expr>), <elemtype>);
Since the node number may be specified either as a simple
expression or as a 2-, 3- or 4-dimensional number inside square
brackets, node numbers in this manual appear like this:
(interpeted:)
at <node>
conn <node> to <node>
(compiled:)
at(<node>, <elemtype>);
conn(<node>, <node>, <elemtype>);
Three- and four-dimensional node numbers are useful for
specifying which presynaptic cells should connect to a post-
synaptic cell. To design your circuit this way, you can specify
connections to a neuron based on its type and cell number,
without explicitly keeping track of the total number of nodes or
compartments defined (which in many cases is a distraction) . To
do this, assign the first node dimension to mean "neuron type",
the second dimension to mean "cell number", and the third
dimension to mean "node number within the cell". If you have an
array of cells, you can assign a 2-dimensional "cell number"
(dimensions 2 and 3), leaving the fourth to describe the "node
within the cell".
(interpeted:) at <node> loc (<expr>,<expr>)However, locations of both nodes need not be defined in every "cable" statement. It is unnecessary to define the location of a node more than once. For example, if you are defining a cable with several segments, you can define the locations this way:conn <node> loc (<expr>,<expr>) to <node> loc (<expr>,<expr>) (compiled:) at ( loc (<node>, <expr>, <expr>), <elemtype>); conn(loc (<node>, <expr>, <expr>), loc(<node>, <expr>, <expr>), <elemtype>);
(interpeted:) connor:loc (10,0) to conn loc (20,0) to (compiled:) conn(loc (<node1>, 10, 0), <node2>, <elemtype>); conn(loc (<node2>, 20, 0), <node3>, <elemtype>);
(interpeted:)
for (i=0; i<10; i++) {
conn [i] loc (i*10,0) to [i+1]
};
(compiled:)
for (i=0; i<10; i++) {
conn(loc (nd(i), i*10, 0), nd(i+1), <elemtype>);
}
Also, the node locations may be specified in a
"dummy" definition statement:
(interpeted:)
at <node> loc (<expr>,<expr>)
(compiled:)
at (loc (<node>, <expr>, <expr>));
This defines no neural elements but defines the node and sets
the node's location. This method is useful when you have a list
of cables with absolute locations. In this case, you can specify
the locations of the nodes all at once, and then define the cables
and their diameters. The lengths are then determined
automatically from the node locations.
Photoreceptors are required to have a location in their definition (see "photoreceptors" below). But the photoreceptor location is for the purpose of light stimuli only.
(interpeted:)
seglen = 50;
conn <node> to <node> cable length=seglen rm=9500;
is equivalent to:
conn <node> to <node> cable length 50 rm 9500;
(compiled:)
seglen = 50;
c = conn(nd(<node>), nd(<node>), CABLE);
c->length=seglen; c->Rm = 9500;
is equivalent to:
c = make_cable(nd(<node>), nd(<node>));
c->length=seglen; c->Rm=9500;
Whenever an optional parameter is not specified, its
corresponding default value is used instead. Default values are
listed in Section 7, "Predefined variables". Setting an optional
variable does not change the value of its default. An attempt to
set a variable other than one of the valid parameters inside a
neural element statement will be trapped as an error.
To find errors, run NeuronC in "text mode" for printing the errors on the screen:
nc -t file
This prints out the graph commands as a set of
numbers on the screen, instead of graphics. If an
error is discovered, the line number and position of
the error on the line are printed, too. See section 5
for more information about how to run NeuronC.
(interpeted:)
conn <node> to <node> cable dia <expr> 'parameters'
(compiled:)
make_cable(nd(<node>), nd(<node>)); 'parameter code'
optional parameters:
--------------------------------------------------------------------------
dia = <expr> [ note that these "cable" params must come first ]
dia2 = <expr>
length = <expr>
cplam = <expr>
rm = <expr> [ "membrane" params, come after any "cable" params ]
ri = <expr>
cm = <expr>
vrev = <expr>
vrest = <expr>
jnoise = <expr>
rsd = <expr>
(interpeted:)
Na type <expr> 'vrev=<expr> 'density=<expr> 'offset=<expr>' 'tau=<expr>'
K type <expr> 'vrev=<expr> 'density=<expr> 'offset=<expr>' 'tau=<expr>'
KCa type <expr> 'vrev=<expr> 'density=<expr> 'offset=<expr>' 'tau=<expr>'
cGMP type <expr> 'vrev=<expr> 'density=<expr> 'offset=<expr>' 'tau=<expr>'
Ca type <expr> 'vrev=<expr> 'density=<expr> 'offset=<expr>' 'tau=<expr>'
(compiled:)
a = make_chan(<elem>, Na, na_type); 'a->vrev=<expr>' 'a->density=<expr>' 'a->voffsetm=<expr>' 'a->tau=<expr>'
a = make_chan(<elem>, K, k_type); 'a->vrev=<expr>' 'a->density=<expr>' 'a->voffsetm=<expr>' 'a->tau=<expr>'
a = make_chan(<elem>, KCa, kca_type); 'a->vrev=<expr>' 'a->density=<expr>' 'a->voffsetm=<expr>' 'a->tau=<expr>'
a = make_chan(<elem>, cGMP, cgmp_type);'a->vrev=<expr>' 'a->density=<expr>' 'a->voffsetm=<expr>' 'a->tau=<expr>'
a = make_chan(<elem>, Ca, ca_type); 'a->vrev=<expr>' 'a->density=<expr>' 'a->voffsetm=<expr>' 'a->tau=<expr>'
Where: <elem> is the cable or sphere element.
where:
parm: default: meaning:
-------------------------------------------------------------
length um (def by "loc()") length of cable segment
dia 1 um diameter of cable segment (= "dia1")
dia2 um defines taper, along with "dia1" (optional)
cplam 0.1 (complam) fraction of lambda per compartment.
rm 40000 Ohm-cm2 (drm) membrane leakage resistance.
ri 200 Ohm-cm (dri) axial cytoplasmic resistivity.
cm 1e-6 F/cm2 (dcm) membrane capacitance.
vrev -.07 V (vcl) battery voltage for leakage cond.
vrest -.07 V (vrev) initial startup voltage for cable seg.
jnoise 0 (off) (djnoise) Johnson noise in membrane resistance
rsd set by rseed random seed for Johnson noise
density .25 S/cm2 (dnadens) density of channel in membrane.
.07 S/cm2 (dkdens)
.005 S/cm2 (dcadens)
ndensity 10-30/um2 numeric density of channels in membrane.
(interpreted:)
Na type n 'vrev <expr>' 'density <expr>' 'thresh <expr> 'tau <expr>'
K type n 'vrev <expr>' 'density <expr>' 'thresh <expr> 'tau <expr>'
KCa type n 'vrev <expr>' 'density <expr>' 'thresh <expr> 'tau <expr>'
CGMP type n 'vrev <expr>' 'density <expr>' 'thresh <expr> 'tau <expr>'
Ca type n 'vrev <expr>' 'density <expr>' 'thresh <expr>' 'tau <expr>'
(compiled:)
a = make_chan(<elem>, Na, na_type); 'a->vrev=<expr>' 'a->ndensity=<expr>' 'a->voffsetm=<expr>' 'a->voffseth=<expr>' 'a->tau=<expr>'
a = make_chan(<elem>, K, k_type); 'a->vrev=<expr>' 'a->ndensity=<expr>' 'a->voffsetm=<expr>' 'a->voffseth=<expr>' 'a->tau=<expr>'
= additional voltage-sensitive macroscopic channel
conductance in cable membrane.
Vrev and density both have default values
appropriate for their channel types.
Type 0 channels are the HH type and are
taken from Hodkgin and Huxley, 1952.
Type 1 channels are the exact sequential
state equivalent to the type 0 channels.
See the "chan" statement below for a more
complete description. Channel densities can
be specificed as a conductance density or
a numeric density. A numeric density is
preferred to allow the temperature
dependence (Q10) to function correctly.
density .07 S/cm2 (dna) = density of channel conductance membrane.
ndensity 10 chan/um2 = typical numeric density of channels.
A "cable" statement defines a cable segment, normally used to construct the dendritic tree or axon of a neuron. At runtime, the cable is broken up into compartments, each with the length of the cable's "space constant" multiplied by the value of the parameter "cplam" (default set by the variable "complam", initally 0.1. See "predefined variables"). If the parameter "length" is not specified, the length of the cable is calculated as the distance between the two nodes at the cable ends, minus the radius of any spheres connected to those nodes. For this to work properly you must define the (x,y) or (x,y,z) locations of the nodes. If you specify the cable length, the subtraction of sphere radius at either end is not performed. The specified length may be different than the distance between the location of its ends. To define taper in a cable, you can specify the diameter at both ends with "dia1" and "dia2". If "dia2" isn't specified, the cable is not tapered. Any "cable" params (length, dia, dia2, cplam) must be specified before you specify any membrane parameters.
Each compartment consists of a chunk of membrane, which defines capacitance and leakage values, and internal cytoplasm, which defines axial resistance. A string of connected compartments is created automatically from the cable. The compartments are equal in size except for the two end compartments, which are 1/2 the size of the others. Each compartment is connected to its neighbors with resistors defined by the axial resistances. The membrane capacitance and resistance assigned to the end compartments are added to the capacitance and resistance values of the existing compartments defined for the cable's 2 nodes. If these compartments do not exist yet, they are created new.
You can set the membrane resistance and axial conductance for a cable to be sensitive to temperature using "dqrm" and "dqri". See "Temperature Dependence" below.
noise (std. deviation) = sqrt(4kTBG)
Where:
k = Boltzmann's constant
T = temperature (deg K)
B = bandwidth (set to inverse timinc)
G = membrane conductance in compartment
To turn on Johnson noise in all compartments, set the global
variable "djnoise". Its value is a multiplier for the basal level
of noise, i.e. jnoise=10 gives a standard deviation 10 times
higher than normal. Each compartment has its own individual
random number generator for Johnson noise so turning on "jnoise"
does not affect the random sequence of other noise sources.Note that the amplitude of Johnson noise in a compartment is dependent on the total conductance in the compartment, including all channels and synapses.
node1 <----------- cable1 ----------> node2 (nodes)
^ ^
comp1 - comp2 - comp3 - ... compN-1 - compN (compartments)
1/2 1 1 1 1/2 (comp. sizes)
these
comps
add
(nodes) node2 <------ cable2 --- > node3
^ ^
(compartments) comp21 - comp22 - comp23 - ...comp2N
(comp. sizes) 1/2 1 1 1/2
(interpreted:) at <node> sphere dia <expr> 'params' (same params as cable) (compiled:) at (nd(<node>), SPHERE); 'param code' (same params as cable) make_sphere (nd(<node>),dia=<expr>); 'param code' (same as cable)
The "sphere" statement defines an isopotential sphere, normally used for the soma or axon terminal of a neuron, that has membrane capacitance and leakage resistance but no internal resistance. Thus it is basically a shunting impedance. The values of resistance and capacitance are derived from the surface area of the sphere and the appropriate definition of membrane capacitance and resistance (default or specified). A sphere connects to 1 node, thus the resistance and capacitance are added to the compartment defined for the node. Macroscopic channel conductances are available for spheres just as for cables.
(interpreted:)
conn <node> to <node> synapse 'parameters'
(compiled:)
conn (nd(<node>), nd(<node>), SYNAPSE) 'parameters'
make_synpse (nd(<node>), nd(<node>)) 'parameter code'
optional parameters: default: meaning:
--------------------------------------------------------
open | close open Neurotrans opens or closes chans.
linear = <expr> | expon can be either linear or expon
expon = <expr> 5 mv exponential const (1/b) (mvolt)
vrev = <expr> -.00 V (vna, vk) reversal pot. (battery) (Volts)
thresh = <expr> -.05 V (dst) threshold for transfer (Volts)
sens = V | Ca V vesicle release sensitivity (set Ca <expr> for Ca sens)
vgain = <expr> 1 (dvg) vesicle release gain (linear multiplier)
mirpool= <expr> 1 (dsmirp) maximum intermediate releasible pool (when==1, off)
mrrpool= <expr> 50 (dsmrrp) maximum readily releasible pool
rrpoolg= <expr> 0 (dsrrg) release gain mul 0->conrolled by rrpool, 1->constant
maxsrate=<expr> 0 (dsms) maximum sustainable rate (ves/sec, default 0=>off)
cgain = <expr> 1 (dsc) synaptic cGMP gain (after sat.)
chc = <expr> 1 (dchc) Hill coeff for cGMP binding
nfilt1 = <expr> 2 (dsfa) number of presynaptic filters.
timec1 = <expr> 0.2 msec (dfta) synaptic low pass filter (msec).
timec1h= <expr> 1 msec (dftah) synaptic high pass filter (msec).
nfilt1h= <expr> 0 no. of presyn. high pass filters.
hgain = <expr> 0 gain of high pass filter ( < 0 => rel gain)
nfilt2 = <expr> 1 (dsfa) no. of filters after nt release.
timec2 = <expr> 0.2 msec (dfta) synaptic low pass filter (msec).
tfall2 = <expr> timec2 tau for falling phase (msec).
nfilt3 = <expr> 0 no. of filts for cond. after binding.
timec3 = <expr> 0 msec conductance low pass filter (msec).
tfall3 = <expr> timec3 tau for falling phase (msec).
kd = <expr> 1 (dskd) saturation point: cond/(cond+kd)
hcof = <expr> 1 (dshc) Hill coefficient: cond^h/(cond^h+kd^h)
trconc = <expr> 1e-4 M (dstr) Transmitter conc factor for AMPA, etc.(Molar)
mesgconc = <expr> 1e-5 M (dsmsgc) Transmitter conc factor for CGMP, etc.(Molar)
maxcond= <expr> 200e-12 S(dmaxsyn) Conductance when chans fully open (Siemens)
mesgout cAMP synapse controls local cAMP level.
mesgout cGMP synapse controls local cGMP level.
(interpreted:)
vesnoise = <expr> 0 (off) = 1 -> define vesicle noise
N = <expr> 5 (dsvn) number of vesicle release sites
vsize = <expr> 100 (dvsz) size of vesicles released
vcov = <expr> 0 stdev/mean of vesicle size
rsd = <expr> set by rseed,srseed random seed
CoV = <expr> Poisson mult * stdev / mean ves rate
refr = <expr> 0 sec minimum time betw vesicle release
resp Postsyn sequential-state receptors.
AMPA AMPA receptor possibly with desensitization, Ca permeability.
ACH ACH receptor with Ca permeability.
NMDA NMDA receptor with voltage-sens.
GABA GABA receptor.
cGMP cGMP receptor.
SYN2 Simple 2-state channel.
<chanparm> = <expr> "vrev", "offsetm/h", "taum/h", "chnoise", etc.
(params taken from "channel")
chnoise = <expr> 0 (off) = 1 -> define chan noise (after "resp")
N = <expr> 100 (dscn) number of channels
unit = <expr> 50e-12 (dscu) unitary channel conductance
tauf = <expr> 1 (dsyntau) rel. time const for noise (abs=.001)
rsd = <expr> set by rseed,srseed random seed
(compiled:)
n = make_vesnoise(epnt); n->N=<expr>; n->vsize=<expr>; ...
c = make_chan(epnt, chantype, stype); c->maxcond=<expr>; n->unit=<expr>; ...
n = make_chnoise(epnt); n->N=<expr>; n->vsize=<expr>; ...
(See "ncelem.h" for synapse, channel and noise parameter definitions.)

Synaptic gain is specified by the value of the "linear" parameter. When set to 1.0, the neurotransmitter released is 1 for a presynaptic voltage of 100 mv above threshold. This value of Trel=1 half-saturates the saturation function (see below). For voltages less than the threshold, no transmitter is released. Larger values reduce the range over which the input voltage operates, i.e. a value of 2 increases the synaptic gain so that 50 mv above threshold releases transmitter of 1.
Trel = 0.01 * (Vpre - Vthresh) * gain * vgain (1)
where:
Trel = transmitter released to postsynaptic receptor.
(limited to be non-negative)
Vpre = presynaptic voltage (normalized to mv).
Vthresh = synaptic threshold (normalized to mv).
gain,vgain = linear transfer gain.
The transfer function may also be exponential, defined by the equation
Trel = .025 * e(Vpre-Vthresh) * vgain /expon (2)
where:
Trel = transmitter released, delayed to postsynaptic receptor.
Vpre = presynaptic voltage (mv).
Vthresh = synaptic threshold (mv).
expon = constant defining mvolts per e-fold increase (1/b).
vgain = linear transfer gain.
Reference: Belgum and Copenhagen, 1988
For exponential transfer, the transmitter released is
equal to the exponential function of the presynaptic voltage
above threshold. The value of "expon" sets how many
millivolts cause an e-fold increase in transmitter release.
Exponential release implies a gradual increase with voltage,
and it also implies that release is gradually shut off below
the threshold voltage. A synapse with exponential release
may require a presynaptic voltage 10 to 20 mv. below
threshold to extinguish transmitter release.
Note that "Trel", the signal representing released neurotransmitter, normally ranges from 0 to 1, or greater for saturation (maximum=1000). These values are "normalized" so that a value of Trel=1, when passed through the saturation function 5) below, causes a conductance of 0.5 of the maximum conductance ("maxcond"). Thus a value of Trel=5 is necessary to reach 80% of the maximum conductance.
The "vgain" parameter sets the proportion of neurotransmitter released. It is useful for keeping the vesicle release rate constant when you change the vesicle size (which otherwise modulates both size and rate). If you change the "vsize" parameter and the "vgain" parameter proportionately, the rate stays unchanged. If you change "vgain" alone, only the rate changes.
With "sens Ca <expr>", the amount of neurotransmitter released is the calcium concentration multiplied by the "sens Ca" value, multplied by a constant ("dscavg", default = 1e6), raised to a power function (default power=1), multiplied by the linear "vgain" parameter (default=1):
(interpreted:)
synapse ... sens Ca <expr> ...
(compiled:)
synapse *spnt;
spnt->casens = <expr>;
in the synapse code:
Trel = exp ( log([Ca]i * casens * dscavg) * caegain) * vgain
Where: casens is an individual Ca sensitivity for each synapse
dscavg is a constant (default 1e6);
caegain is the power (default=1)
vgain is a linear multiplier gain (default=1)
To set a cooperative effect of [Ca]i, you can set caegain to
a non-zero value. For example, a value of caegain=2 will simulate
two calcium binding sites on the release mechanism.
Click here to return to Synapse statement index
Each filter (from 1 to 4) is represented by the following equation:
Each stage is described by:
Vout (t+1) = Vout (t) + (Vin (t) - Vout(t)) * (1 - exp(-1/tau))
where:
Vout = output of delay filter.
Vin = input to filter.
t = time in increments of basic timestep
tau = time constant of filter (timec1) in increments of timestep.
This equation gives the behavior that one would expect from a filter with a time constant of "tau". The form of the equation corrects a discretization error that occurs with short time constants.
To minimize the lowpass filter effect of this function, use a short time constant. To maximize delay use all 4 filters. Total time delay is approximately equal to the sum of the individual time constants. The default setting is 2 filters with 0.2 msec time constants. If the time step is 1 sec. or greater, then the low-pass filter is removed and the synapse becomes a static transfer function.The signal that passes through the presynaptic delay function represents the steps that lead to transmitter release such as calcium entry and vesicle fusion. The signal that is actually filtered in this function represents the voltage above threshold, and so may range from -100 mV to 100 mV. The static release function 2) below converts this voltage into transmitter released. The signal values in the presynaptic filters may be recorded using the "FA0-4" notation (see "record").
It is possible to set several different time constants in any of the filters, with a different form of the "timec" parameter, for example, for 2 5-msec delays and 1 2-msec delay:
timec1 [5 5 1]
Defaults
The presynaptic delay function is set by default to 2 filters of 0.2 msec time constant. If the time step is 1 sec. or greater, then the low-pass filter is removed and the synapse becomes a static transfer function.
conn 1 to 2 synapse ...
synaptau = .01;
step .05; ( set 50 msec for equilibration )
synaptau = 1;
run;
Click here to return to Synapse statement index
When the rate of neurotransmitter vesicle release at a synapse is fast, that depletes the pool of presynaptic vesicles, which in turn limits the rate of vesicle release. The ability to release vesicles is regulated by the number of vesicles that are near to the synaptic release site and available for being docked, ready for membrane fusion. The group of vesicles available for immediate release is described as the "readily releasible pool." At a ribbon synapse (e.g. in retinal photoreceptors and bipolar cells, or auditory nerve) vesicles are tethered to the ribbon, which allows them to move faster to the release site. The readily releasable pool is the group of tethered vesicles that are closest to the cell membrane, ready for docking and release. The tethered vesicles farther away from the membrane are considered to be the "intermediate releasable pool." Other vesicles not yet tethered are the "reserve pool." The pools are continually repleted by endocytosis of old vesicles and also by creation of new ones. New vesicles are first transferred to the "reserve pool" and then to the "intermediate releasable pool" (irpool), which reloads the readily releasable pool. The rate of vesicle creation and refilling the rrpool and/or irpool is set by the "maxsrate" parameter.
This behavior is simulated by a first-order differential equation in which pool size controls the rate of release:
if (mirpool < 2) srate = maxsrate
else srate is defined by irpool (see "Intermediate releasable pool" below)
drrpool = srate * timinc * (1.0 - rrpool/mrrpool)
rrpool += drrpool
trel = rand(rrpool)
vesrel = trel * (rrpoolg + (1-rrpoolg) * rrpool / mrrpool)
rrpool -= vesrel
where:
rrpool = "readily releasable pool" of vesicles (with or without vesicle noise).
mrrpool = maximum size of readily releasible pool, defined by user, default "msrrp" = 50).
mirpool = maximum size of intermediate releasable pool (default: msirp = 1, don't use irpool)
maxsrate = maximum "sustainable release rate", defined by user.
srate = actual fill rate, set either to maxsrate or from irpool if used.
timinc = synaptic time step.
trel = neurotransmitter release available, i.e. before this computation.
vesrel = actual neurotransmitter released.
rrpoolg = gain for rrpool release, 1-> regulated by rrpool, 0-> constant gain
To simulate the "readily releasible pool", you can set the "mrrpool" and
"maxsrate" parameters. The "mrrpool" parameter (default=dsmrrp) sets the maximum
size of the readily releasibile pool, and the "maxsrate" parameter
(default=dsms) sets the "maximum sustained rate", i.e. the rate at which the
readily releasible pool is refilled. The rrpoolg parameter sets to what extent
the readily releasable pool's filled fraction controls release. For a rrpoolg =
0, the gain is controlled by the size of the readily releasable pool. For a
rrpoolg = 1, the gain is constant. In either case, the release rate is
controlled by the voltage gain (sometimes set by [Ca]i). Of course, in any
case, the readily releasable pool cannot release more vesicles than it contains
which is an upper limit on the synaptic transient gain.
When synaptic vesicle noise is activated (see below), replenishment of the readily releasible pool is stochastic, but has the same average rate (defined by maxsrate) as without synaptic vesicle noise. The actual number of vesicles released in a certain time interval will not be exactly proportional to the release rate, because the release of vesicles is stochastic. Moreover, variability in vesicle size can also be set (see below) which is a third source of vesicle noise.
By default the "maxsrate" parameter is set to 100/sec.
irpool += maxsrate * timinc * (1 - irpool/mirpool)
srate = trel * (rrpoolg + (1-rrpoolg) * irpool / mirpool)
irpool -= drrpool;
3) Click here to return to Synapse statement index
Vesicle noise (fluctuation of vesicle release) is set by one parameter, the size of a vesicle (size). The number of vesicles released is a random function (poisson distribution) of the release rate. Quantal release probability is calculated with the following equations:
n = Trel / size
q = poisdev(n)
Tnoise = q * size
where:
p = probability of release.
Trel = transmitter released (amount / 100 usec timestep; 1=half-sat).
size = size of release events (1=half saturating).
n = average (instantaneous) number of vesicles per time step.
q = number of quantal vesicles released per time step.
binom = random binomial deviation funtion of p, n.
Tnoise = transmitter released (Trel) with noise.
Reference: Korn, et al., 1982.
For a given amount of transmitter released (Trel) (and therefore
a given postsynaptic conductance) the "size" parameter affects the
size of quantal vesicles released. A higher value of "size" means
a lower probability of a vesicle being released per time step
which implies fewer quantal vesicles released and but larger
vesicle size. Changing "size" does not change the average amount
of transmitter released. The only other parameters affected by
"size" are vesicle rate and "amount" of noise.
The "size" parameter sets the amount of neurotransmitter in a vesicle released in a 100 usec timestep (the timestep used in calculating synaptic noise). Normally one doesn't want a vesicle's effect to disappear so quickly so one sets the vesicle duration by setting the time constant of the filter between neurotransmitter release and saturation (i.e. the "second" filter).
When setting "size", remember that a vesicle size of 1 means a the vesicle will produce a 1/2 max. conductance for a 100 usec timestep if there is no low-pass filter activated. When a low- pass filter is activated (nfilt2,timec2), the "energy" of the vesicle is maintained, i.e. its duration is increased and its amplitude is decreased. If you want to set the size of the vesicle after filtering, multiply the "size" by the time constant of the filter in 100 usec steps. For example, a size of 100 is required to produce a 1/2 max conductance with a filter time constant of 10 msec (i.e. (10 msec)/(100 usec) = 100).
The instantaneous rate of neurotransmitter release is always a function of synaptic activation (i.e. presynaptic voltage and gain). Since the "size" parameter also affects the rate of release of vesicles, normally during the course of testing a simulation one chooses a "size" that gives correct vesicle release rate (i.e. rate at 1/2 max total conductance). To lower the release rate without changing the vesicle size, change the synaptic gain, with the "vgain" or "expon" parameters. This affects probability of release (and therefore postsynaptic conductance) but not vesicle size or the vesicle rate necessary to produce a 1/2 max conductance.
r = gaussdist() * vcov + 1
vol = r*r*r
size = vsize * vol
Where:
r = radius of vesicle.
vol = volume of vesicle.
vsize = vesicle size set by user.
gaussdist = stochastic Gaussian distribution function
with zero mean and unit standard deviation.
You can set vcov from almost no variability (vcov=.01) to very
large variability (vcov=.5). The higher values (above .2)
increase the mean value by 10-30%.If you want to fit data to the third-power Gaussian distribution function, use this PDF function as a start:
y = exp ( (x^(1/3) - m)^2 / (2 * r*r)) * x^(-2/3);
for a sixth-power rule, use:
y = exp ( (x^(1/6) - m)^2 / (2 * r*r)) * x^(-5/6);
Where:
y = histogram of distribution function.
x = quantal size.
m = mean of Gaussian.
r = standard deviation of Gaussian.
The "N" parameter describes the number of independent release
sites for the purpose of the noise computation but does not affect
conductance. The effect of varying N is noticeable only when the
probability of releasing a vesicle is high (i.e. when N is small
and Trel is high), and this normally happens only when the release
rate is higher than 1000/sec/synapse. The maximum rate of release
is set (internally by the simulator) to 10 vesicles/release
site/timestep (100 usec), a value that should never be reached in
practice. When release rates are lower than this (the usual case)
the timing of release is "Poisson", meaning that the standard
deviation of the rate (i.e. its "noise") is proportional to the
square root of the mean. When N is set to zero, noise
is turned off. Note that saturation can affect a noisy synaptic signal differently than one without noise: the high amplitude noise peaks may saturate and cause the signal mean to be lower than a similar synapse without noise. To minimize this effect, 1) add filters at stage 2 to reduce fluctuation noise, or 2) reduce the amount of saturation by decreasing gain and increasing synaptic conductance ("maxcond").
Click here to return to Synapse statement index
Note that the activity of multiple synapses with random noise will not affect each other's random sequence, even though their sequences are set from the main random sequence "rseed". If you want to change one synapse's sequence without changing any others, you can set the pseudo-random sequence for that each synapse with the "rsd" parameter. When set, the "rsd = <expr> parameter keeps the random noise sequence constant for the synapse. The vesicle and channel noises can be initialized separately. Any synapses (or vesicle or channel noise generators within any synapses) that are not initilized with "rsd" are set by the overall "rseed" random number seed.
In addition, the "srseed" variable ("stimulus rseed") modifies the random seed for synapses (and for photoreceptors). This is useful when you want to use the main "rseed" to construct a neural circuit, but you want to vary the synaptic noise random sequence for different stimuli, while keeping the neural circuit constant. The "srseed" variable is added to "rseed" when each synapse's random sequence is defined. Its default value is 0, and any other integer value will change the synaptic noise. A typical use is to set it to the contrast of the stimulus multiplied by 1000.
gorder = 1.0 / (CoV*CoV);The gamma order is a floating point value, so practically you can set the value of CoV to any positive number. The vesicle release rate is set by the simulator from the presynaptic voltage and the neurotransmitter release function, so you only control the relative "regularity" of release with CoV, not the absolute regularity, exact standard deviation, or mean rate. Note that release is more regular with higher rates.
The "refr" parameter is an alternate way to specify regularity in vesicle release. It is specified in seconds and if non-zero it causes an absolute refractory period to be set up so that no vesicles are released during that period after each vesicle event. This causes release at high rates to be more regular than at low rates. Note that release will stop if the refractory period is equal to the mean period between vesicle events.
Click here to return to Synapse statement index
The neurotransmitter signal is passed through a second delay function that represents the delay between release at the presynaptic membrane and binding at postsynaptic receptors. The function also slows the rate of rise and fall of neurotransmitter binding to the post- synaptic receptor. The function is identical to the first one described above: it consists of up to 4 variable "resistor-capacitor" filters in series. As in the first delay function, the filters may use the same time constant or can be set to different time constants. In addition, the last filter in the series has an optional falling phase time constant that allows the duration of neurotransmitter action to be prolonged. The last filter connects to the static saturation function, described in 5) below.
The signal that passes through the post-release delay function represents the "neurotransmitter" released by the presynaptic terminal. This signal normally ranges from 0 to 10, where a value of 1 is half-saturated (see "saturation" below). The signal values in the filters may be recorded using the "FB0-4" notation (see "record").When a Markov function is used instead of a saturation function, the signal in the post-release delay function is calibrated in "M" or "Molar", determined by the "trconc" parameter (set for the Markov function) multiplied times the normalized signal used in the post-release delay filter.
This delay function is useful for defining a delay that affects the properties of the (optional) vesicle noise. There are 3 parameters, the number of filters ("nfilt2"), the time constant for the filters ("timec2"), and the optional falling phase parameter ("tfall"). To minimize the lowpass filter effect of this function, use a short time constant. To maximize delay, use all 4 filters. To pass all frequencies but maximize delay, use a short time constant with all 4 filters.
Each filter (from 1 to 4) is represented by the following equation:
Tdel (t+1) = Tdel (t) + (Trel (t) - Tdel(t)) * (1-exp(-1/tau))where:
Tdel = output of delay filter.
Trel = input to filter.
t = time in increments of basic timestep
tau = time constant of filter (timec2) in increments of timestep.
Falling phase tau
To use the optional falling phase, set the "tfall" parameter to the time constant you want for neurotransmitter removal. This time constant replaces the falling phase time constant in the last filter and gives an exponential decay to neurotransmitter action.
Note: nonlinear interactions with delay function
Note that if the synapse is set up for substantial saturation, any low-pass "averaging" filtering action in the post-release filter function will interact with the saturation in a "non-intuitive" nonlinear fashion. For example, if the function is given 1 msec delay, a large presynaptic signal may cause the post-synaptic signal to rise quickly (because the initial rise to saturation happens in less than 1 msec) but to fall with 5-10 msec delay because the "averaged" filtered signal keeps the synapse saturated even while the neurotransmitter release is falling.
A similar action can happen when a Markov function is substituted for the saturation function. When the postsynaptic delay filter is set for substantial averaging, a high rate of neurotransmitter released can saturate the postsynaptic Markov function receptor, even when neurotransmitter release is falling.
Defaults
The postsynaptic delay function is set by default to 0 filters (no filter) with 0.2 msec time constant. If the time step is 1 sec. or greater, then the low-pass filter is removed and the synapse becomes a static transfer function.
Click here to return to Synapse statement index
Rbound = Tdel^h / (Tdel^h + kd^h) (3)
where:
Rbound = Fraction of receptors bound with transmitter.
Tdel = transmitter (delayed and filtered Trel).
kd = binding constant for synaptic saturation. (default = 1)
h = Hill coefficient, representing cooperativity.
The released transmitter, delayed and averaged, is
delivered to the saturation function which allows the
conductance of the postsynaptic membrane to be limited
to the maximum defined by the "maxcond" parameter. The
default value for the binding constant (kd) is 1, so
saturation occurs when the transmitter released is greater
than 1, defined in equations (1) and (2) above. With a synapse set to use the standard saturation function, saturation is dependent on both "gain" and "kd". To change the level of presynaptic voltage at which saturation occurs, increase "gain". For an exponential synapse, the saturation occurs at a presynaptic level dependent on "gain", "expon", and "kd".
When a Markov function is used instead of the standard saturation function, the "kd" parameter is not relevant and the amount of saturation is dependent only on the neurotransmitter release and the Markov function.
The Hill coefficient, defined by the "hcof" parameter, represents the number of molecules of neurotransmitter that must be bound to a receptor for it to be activated, and describes the "degree of cooperativity". A Hill coefficient greater than 1 gives the saturation curve an S-shape, which means a "toe" at low concentrations of neurotransmitter, and a steeper slope in the mid-portion of the curve. Typical Hill coefficients are 2 or 3, although commonly a non-integer Hill coefficient is reported when measured from a pharmacological preparation.
Click here to return to Synapse statement index
cGMP = (1 - Rbound * cgain) (5)
cGMP >= 0
Gpost = cGMP / (cGMP + ckd) * (1 + ckd) * maxcond
where
cGMP = the second messenger concentration
Gpost = postsynaptic conductance
ckd = saturation constant for the 2nd messenger
the default level of ckd is set by "dckd" (default 0.1)
If the neurotransmitter action at the synapse has been set to "close", the "cgain" parameter represents the biochemical gain that couples bound receptors to the closing of membrane channels. Amplification in the biochemical cascade after saturation (i.e. cgain > 0) reduces the effect of saturation near the point where all the channels are closed. Gain may be very high at such a synapse with modest values of cgain (e.g. voltage gain = 100). The intermediate parameter "cGMP" represents the level of second-messenger that binds to the membrane ion channel. Since in the "generic" synapse this is limited to a range of 0 to 1, Gpost is multiplied by the factor "(1 + ckd)" in equation (5) above to give a reasonable amount of saturation when ckd=0.1. Normally this default value for ckd should not be changed. Note that the value of "Gpost" above is limited to the range 0 to maxcond.
The default action for neurotransmitter in NeuronC is to open channels, but this may be explicitly stated with the keyword "open".
If a "resp cGMP" is added in the parameter list after the "synapse" keyword, a cGMP channel becomes the output for the synapse's action:
... synapse close maxcond=1e-9 resp cGMP chnoise=1
This would generate a synapse in which neurotransmitter
closed a cGMP channel through a second-messenger system,
with 40 channels having a unitary conductance of 25 pS
(default for cGMP). The description of the channel type
determines the properties of cGMP binding and channel opening.Click here to return to Synapse statement index
The signal that passes through the post-saturation delay function represents normalized conductance and ranges from 0 to 1. The signal values in the filters may be recorded using the "FC0-4" notation (see "record").
This delay function is useful for defining a delay that affects both (optional) vesicle noise and (optional) channel noise. There are 3 parameters, the number of filters ("nfilt3"), the time constant for the filters ("timec3"), and the optional falling phase parameter ("tfall"). To minimize the lowpass filter effect of this function, use a short time constant. To maximize delay, use all 4 filters.
Each filter (from 1 to 4) is represented by the following equation:
Gdel(t+1) = Gdel(t) + (Gi(t) - Gdel(t)) * (1-exp(-1/tau))where:
Gdel = output of delay filter, goes to "Reversal Potential" below.
Gi = input to filter, from Gpost above or previous filter.
t = time in increments of basic timestep
tau = time constant of filter (timec3) in increments of timestep
Falling phase tau
To use the optional falling phase, set the "tfall" parameter to the time constant you want for neurotransmitter removal. This time constant replaces the falling phase time constant in the last filter and gives an exponential decay to neurotransmitter action.
Defaults
The postsynaptic delay function is set by default to 0 filters (no filter). If the time step is 1 sec. or greater, then the low-pass filter is removed and the synapse becomes a static transfer function.
Click here to return to Synapse statement index

The discrete state Markov function for AMPA, NMDA, ACH, etc, channels is placed between neurotransmitter concentration (i.e. temporal filter 2) and channel opening. Calibration of the absolute concentration of neurotransmitter at the postsynaptic receptor is set by the "trconc" parameter. This allows changing the response amplitude and amount of saturation of the receptor. During the simulation, the actual concentration is computed by multiplying "trconc" by the output of the second temporal filter. The level of neurotransmitter bound to the receptor drives the Markov function through the rate constants which are functions of neurotransmitter. (In the NMDA receptor, they're also functions of voltage). Output from the Markov function drives the postsynaptic channels. When channel noise is added to a Markov channel, the kinetics of channel opening and closing are set by the Markov state transitions but can be tuned with the "taua-tauf" parameters (see below). The cGMP Markov function is placed after postsynaptic binding and the third temporal filter. Calibration of the second messenger concentration is set by the "mesgconc" parameter, similar to the "trconc" parameter.
When a channel type is not explicitly defined by the "resp" clause, the trconc parameter can be used in the same way as specified above to vary the amplitude of the response and the amount of saturation specified by "kd". In this case, the default value of trconc is still "dstr" (as defined above) but the multiplier value is trconc/dstr, i.e. it is by default 1.0.
Channel noise can be defined without the "resp" keyword. When this is done a "syn2" channel is created automatically. This example defines a synapse that opens a 2-state Markov channel with 20 channels (with a default unitary conductance of 25 pS):
... synapse ... open chnoise=1 N=20
The order of most synaptic parameters is arbitrary (you can specify them in any order) but any "resp" parameters to specify the postsynaptic channel should all be sequential, starting after "resp", i.e you should specify "resp" and then place all the "channel parameters" ("vrev", "offsetm/h", "taum/h", "caperm", etc.).
(interpreted:)
OK:
conn node1 to node2 synapse
presynaptic options...
;
OK:
conn node1 to node2 synapse
presynaptic options...
vesnoise options ....
;
OK:
conn node1 to node2 synapse
presynaptic options...
vesnoise options ....
chnoise options ...
;
OK:
conn node1 to node2 synapse
presynaptic options...
vesnoise options ....
resp AMPA taum=2
chnoise=1 unit=20e-12
;
OK:
conn node1 to node2 synapse
presynaptic options ...
vesnoise options ...
resp AMPA taum=2
caperm = .2
chnoise=1 unit=20e-12
;
Gives error message:
conn node1 to node2 synapse
presynaptic options ...
vesnoise options ...
caperm = .2 (caperm specified before "resp AMPA")
resp AMPA taum=2
chnoise=1 unit=20e-12
;
(compiled:)
synapse *s;
chattrib *c;
nattrib *n;
s = make_synpse (nd(node1), nd(node2))
presynaptic options: s->vrev=-0.045; s->thresh=-0.045; ...
vesnoise options: n = make_vesnoise(s); ...
postsynaptic options: c = make_chan(s, AMPA, 0); c->taum=2; c->maxcond = 100e-12; ...
chnoise options: n = make_chnoise(s); n->unit=20e-12;
Note that vesnoise, channel noise, and a channel attribute are optional.
If no channel is specified, generic postsynaptic binding/saturation and
conducance functions are created.
The "chnoise" parameter can be specified without "resp", i.e. you don't need to use the "resp" parameter if you only want to add noise. But in that case, a simple postsynaptic 2-state channel type will be created to allow the synapse to have noise properties.
Note that the "N" and "unit" parameters can be placed before, after, or without "chnoise". If placed before "chnoise", they define the conductance of the channel. If placed after chnoise, they define only the noise properties of the channel, not its conductance:
... synapse ... open N=20 chnoise=1
You can modify the behavior of the Markov functions with the
"tau" and "offset" parameters (similar to those in "channel"):
"offset" defines a voltage to be added to the membrane voltage
for the NMDA channel, and "tau" defines a multiplier for the time
constant functions (i.e. a divider for rate functions). You can
separately specify a relative "taum" (activation) and "tauh"
(inactivation) multiplier for some channels and "taua-tauf"
provide a way to tune 6 separate rate functions.Click here to return to Synapse statement index
The "unit" parameter describes the unitary conductance of a single channel and allows the simulator to calculate the number of channels from the maximum total conductance "maxcond". If you specify a value for "N", the value of "unit" is ignored, otherwise, the total number of channels is calculated as:
N = maxcond / unit
The "N" parameter describes the number of independent channels
for the purpose of the noise computation but does not affect
conductance. The instantaneous number of open channels is a random function
(binomial deviation) of the probability of each channel opening
and the number of channels.
Defaults for "unit" (the unitary conductance) are:
dscu = 25e-12 @22 default 2-state synaptic channel dampau=25e-12 @22 default AMPA unitary conductance dachu =80e-12 @22 default ACH unitary conductance dcgmpu=25e-12 @22 default cGMP unitary conductance dnau = 22e-12 @22 default Na unitary cond, gives 32 pS @33 deg (Lipton & Tauck, 1987) dku = 11.5e-12 @22 default K unitary conductance gives 15 pS @30 deg dkau = 22e-12 @22 default KA unitary conductance gives 30 pS @30 deg dkcabu= 74.3e-12 @22 default BKCa unitary cond, gives 115 pS @ 35 deg dkcasu= 14.2e-12 @22 default SKCa unitary cond, gives 22 pS @ 35 degNote that the default unitary conductances have a temperature coefficient, set by the Q10 for channel conductance "dqc" (default = 1.4). The base temperature at which the unitary conductance is defined is set by the "qt" field of the channel constants. For HH-type rate functions, the orginal temperature was 6.3 deg C, and these original equations are multiplied by a standard factor to normalize them to 22 deg C. For synapses it is also 22 deg C. For more details, look in "Adding New Channels".
You can change the default base temperature for unitary conductances (and kinetics) with the following variables:
var default meaning ------------------------------------------------------------------------------ dbasetc 22 deg C base temp for membrane channel kinetics, conductances dbasetsyn 22 deg C base temp for synaptic kinetics dbasetca 22 deg C base temp for ca pumps dbasetdc 22 deg C base temp for Ca diffusion constantClick here to return to Synapse statement index
The time constant controls the frequency spectrum of the channel noise. The default time constant for the "syn2" simple 2-state channel is 1 ms and this can be changed (multiplied) with the "tauf" parameter. The time constant defines a noise event with an average single exponential time course (single Lorenzian), whose "roll-off" frequency is:
fc = 1 / ( 2 * PI * tau)
The power spectral density at frequency = fc is half of
that at lower frequencies.See the description of vesicle noise above for a discussion of the random "seed" and how to change it.
Click here to return to Synapse statement index
Gpost = G * maxcond (4)
where:
Gpost = postsynaptic conductance.
G = Fraction of receptors bound, after saturation and noise.
maxcond = maximum postsynaptic conductance
(default = 1e-8 S)
The fraction receptor bound is always less than 1,
so the postsynaptic conductance can only approach the level
specified by "maxcond". The instantaneous conductance may
be recorded with the "G0" notation (see "record").Click here to return to Synapse statement index
The post-synaptic current reverses when the intracellular voltage passes above or below the synaptic battery potential; thus the name "reversal potential".
Ipost = (Vcell - Vrev) * Gdel
where:
Ipost = postsynaptic current
Vcell = intracellular voltage
Vrev = reversal (battery) voltage for synapse
Gdel = postsynaptic conductance, (Gpost delayed)
Click here to return to Synapse statement index
If you specify a cGMP-gated postsynaptic channel with the "resp" option it will automatically receive its signal from the synapse in the same manner as if you use the "mesgout" option and a separate "chan cGMP" statement.
Note that the third temporal filter can approximate the low-pass filtering action of a second-messenger without the need to specify one with the "mesgout" option (see "Postsynaptic delay function" above).
Click here to return to Synapse statement index
The "dyad" parameter allows you to connect 2 or more postsynaptic mechanisms to one presynaptic release mechanism. Photoreceptors and bipolar cells of the retina have such synapses, where the neurotransmitter from each vesicle is thought to diffuse to 2 sets of receptors each on a different postsynaptic neuron. The effect of this is to preserve the vesicle release timing in both postsynaptic cells.
To use the "dyad" parameter, you need to create one synapse first, and name it with the "ename" parameter. This stores the synapse's "element number" in the ename parameter (actually it's an ordinary variable that holds an integer number). Then you create a second synapse, but instead of specifying presynaptic parameters such as gain and release function, you specify "dyad name" where "name" is the variable that you set with the "ename" parameter from the first synapse:
(interpreted:)
conn 1 to 10 synapse open expon 5 /* first synapse */
thresh = -.045
maxcond=1e-10
timec2=2 nfilt2=2
ename syn1; /* save element number in "syn1" */
conn 2 to 10 synapse dyad syn1 /* second synapse, dyad to first */
maxcond=1e-10 /* only specify postsynaptic params */
timec3=10 nfilt3=2;
(compiled:)
int nfilt;
synapse *s;
s = make_synpse (nd(1), nd(10)); s->ntact=OPEN; s->ngain=5; /* first synapse */
s->thresh= -.045
s->maxcond=1e-10
s->timec2=2 nfilt2=2
nfilt=2; s->nfilt2 = (short int)nfilt;
s->timec2 = makfiltarr(nfilt,0,s->timec2,2);
syn1=spnt->elnum; /* save element number in "syn1" */
s = make_synpse (nd(2), nd(10)); s->ntact=DYAD; s->ngain=syn1; /* second synapse, dyad to first */
s->maxcond=1e-10;
nfilt=3; s->nfilt3=(short int)nfilt;
s->timec3 = makfiltarr(nfilt,0,s->timec3,10);
Note that for the second synapse (labeled "dyad"), you can only specify postsynaptic parameters such as filter 2, filter 3, saturation, conductance, and channel noise. You can also specify a Markov channel with "resp" (see above). Both postsynaptic cells will receive a signal whose envelope has identical timing, but they can have different conductances and channel noise.
Click here to return to Synapse statement indexThe "spost" parameter allows you to connect 2 or more presynaptic mechanisms to one postsynaptic release mechanism. It is thought that at some synpses the neurotransmitter can diffuse with enough concentration a few microns away that it can modulate other "extrasynaptic" ligand-binding sites. Photoreceptors are thought to have such synapses, where the neurotransmitter from the ribbon synapse (where neurotransmitter is released onto invaginating dendrites from horizontal and on-bipolar cells) is thought to diffuse to the "flat" contacts from off bipolar cells up to 3-5 microns away. Each vesicle is thought to diffuse to several sets of receptors each on a different postsynaptic neuron. The effect of this is to mix together the vesicle release timing from several release sites in one postsynaptic cell.
To use the "spost" parameter, you need to create one synapse first, and name it with the "ename" parameter. This stores the synapse's "element number" in the ename parameter (see "dyad" above). Then you create a second synapse, but instead of specifying postsynaptic parameters such as saturation, binding, and conductance, you specify "spost name" where "name" is the variable that you set with the "ename" parameter from the first synapse:
(interpreted:)
conn (1) to (10) synapse open /* first synapse */
expon 20 maxcond 200e-12
thresh -.04 timec1 .5
nfilt2=2 timec2 2 vgain=5
vesnoise=1 vsize=50
ename syn1; /* save element number in syn1 */
conn (2) to (10) synapse open /* second synapse, uses postsyn from first */
expon 20 /* only specify presynaptic params */
thresh= -.04 timec1=.5
nfilt2=2 timec2=2 vgain=5
vesnoise=1 vsize=50
spost syn1;
(compiled:)
See example of "dyad" for compiled above.
Note that for the second synapse (with the "spost" parameter), you can only specify presynaptic parameters such as expon (gain), conductance, thresh, etc. The second filter "filt2" for this purpose can be either presynaptic or postsynaptic, i.e. it can be used with either "dyad" or "spost" parameters.
You can use both "dyad" and "spost" at the same time to specify a situation where there are several presynaptic and postsynaptic mechanisms that share a common neurotransmitter pool.
Click here to return to Synapse statement indexTo specify a membrane channel type that is modulated by extra-synaptic neurotransmitter, as in a second-messenger system that modulates Ca++ or K+ channels from an mGluR2 or GABA-b receptor, you can call the "set2ndmsg()" function after the first "step" statement. You specify the channel type and subtype, and the presynaptic and postsynaptic cell types. A call to this function will then cause a synapse from any cell of the presynaptic type to any cell of the postsynaptic type, that uses the neurotransmitter specified, to modulate the channels on the postsynaptic cell, within the specified "active_radius".
set2ndmsg(chan_type, chan_subtype, presyn_celltype, postsyn_celltype, neurotrans, active_radius, gain); set2ndmsg(chan_type, chan_subtype, presyn_celltype, postsyn_celltype, neurotrans, active_radius, gain, tau);where:
chan_type type of channel (CA, K, NA, etc)
chan_subtype subtype of channel (-1 matches any subtype)
presyn_celltype presynaptic cell type (first dim of node number)
postsyn_celltype postsynaptic cell type (first dim of node number )
neurotrans neurotransmitter to activate 2nd mesng system (AMPA, GLU, GABA, etc)
active_radius how far way the channel can be from the synapse, in um
gain gain for modulating channel (1-10, etc, depending on code)
tau time constant (ms) for modulating channel (-1 sets default: 5 ms, set by dftm)
Example of use:
step (1e-4); // short step before run to create model with channels set2ndmsg(CA,-1,dbp1,sbac,AMPA,sb_mglur_maxdist,mglur2); // set glutamate to modulate Ca chans, default tau 5 msor, to set the time constant:
step (1e-4); // short step before run to create model with channels set2ndmsg(CA,-1,dbp1,sbac,AMPA,sb_mglur_maxdist,mglur2,100); // set glutamate to modulate Ca chans with 100 ms tauAt runtime, this function will set up a call to the "run2ndmsg()" function to modify the channel's conductance. At present this function is called only for CA and K channel types. To understand how the modulation affects the target channel, or if you want to add a new type of extra-synaptic modulation, see the "run2ndmsg()" function in nc/src/ncomp.cc. Click here to return to Synapse statement index
(interpreted:) conn <node> to <node> gj <expr> 'parameters' (compiled:) gapjunc *gj; gj *make_gj (nd(<expr<), nd(<expr<), <maxcond>); 'parameter code' ---------------------------------------------- parameters: units: default: meaning: gj <expr> S conductance of gap junction. area = <expr> um2 membrane area of gap junction (alt.). dia = <expr> um diameter of gap junc(alt. to area). rg = <expr> Ohm-um2 5e6 (drg) specific resistance of gj membrane. vgain = <expr> mV 1.0 mV per e-fold change in rate. offset= <expr> V 0.015 (dgjoff) offset voltage. taun = <expr> ratio 1.0 (dgjtau) divider for rate function. gmax = <expr> S conductance of gap junction. gnv = <expr> ratio 0.2 (dgjnv) non-voltage-sensitive fraction. rev 'params' rectifying params for neg voltage. mesgin cAMP modulation by cAMP at local node. mesgin cGMP modulation by cGMP at local node. mesgin cAMP <node> modulation by cAMP from remote node. mesgin cGMP <node> modulation by cGMP from remote node. mesgin 'params' open (close) cAMP/cGMP opens the gj channel. mesgin 'params' close (default) cAMP/cGMP closes the gj channel.A gap junction is implemented as a resistive connection between two nodes, much like the connection between compartments along the length of a cable. Its conductance can change as a function of the cross-junctional voltage. The change is small and slow in response to a voltage step of less than 10 mV, but increasingly strong and rapid above 15 mV. The maximum conductance can be defined immediately after the keyword "gj" (in Siemens), or alternately can be defined by its area, or diameter:
gmax = area / specific resistance gmax = PI*dia*dia/ (4 * specific resistance)To calibrate "area" as a conductance, set the specific resistance "rg" (or drg, its default) to 1. Then the value you supply after "area" is interpreted as the conductance in Siemens.
Optional parameters define the specific resistance, defined in units of ohm-um2 (default 5e6 ohm-um2), voltage gain ("vgain"), the number of mV per e-fold change in rate, and the time constant "taun", which changes the opening and closing rates proportionately. The opening and closing rates are also influenced by temperature (set by "tempcel") with a Q10 of 3, in a manner similar to other membrane channels (Hodgkin and Huxley, 1952). To disable the voltage sensitivity, set the Gmin/Gmax ratio ("gnv") to 1.0, or set its default ("dgjnv") to 1.0.
alpha = tempcoeff * taun * exp(-Aa * (vj - offset) / vgain);
beta = tempcoeff * taun * exp( Ab * (vj - offset) / vgain);
n += -beta * n + alpha * (1.0 - n) * t;
Ggj = (gnv + n * (1.0-gnv)) * (1.0-cyc)
Where: tempcoeff = temperature coefficient determined by Q10 of 3.
Aa = power coefficient for alpha, set to 0.077
Ab = power coefficient for beta, set to 0.14
t = time increment for synapses (always 100 usec).
n = normalized voltage-gated conductance from 0 to 1.0.
gnv = non-voltage-gated fraction, from 0 to 1.0
cyc = level of cyclic nucleotide "second-messenger".
Ggj = normalized total gap junction conductance.
You can change the rate for opening and closing (alpha and beta)
by setting taun, offset, and vgain. Because offset and vgain
are within the exp() function, they have a larger effect when
the voltage is greater. Taun will linearly change the rate.For details on the voltage gating properties, see Harris, Spray, Bennett, J. Gen Physiol. 77:95-117, 1981.
The "reverse" parameters are vgain, offset, and taun. If any of these are set, the gap junction is effectively split in half with the forward parameters defined before the "rev" keyword, and the reverse parameters defined after the "rev" keyword. In this case, the reverse parameters are used when the voltage across the gap junction is negative. Defaults for the reverse parameters are specified by the forward ones.
The "cAMP" and "cGMP" parameters set modulation by these second- messengers. If no node is specified, the second-messenger levels at both nodes connected by the gap junction will influence the gap junction conductance. When a node is specified for the second messenger, the gap junction is modulated by second-messenger at only that single node.
Click here to return to NeuronC Statements
(interpreted:) at <node> rod (<xloc>,<yloc>) 'parameters' at <node> cone (<xloc>,<yloc>) 'parameters' at <node> chr (<xloc>,<yloc>) 'parameters' at <node> transducer (<xloc>,<yloc>) 'parameters' at <node> itransducer (<xloc>,<yloc>) 'parameters' (compiled:) photorec *p; p = make_rod (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>;'parameters' p = make_cone (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>;'parameters' p = make_chr (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>;'parameters' p = make_transducer (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>;'parameters' p = make_itransducer (nd(<node>));p->xloc=<xloc>; p->yloc=<yloc>;'parameters' p = make_rod (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>; p->stimchan=<expr>; p = make_cone (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>; p->stimchan=<expr>; p = make_chr (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>; p->stimchan=<expr>; p = make_transducer (nd(<node>)); p->xloc=<xloc>; p->yloc=<yloc>; p->stimchan=<expr>; p = make_itransducer (nd(<node>));p->xloc=<xloc>; p->yloc=<yloc>; p->stimchan=<expr>;optional parameters:
-----------------------------------
units: default:
<xloc>,<yloc> um location of receptor in (x,y) plane.
maxcond=<expr> S 1.4e-9 S dark cond of light-modulated channels.
dia = <expr> um 2 um dia of receptor used for phot. flux.
pigm = <expr> 1 0=rod, 1-3=cone l,m,s, default 1; see below for more
pathl = <expr> um 35 um path length for light through receptor
attf = <expr> .9 light attenuation factor (lens, etc.)
filt = <expr> 0 0=none; 1=macular pigm, 2=lens, 3=macular+lens,
4=lens, open pupil, 5= macular+lens, open pupil
timec1= <expr> 1.0 time constant multiplier.
loopg = <expr> 1.0 gain of ca feedback loop, sets stability
linit = <expr> ph/um2/sec 0.0 initial light value for equilibration
photnoise = <expr> 0 0->off; 1->on, Poisson photon noise from light flux.
darknoise = <expr> 0 0->off; 1->SNR=5; 0-10, ampl Gaussian cont noise.
stimchan = <expr> 0 private stimulus channel 0-9, (default 0=>none).
rsd = <expr> set by node # Individual random seed, -1 -> set by rseed
save save state variable values for later "restore"
restore restore values from previous "save"
A rod or cone photoreceptor is a transduction
mechanism which responds to light and modulates a
channel with certain gain, saturation, and time
properties. The channel is added (in parallel) to the
membrane properties for the compartment of the node
which the receptor connects. A "chr" photoreceptor
is a channel-rhodopsin which responds to light but
directly controls a membrane ion channel. Its "pigm"
parameter has a default of 25, the "ChR2" pigment.
A transducer photoreceptor converts a light stimulus directly into a voltage or current that it injects (through a voltage or current clamp) into the node's compartment. Otherwise it is similar to the rod and cone photoreceptors.
To stop the voltage clamp in a transducer, set the light intensity to a value less outside of the range of the variables "stimonh" and "stimonl" (default= 1, -1), which define the high and low values for a "stimulus-on" window. When the transducer sees a more positive value than "stimonl" and a more negative value than "stimonh", it activates the voltage clamp. For all other values, the voltage clamp is turned off, allowing the voltage to be controlled by other neural circuit elements. If the values are reversed, i.e. "stimonh" is more negative than or equal to "stimonl", the values describe a "stimulus-off" window, i.e. when the transducer sees a more positive value than "stimonh" and a value more negative than "stimonl", the voltage clamp is turned off.
An itransducer is similar to a transducer but converts the light intensity into a current that it injects into the node's compartment.
Click here to return to Photoreceptor statement index
Click here to return to Photoreceptor statement index
If you would prefer to set each noise generator, you
can independently set the pseudo-random sequence that each
photoreceptor receives with the "rsd" parameter. When set, the
"rsd =
Click here to return to Photoreceptor statement index
To specify a non-zero aperture for simulating low-pass
spatial filtering, you can add the effect of the aperture to
either the stimulus or the optical blur. For instance, if
you are using a point-source stimulus (with or without
blur), enlarging the point-source into a spot the size of
the photoreceptor aperture simulates the spatial-filtering
effect of the aperture in the photoreceptor. Alternately,
if the optical blur Gaussian is at least twice the diameter
(at 1/e) of the aperture, you can "pre-convolve" the optical
blur with the aperture. This can be accomplished using
either a separate convolution algorithm or the "root-mean-
square rule" for convolution of 2 Gaussians (the resulting
Gaussian diameter is the square root of the sum of the
squares of the two constituent Gaussian diameters).
Click here to return to Photoreceptor statement index
Example:
Note that the entire model including the photoreceptors
can be saved and restored using the "save model (
By varying the "timec1" parameter, you can run the
photoreceptor faster or slower. The photoreceptors are set by
default to have a time to peak appropriate for mammals, or about
200 msec for rods and 60 msec for cones. You can lengthen these
values to be appropriate for lower vertebrates (1 sec time to
peak for rods). Or you can shorten the time to peak, which is useful
to minimize the amount of computation in a simulation that
records the response to a quick flashed light stimulus. Sometimes,
waiting around for 100 msec to get the response seems wasteful.
Remember that membrane time constants will reduce the amplitude
of the quicker voltage response recorded inside a neuron.
By varying the "loopg" parameter, you can run the
photoreceptor calcium feedback loop with more or less gain. This
sets the conditional stability of the loop. The default value for
loopg is 1.0, which sets the Ca feedback loop a little unstable,
so that the response overshoots during recovery. This type of
behavior has been reported by Schneeweis & Schnapf (1999).
A value less than 1 will reduce the amount of overshoot.
The minimum value is 0.2, which causes a long recovery phase.
Photoreceptor light-modulated conductances are set with the
"maxcond" parameter. The total bound fraction is always less
than 1 so the maximum conductance is never exactly reached.
Actual rod and cone conductances are non-linear but they are
approximated by linear conductances in NeuronC. The rod
conductance is nearly a current source (Baylor and Nunn, 1986) so
that the light-modulated current is nearly constant over the
physiological range (-20 to -60 mv). Thus the rod reversal
potential is set to a large value (+720 mv). The cone
conductance is more linear (Attwell et al., 1982), and reversal
potential is predefined to be -8 mv. In order to give
physiologically correct intracellular voltages, the rod and cone
transduction mechanisms must be used with an appropriate leakage
conductance (see definition files "rod.m" and "cone.m").
The rod and cone receptors are similar but the rod is
approximately 100 times more sensitive. The rod mechanism
responds to 1 photon with a voltage bump of about 0.5 mv and the
cone mechanism responds to a 100 photon flash similarly. The
cone response also is somewhat faster (peak in 60 msec), and has
a negative undershoot on the recovery phase. New types of
photoreceptors can be created (using the same set of difference
equations) by adding a new set of "receptor constants" to the
subroutine "initrec()" in the file "ncmak.c" and recompiling.
You can plot the values in the transduction cascade with:
The macular pigment is a yellow filter that excludes
blue light from foveal cones, and the lens filter cuts off
sharply in violet. The macular+lens filter adds the filtering
properties of both filters in series (by adding their optical
densities). The transmission spectrum for these filters is
determined by table lookup, and the tables are from standard
references. See the source code in "ncstim.cc", "wave.cc",
"odconv.n", "macul.txt", and "lens.txt".
The turtle pigment sensitivity functions (pigm=4,5,6) are
narrower than the corresponding primate pigments because turtles
have colored oil droplets in the inner segment of the M and S
cones that selectively filter the light reaching the outer
segment. The turtle data are from Perlman, Itzhaki, Malik, and
Alpern (1994), Visual Neuroscience, 11:247, Figs.4, 10, as
digitized by Amermuller et al, Oldenburg, DE. The peaks were
modified for smoothness, and the curves extrapolated from 400 to
380 nm and from 700 to 800 nm. The longwave extrapolation was
done by the method of Lewis (1955) (J.Physiol 130:45) in which
the log(sens) of a visual pigment is linear when plotted against
wavenumber. (See "turtlesens.n" which was used to make
"turtle.h", which contains the log(sensitivity) functions
included in "wave.cc", which generates log(specific OD) functions
in "wave.h" for "ncstim.cc".)
The goldfish pigment sensitivity functions (pigm=16,17,18) are
from fundamentals defined in van Dijk and Spekreijse, 1984,
fitted to equations from Govardovskii et al. (2000).
See "goldfish.n" which was used to make "goldfish.h",
which contains the log(sensitivity) tables included in "wave.cc".
Then wave.cc generates log(specific OD) functions
in "wave.h" for "ncstim.cc".)
The 19,20,21 pigment functions are a cone from van Hateren & Snippe (2007)
and include the inner segment along with the outer segment. This model
includes adaptation and bleaching at high light levels
The 22,33 pigment functions are mouse cones from Lyubarski et al (1999).
The 24 pigment function is a mouse rod from Invergo et al (2014)
that includes adaptation. It runs slow because it uses 96 differential
equations.
The 25 pigment function is a human S cone with peak from
Dartnall, Bowmaker, Mollon (1983)
The "simple" pigment has no sensitivity function and little
transduction apparatus. Its conductance is modulated by a simple
saturation function:
The light absorbed by a photoreceptor is calculated from:
Note that the L <node> expression plots the amount of light
absorbed by a photorreceptor, i.e. it includes the effect of the
attenuation factors "attf", "dqeff", and the photoreceptor
sensitivity function.
Click here to return to Photoreceptor statement index
The "gain" parameter sets the gain of the amplifier, by default=1.
The "offset" parameter (default=0) is a voltage that is subtracted
from the voltage at node 1 and multiplied by the gain.
The "tau" parameter is the low-pass cutoff frequency.
The "delay" parameter allows a "vbuf" to function as an axon of
a neuron to carry an action potential from one node to another
node instead of requiring a set of compartments normally
generated by a cable. This scheme greatly reduces computation.
The voltages are passed through a "circular buffer"
that holds the data. The storage requirements are 10 floating-point
values for each msec of delay.
Click here to return to NeuronC Statements
The "maxcond" and "density" parameters define the open
conductance of the channels. If you need to create a channel of
a specific conductance at a node, specify the conductance with
the "maxcond" parameter. Otherwise, use the "density" or
"ndensity" parameters to specify a conductance density. The
"ndensity" parameter along with a unitary conductance (either
specified or default) defines the maximum conductance (see "see
setting unitary conductance and N" below. You should not use both
"maxcond" and "density" in the same statement, because they both
define the channel conductance.
If you define a maxcond of zero, the channel won't be created,
except if the parameter "nozerochan" is set to zero (default=1).
Click here to return to Channel statement index
If you prefer your "offset" parameters to
define absolute voltages instead of relative offsets, set
the default offset values in the beginning of your script
to the voltage thresholds you determine for your default
condition.
Click here to return to Channel statement index
If you prefer an "absolute" calibration for tau,
just set the value for "base tau" in the beginning of
your script to the time constant you determine for your
default condition. Then you can then specify the "tau" as
an actual time constant.
A longer tau than the default value causes the action potential
to be lengthened in time. A shorter tau shortens the action
potential. If both "taum" and "tauh" are changed by the same
factor, the action potential will retain the same general shape.
If they are not changed by the same factor, the action potential
shape will change and may fail entirely. If the time constants
are too short, the action potential will fail because capacitive
membrane charging shunts the ion currents and prevents voltage
from changing quickly.
Click here to return to Channel statement index
In their classic study of channel kinetics, Hodgkin and Huxley
(1952) used a temperature of 6.3 degrees Celsius. Since many
recent studies of channel kinetics have been done at 22 degrees,
this is the standard temperature for defining their rate
functions and unitary conductance. To simplify the kinetic and
conductance parameters, the Hodgkin-Huxley kinetic functions are
normalized to 22 deg C. For channels whose rate functions have
been studied at some other temperature, that temperature can be
entered as the standard temperature for the channel, or the
channel's kinetics can be normalized for 22 deg C by assuming a
temperature sensitivity (Q10) for its kinetics and unitary
conductance. For synaptic conductances the base temperature is
22 degrees C.
You can change the default base temperature for channel kinetics
(and unitary conductances) with the following variables:
The Hodgkin-Huxley type channels are normalized by multiplying
their rate functions by a constant factor ("dratehhx") that
increases their rate from the original (defined at 6.3 deg.
Celsius) to the correct rate for the base temperature (dbasetc =
22 deg C). This factor is computed by default from the standard
default "dqm, dqh, dqna, dqnb" values. However, it is not
affected if you change the value of "dqm, dqh, dqna, dqnb".
Instead, you can change it by setting the "dbasehhx" rate
multiplier variables:
The Q10s for Rm and Ri are active when the default values (drm,
dri) are used. When you set a "local Rm" or "local Ri" in a cable
or sphere statement its value is used unchanged. The default
values for "dqri" and "dqrm" are set to 1, and their base
temperature is "dbasetc", as above for channels. To activate
temperature compensation for these conductances, set the value of
"dqri" and/or "dqrm" to 1.3.
Click here to return to Channel statement index
If "unit" and "N" are both set and "maxcond" is not, the
conductance is set by the product of N times unit:
You can use the "ndensity" parameter instead of the "N" parameter
to define the conductance and noise properties automatically:
Click here to return to Channel statement index
Click here to return to Channel statement index
Na (green) and Kdr (red) channels voltage clamped in steps from
-70 to +20 mV. Note that Na currents are inward, activate
quickly, and inactivate after 1-2 msec, whereas Kdr currents
activate slowly and do not inactivate.
Click here to return to Channel statement index
Other discrete-state channels (type 1 and above) are
macroscopic descriptions of sets of channels in a membrane. The
population of a state represents its "concentration" as a
fraction of 1. The concentration of all states always sums to 1.
Each state also has a fractional conductance which when
multiplied by the effective maximum conductance "maxcond"
produces the instantaneous channel conductance. Microscopic
descriptions of channels are possible for the same transition
state diagram using noise parameters (see below).
When noise is added to these discrete-state channel types
(with the "chnoise" parameter), the population of a state is an
integer that represents the actual number of channels in the
state, and the number of channels that move between between
different states is an integer number calculated from the
binomial function. The total number of channels (i.e. from all
the states) remains constant. This scheme gives a very accurate
representation of the channel kinetics and noise. A time step of
50 usec or less must be used when discrete state channels are
given noise properties or the numerical integration becomes
unstable.
Top, eight-state Markov state diagram for Na type 1 channel. Time
courses of 6 of the 8 states are illustrated below. Middle,
average state populations for a typical action potential. Each
state varies between 0 and 1, and the total of all states is 1.
Bottom, same plot except noise for 100 channels added.
Transition between states is computed from binomial distribution
based on population of the source state and the probability of
the transition (rate function).
The function of the KA current in some neurons is to stablize the
membrane in combination with Na and Kdr channels. Since KA
activates and inactivates rapidly it is active during the time
when Kdr channels are building up activation, but during a
prolonged stimulus KA inactivates when Kdr is fully active. This
action tends to dampen oscillatory behavior. In a spike
generator, KA helps to terminate the spike, and is quickly
inactivated on hyperpolarization. In some neurons, it activates
at a more hyperpolarized voltage than Na channels, so it slows
down repolarization in the interspike interval.
Activation of K type 2 and 3 channels by a voltage clamp from
-70 mV to -10 mV. Dark blue traces show conductance. On top,
green trace is the "m" state variable (activation), and the light
blue trace is the "h" state variable (inactivation). At bottom,
each trace represents the fractional population of one of the
8 states.
Reasonable values of d1 and d2 are between .5 and 5. To eliminate
voltage sensitivity, set both d1 and d2 to 0 (which is default
for KCa types 0 and 1). A good start for the k1 and k2 values is the
average range of internal [Ca] expected. Above this average Ca
level, alphakca increases, and below the average betakca
increases.
Some KCa channels have minimal voltage sensitivity (SK type),
a small unitary conductance (~20 pS), and are thought to be
involved in lengthening the interspike interval. Other types
involved in spike termination have a large unitary conductance,
and both voltage and calcium sensitivity (BK type). If you
specify KCa type 0 or 1 channels (SK type) they will have no
voltage sensitivity by default. If you specify KCa type 2 or 3
channels (BK type) they will have voltage and calcium sensitivity
by default. You can change this default behavior by setting d1,
d2, k1, and k2.
The KCa type 2, 3 channels are similar to the 0, 1 channels
except that they are the "BK" type (sensitive to voltage and Ca,
with large conductance = 200 pS). They have different default
values for the unitary conductance and the d1, d2, k1, k2
constants.
The KCa type 4 channel is a sequential-state channel with 6
states that has no voltage sensitivity and is the best model so
far for the SKCa channel (apamin-sensitive). This channel is
derived from Hirshberg et al, 1998 (see chankca.cc for details).
As in the other sequential state channels, when noise is added
the states become populated with an integer number of channels
with the changes in population computed from the binomial
function. You can modify the activation and inactivation rates
with the parameters "taua" (Ca binding), "taub" (Ca unbinding),
"tauc" (opening flicker rate), and "taud" (closing rate).
The KCa type 5 channel is a sequential-state channel with 6
states that describes an sKCa channel with no voltage sensitivity
but insensitive to apamin. This channel is derived from Sah and
Clements, 1999 (see chankca.cc for details). Its affinity for
Ca++ is relatively high, so Ca++ unbinds slowly, which accounts
for the slow deactivation of the channel. You can change the Ca++
binding rate with "taua", the unbinding rate with the parameter
"taub", and the open/close flicker rate with "taud". You can test
these channels with the "tcomp/chantestkca.n" script.
The KCa type 6 channel is a sequential-state channel with 10
states that describes a bKCa channel with voltage- and
calcium-dependent gating. It is taken from Cox et al, 1997 (see
chankca.cc for details) in which a cloned "mslo" channel is
analyzed and an allosteric Markov model developed. The model
starts opening at ~100 nM [Ca]i but at a relatively high voltage
( > +30 mV), and at higher [Ca] it opens at more hyperpolarized
voltages.
You can change the Ca++ binding rate with "taua", the unbinding
rate with the parameter "taub", and the rates for the voltage
gating functions with "tauc" and "taud". You can change the range
of voltage gating with the d1 and d2 constants (as in the other
KCa channel types). You can test this channel with the
"tcomp/chantestkca2.n" script.
The Cox et al. Markov model is valid for a wide physiological
range of [Ca]i and voltage, but is recognized to be incorrect for
zero [Ca]i or for extremes of voltage. In this MWC-type model, 4
subunits have independent binding of Ca++, can remain closed
during Ca binding, and the channel has a concerted voltage-gated
opening. The effect of [Ca] on opening is to shift the channel to
liganded states which have different forward and reverse rate
functions for voltage gating, effectively changing the voltage
range of gating, though the gating function is unchanged. Gating
of the BK channel is among the most complex known, since the
channel has numerous open and closed states and can open almost
fully in the absence of [Ca]. More recent studies have ruled out
this MWC-type model, and we are awaiting a better Markov model
for the BK channel.
The ClCa type 2 channel is identical to the ClCa type 1 channel except that it
senses [Ca]i in any shell or the Ca core, set by the parameter "dsclcac"
(default=10). Its voltage sensitivity is controlled by "dclcavsc" (default=2.0)
which multiplies the forward rate of binding by [Ca]i at the shell described
by "dsclcac" over the range of 120 mv, starting at -40 mV.
Currents through a K type 4 channel (Ih current). The cell is
clamped to -30 mV and then stepped to -50 down to -110 mV for 500
msec, then stepped to +30 mV. Note that the activation currents
have a long time constant but deactivation is short, and that
the channel does not inactivate.
The K type 4 channel is a sequential-state version of the
Ih channel from photoreceptors. It is activated when the
membrane voltage hyperpolarizes beyond -50 mV, and has a
slow activation time constant, between 50 and 200 msec. It
does not inactivate, but deactivates at voltages more
depolarized than -30 mV with a time constant between 20 and 50
msec. Normally K channels have a default reversal potential set
by the K Nernst potential to near -80 mV, however for the Ih
channel the default is -20 mV. You can change the reversal
potential with the "vrev=" option.
Click here to return to Channel statement index
Since the channel imitates a Na channel it can only
depolarize so another channel (typically a K channel) is
required to set up a working spike generator. This channel
can therefore be used in combination with other channel
types to test out hypotheses in a way not possible with
standard integrate-and-fire spike generators (because they
don't work with a standard compartment that sums the
synaptic inputs and the spike currents).
To look inside the operation of the IF NA channel, you can
plot the G1 and G2 values to show the population of the two
states; G2 is the conducting state. Plot G3 and G4 to look
at the integration and state switching.
Click here to return to Channel statement index
The calcium compartment contains a series of concentric shells of
"cytoplasm", each the same thickness, that restrict the flow
of calcium into the interior of the cell according to the law of
diffusion. The parameter "cshell" sets the number of shells
(default 10). The parameter "dcashd" sets the shell thickness
(default 0.1 um). The inner part of the cell is considered to be a
well-stirred "core" with a uniform concentration of calcium. In
a dendrite that's too small to fit the number of shells, the
thickness of the shells is reduced so they fit. Only the calcium
concentration at the outer shell "Ca(1)", next to the membrane,
affects the membrane reversal potential. The parameters "cao" and
"cai" define the starting concentrations of calcium in extra- and
intra-cellular space, respectively. The parameter "caoshell" sets
the number of shells in extracellar space (default 1). The
parameter "ddiacao" sets the effective diameter of the
extracellular "core" for calcium diffusion. The parameter "ddcao"
sets the diffusion constant for extracellular calcium. The
parameter "dcasarea" sets the effective area of the shells for
calculating the Ca flux (default set by morphology). The
parameter "tcai" specifies the threshold below which internal
calcium is not pumped. The parameter "cadia" multiplies the
diameter automatically set for a calcium compartment created in a
cable. You may also specify a calcium compartment with the "at
At each time step, the calcium flux through the membrane
is computed from the sum of the current through the calcium
channel, the calcium pump, and the sodium-calcium exchanger.
This flux is then added to the compartment and calcium
diffusion between the concentric shells is computed.
Click here to return to Channel statement index
Dynamic calcium buffering in the shells is specified with
the "cabuf" parameter. The total concentration of buffer is
set by the "btot" parameter ("btoti" for the first shell).
Calcium binds to the buffer at a high rate that is
proportional to the concentration of both calcium and
buffer:
The forward rate is dependent on the concentration of calcium and
buffer. The reverse rate is a function of time and is
independent of concentration. If the forward rate is not set
(with "vmax"), the default values are dependent on temperature
(Q10 set by "dqcab", default=2).
Note that when the "cabuf" parameter is defined, the "cbound"
parameter is ignored.
Click here to return to Channel statement index
Its current is:
Note that the pump current is independent of membrane voltage but
is dependent on the internal Ca concentration. If the pump
"vmax" is not set, its default value is "dcavmax". It is
dependent on temperature (set by its Q10 value, "dqcavmax"
default=2).
For a simple model, you can set up exponential decay for [Ca]i
by setting just one shell, and eliminating diffusion to the
internal core. For this purpose, set the Ca pump Km a little
higher than the expected maximum [Ca]i (so the pump rate is
proportional to [Ca]), like this:
Note that the exchanger current is dependent on membrane voltage
and on the concentration of both internal and external Ca and Na
and temperature. At low internal Ca concentrations the exchanger
supplies Ca to the cell which raises internal Ca and generates a net
outward current. At high internal Ca concentrations the exchanger
extrudes Ca from the cell which lowers internal Ca and generates
a net inward current.
For simulations with typical concentrations and temperatures
(temp = 22-35 deg C, dcao = 1.15 mM, dnao = 143 mM, dnai = 12.5
mM, i.e. Ena = +65 mV), the equilibrium point ranges from 90 to
150 nM, so typically the exchanger tends to deplolarize. The
pump and exchanger rates therefore can be adjusted to achieve a
balance at one concentration:
This behavior is controlled by several parameters:
When you specify the "cakd" parameter, calcium binds to the
channel and causes it to close. It uses the following equation:
However, the Nernst potentials "vna", "vk", "vcl", etc. are not
equal to the reversal potential that is experienced by a channel,
for several reasons. Other ions besides the channel's major ion
can pass through the channel and this affects the reversal
potential, defined by the "GHK voltage equation" (see "Reversal
potentials, Nernst and GHK equation" in the first section of the
manual). Also, when the internal and external concentrations of
an ion such as Ca are very different, the effective driving force
for the channel changes with membrane voltage (see "Current
through Ca channels" above).
The reversal potential for a NeuronC channel is set by default
to its GHK voltage, calculated from the concentrations of
various ions and their permeabilities through the channel. The
internal and external concentrations for an ion are set by
default from predefined Nernst potentials for the ion (i.e.
vna, vk, vcl), but you can change these values to give
arbitrary Nernst and reversal potentials.
Note that the default reversal potential for a channel and
the Nernst potential for an ion are functions of "tempcel" =
temperature (see "Reversal potentials, Nernst and GHK equation"
in the first section of the manual). They are also functions of
the "surface potential" that is created when external calcium
concentration is high (see "Voltage offset from external calcium"
below).
If you want to ignore the GHK voltage equation and set reversal
potentials from the Nernst voltages vna, vk, and vcl, you can
set the relative permeabilities of channels to their minor ions
to zero:
If you specify the internal Ca level (cai) this will override the
default internal concentration at the Ca compartment associated
with the channel, and the Ca channel's current and reversal
potential will be modified accordingly from the GHK current and
voltage equations assuming a default level of K permeability
(dpkca = 0.001 by default). If you set the Ca channel's reversal
potential (vrev) this will set the internal calcium for the
compartment also assuming a default level of K permeability.
If you specify both internal calcium and reversal potential (cai
and vrev) the calcium flux will be set by the levels of cao and
cai, and the Ca channel's total current will be set by vrev,
assuming for both the GHK current equation but not K
permeability. This would be the case, for example, if you don't
want to use relative K permeability in Ca channels (dpkca) but
want to define the reversal potential and the resulting total
current through a Ca channel.
If you set:
Setting the right internal and external ion concentrations is a
bit tricky, and has been designed to be automatic so no changes
are necessary for most simulations.
Here's the sequence: the vna, vk, and vcl values are set
arbitrarily to +65, -98, and -70 mV. Then the external ion
concentrations are specified (from Ames & Nesbett, 1981, i.e.
the composition of Ames medium, and Hille, 2nd ed and some
retinal papers: dnao=143, dko=3.6, dclo=125.4 mM). Then using
the vna, vk, and vcl values and the external concentrations, the
internal concentrations are set from the Nernst equation at 37
degrees C. These are the default values.
If the user wants to set the Nernst potentials vna, vk, or vcl,
these values could then be used to recompute the internal ion
concentrations from the Nernst equation at whatever temperature
is currently set. One problem with this method of setting the
internal ion concentrations is that internal K+ concentration
varies a lot when temperature ("tempcel") is changed. This is not
really correct, as a typical cell regulates its membrane
potential and ion concentrations quite tightly. However it is not
known exactly which parameters in the real physiology of a cell
have priority over others when external ion concentrations or
temperature change.
One would like a method for simulating control of ion
concentrations and reversal potentials that mimics various types
of physiological dependence of Nernst potential and internal ion
concentrations on temperature. This strategy is implemented in
NeuronC with the variable "calcnernst" which sets the simulator's
priority for ion concentrations and Nernst potentials. If
calcnernst = 0 (the default), the internal ion concentrations are
recomputed from the temperature and the Nernst potentials.
However, when calcnernst = 1, Nernst potentials are recomputed
from temperature and ion concentrations.
If "calcnernst" is set between 0 and 1, (default 0.6) a hybrid
strategy is used where Nernst potentials and ion concentrations
both change. A new reversal potential is calculated from the
temperature and ion concentrations, but "calcnernst" sets the
"fraction" of this value that is used. The difference is made
up by a change in internal ion concentration. For example, if
calcnernst=0.9, most of the change is assigned to the Nernst
potential, and the ion concentrations change only a little.
Note that for this strategy to be useful, you should not change
both Nernst potentials (vna, vk, vcl) and ion concentrations
(dnai, dki, dko), since these parameters are automatically set at
run time. If you want to precisely define the Nernst potentials
at different temperatures, then you can set "calcnernst=0" and
the ion concentrations will be recomputed. Otherwise, if you want
to keep ion concentrations precisely defined, you can set
calcnernst=1, and the Nernst potentials will be recomputed.
Of course at any time "vrev" for a synapse or channel can be
defined which overides the Nernst potential and the channel's
default value.
These additions have the effect of making the simulator more
realistic, but there is a *price* for it. The default reversal
potentials for the channels are not vna, vk, or vcl. They are
calculated from the GHK voltage equation so they represent all
the ion currents that flow through a channel. The currents are
defined by setting permeabilities for several ions for each
channel.
What this means in practice is that vrev for an Na channel is
*near* +40 mv (43 at 22 deg and 47 at 37 deg), and *near* -80 for
a K channel (83 at 22 deg, and 82 at 37 deg). So the reversal
potentials are close but not exact to the usual values, and they
change with temperature and the ion concentrations and
permeabilities.
If you would prefer to have the Nernst potentials define the
reversal potentials for channels, you can set the permeability
for each channel type to be exclusively for the major ion, (i.e.
set dpnak, dpkna = 0). Then you can set the reversal potentials
for all the channels with vna, vk, and vcl.
The permeabilities are set to default values (dpkna, dpnak,
dpkca, etc.) in the channel definitions (in "chanxxx.cc"). However,
to change the value of the Ca permeability for a channel, you
can set its "caperm" parameter. This overrides the channel's
default Ca permeability. Note that caperm and the default
parameters range from 0 to 1.
When the internal and external ion concentrations are different,
the instantaneous current through an ion-selective channel is a
nonlinear function of the voltage. This is computed using the
GHK current equation. The "nc" simulator uses the GHK current
equation when the variable "use_ghki" is set to 1 (default 0).
The GHK current equation calculates the effective conductance
from the voltage and the internal and external ion concentrations.
The internal ion concentration is set for each channel type by
the Nernst equation, from the external ion concentration and the
reversal potential. The reversal potential is set by default for
each channel type but can be overridden in several ways.
One way to set the reversal potential for a channel is to set
its corresponding "ion reversal potential":
Channels such as AMPA and NMDA channels are non-selective and have
permeabilities to both Na+ and K+ ions. When the concentration
gradients for the 2 ions are equal and opposite, the channel acts
like a linear conductance, with current proportional to the
membrane potential.
When a channel has such a major permeability to 2 ions, their
permeabilities and concentrations are both taken into account
when computing the GHK equation. The permeabilities are computed
from the reversal potential and the original default
permeabilities using the GHK voltage equation in an iterative
procedure.
Another way to set the reversal potential for a channel is to
individually set the reversal potential "vrev" for each channel
when it is created. If this reversal potential is different than
the default value, the channel gets an individual copy of the
reversal potential. If you set "use_ghki=1", then the channel
also gets a new set of ion concentrations and permeabilities from
its default channel type definition. These are used the GHK
voltage equation to generate a new set of permeabilities and
internal concentrations specific to that channel. Then the
"slope conductance" and "slope reversal potential" are computed
as described above and lookup tables are created for that
individual channel. This is relatively fast at run time but
requires a lot more memory to store the lookup tables when many
individual channels are set. When the channel has only 1 major
permeability, the reversal potential is used to set the internal
concentration. When the channel has 2 major permeabilities (as
described above), they are revised and iteratively from the
concentrations which are not changed.
Click here to return to Channel statement index
To disable the automatic computation of voltage offset, set
"dcavoff=0" in the beginning of your script. This is not
normally necessary, however, as the voltage offset is zero if
"dcao" or "dcoo" is not changed. If you want to set the [Ca]o
for some channels without causing a voltage offset, set the "cao"
parameter for the channel without changing "dcao":
To turn off this feature, you can set either "dcavoff" or
"dcaspvrev" to zero, or you can leave "dcao" set to its default
value:
Trace of a K channel in a small patch of membrane (green) that
contains channel noise (large jumps) and Johnson noise (small
fluctuations) filtered at 1000 Hz, and an identical channel on a
separate patch of membrane (red) without Johnson noise. Channels
are voltage clamped to -20 mV. Note that the K current is
outward.
You can change the default base temperature for unitary
conductances (and channel kinetics) with the following variables:
See the description of "synaptic vesicle noise" above for a
discussion of the random "seed" and how to change it.
For all channel types:
If the channel is a Na type 4 (Integrate-and-Fire)
You can also define your own rate functions for existing channels
by writing the functions in a simulation script. These functions
are used instead of the default ones at the beginning and also
whenever the time increment changes during a run. For example,
you could change the sensitivity to voltage for activation (the
alpha rate function) and this would modify the range over which
the channel would start to activate.
The default transition rate functions in "nc" are exactly as
defined by Hodgkin and Huxley (1952), from the membrane voltage
in mV. A channel's default rate functions are defined in the
file containing the channel data structures (e.g. channa1.cc for
Na type 0 and 1 channels).
To replace these predefined functions, make your own functions
that define the alpha and beta rates, normally called "calcna0m"
(calculate m for Na type 0), "calcna0h", etc., in your script
file that you run with "nc". For the interpreted version,
whenever any of these functions are defined inside your file,
they are used automatically instead of the default ones. For
the compiled version, you must call set_chancalc() to replace the
default kinetic function for the channel before the channel is
defined or used. The functions return their respective rate
constants and have two parameters: a) membrane voltage, and b) a
number describing the function (e.g. 1 = alpha, 2 = beta, etc.).
Voltage is calibrated here in mV, using the modern definition of
"membrane voltage" (i.e. cell membrane voltages are negative when
hyperpolarized). This definition of voltage differs from the
original Hodgkin and Huxley (1952) paper but is more convenient.
The functions define rate per sec.
Example:
Click here to return to Channel statement index
Distributed macroscopic channels are available for cable
membranes and are defined much like the "chan" statement,
except that their maximum conductance is defined as a function
of the membrane area and not as an absolute conductance.
Multiple types of channels may be defined by including multiple
channel options in sequence after the "cable" statement. See
"cable".
Click here to return to Channel statement index
Each channel is checked against every other one in the
compartment to see if they are identical in their properties
(vrev, voltage offset, tau, unitary conductance). If they are,
their conductances and values of "N" (number of unitary
conductances) are added together. The value of N is a floating
point number so if the channel conductance is low, the fractional
channels from several compartments can add to give a final value
of N greater than 1 (or higher integer). After this process, the
value of N is rounded up to the nearest integer so the channel
stochastic noise computations can be correctly run with the
binomial distribution (see "Markov noise") below.
To see this process work, you can set the "lamcrit" variable or
the "-l" command-line option: a lamcrit value of 0 prevents
condensation of any kind so you get lots of compartments.
Setting lamcrit to .001 prevents compartment condensation but
activates channel condensation, and a value of lamcrit in the
range 0.1-1 will give both compartment and channel
condensation. Use the "nc -p 1" option to print out the
compartments and channels.
Click here to return to Channel statement index
You can set up a channel to sense the external
compartment using the function "addchan_extern()". For calcium
channels, you use the function "addchan_extern_ca()
Note that every node contains a pointer to the compartment
that represents the node. The compartments are created after
a "step()" statement.
You can set up capacitive coupling through the membrane with
the function "addcomp_extern(extern_comp, intern_comp):
Most of the stimuli provided in nc come in several different versions. A version
with many parameters gives flexibility, and the versions with fewer parameters
set some of the parameters with default values. See "ncstimfuncs.cc" for definitions
of stimulus procedures.
For the sine wave grating (sine, gabor, sineann, windmill) stimuli, two
intensities can be specified (see ncstimfuncs.cc). The "inten_mult" intensity
is multiplied with the sine wave and serves as a scaling factor for contrast.
The "inten_add" intensity is added to the resulting sine wave to provide a
local mean intensity. Both the sine wave and the mean intensity are added to
any other stimuli including the background set with "stim_backgr()". The
"makenv" parameter controls the outer edge of the stimulus. If it
is set to 1, the edge will have a gaussian decay with radius, but if it
is set to 0, the edge will decline to 0 immediately with radius.
The "stim spot", "stim bar", "stim sine", "stim gabor",
"stim windmill", and "stim sineann" statements allow large fields of
photoreceptors to be given an optical stimulus. These statements
are interpreted at run time by "nc" so that the photoreceptor
receives the appropriate amount of photon flux. Stimuli are
additive so multiple simultaneous stimuli may be given without
interaction. "nc" does no blurring at run time.
Note that "nc" can generate all the stimuli correctly except for
blur and scatter. The idea is to run the "stim" program once to
generate the stimulus file. When you then run "nc", it will use
the stim file to generate the optical stimuli instead of
generating the stimulus again each time you run the simulation.
Because the stim file defines the light flux for each
photoreceptor, each time you change the stimulus or the
location of photoreceptors you'll need to run stim again.
You can also generate the stimulus file with "nc" by setting the
"makestim" parameter to 1, i.e. include "--makestim 1" on
the command line.
If you don't have optical blur or scatter, you can just run "nc".
But this can in some cases use a lot of memory to store
the photon fluxes for each photoreceptor. For example,
for a large cone array and a long duration drifting sine
wave grating, the stimuli can take many MB of memory.
Also, note that "nc" interprets all the non-optical stimuli,
i.e. "stim rod", "stim cone", "stim cclamp", "stim vclamp".
The stim file only contains optical stimuli.
To see how these functions were created, look in "linesp.c" and
"linespr.c". A point-spread (2D) scatter function is generated
and convolved with a line. The resulting line-spread function is
sampled and compared with the original data (which is usually in
line-spread form). If the original data is a MTF (modulation
transfer function), then the line-spread's Fourier transform must
be compared. The point-spread function's parameters are modified
until the comparison is satisfactory. The scatter functions
given above are within 1-2% of the original data but it is likely
that better approximations can be found.
If the original blur and scatter line-spread functions are
Gaussian, their radii can be used directly in the 2D point-spread
function and only the relative amplitude of the scatter function
must be determined by fitting. The reason is that a Gaussian
function is (x,y) separable, i.e. a section through a 2D Gaussian
(a Gaussian of rotation) looks Gaussian in 1-D. Other radial
functions not (x,y) separable can be readily fit using the method
described above. Robson & Enroth-Cugell (1987) derived the
pow(r,2.5) point-function analytically from the measured
pow(r,1.5) line spread function.
To run the convolution at finer resolution than 1 micron
in the stimulus position, set the "sscale" parameter which
magnifies the resolution of the convolution arrray (e.g.
sscale=.2 means magnify by 5 times). Of course, if you don't
require blur, you will not require the convolution and therefore
don't need to run the "stim" program or the stimulus file it
generates. In that case, full "floating-point" precision (6
decimal places) is available for the stimulus position.
The convolution that "stim" performs goes as follows: for
each photoreceptor, each element in the "blur" array is
multiplied by the corresponding element in the "stimulus"
array. The sum of these multiplications becomes the
stimulus intensity for the photoreceptor. In order to save
space, the "blur" array is made only large enough to hold
the Gaussian blur. The array is created with a radius of 5
times the standard deviation of the Gaussian blur specified
by the "stim" statement. If the "sscale" factor is defined
smaller than 1, the blur array is made larger.
To make the stimulus file, run "stim" on the simulation
program that contains the "stim file" statement. "stim" will
create the stimulus file automatically. Thereafter, "nc" may be
run on the same simulation program, reading its stimulus from
the stimulus file defined in the program. The "stim file"
contains one line for each change of light intensity for each
photorecptor. The "stim file" is a text file and you may view
and modify it with a text editor. It is written (by "stim") by
the subroutine "stimfmout()" in file "stimsub.c" and is read (by
"nc") by the subroutine "readstim()" in file "ncstim.c".
Large stim files may be compressed with "gzip" which will
add ".gz" onto the end of the file name. If the compressed
stim file exists and the original does not, "nc" will read
the .gz file and decompress it with the "zcat" command. The .gz
file size is typically 10% of the original text version. For
this scheme to work properly, both "gzip" and "zcat" must be
avalable in your shell PATH environment variable.
The spatial extent of the grating is defined by the "xenv" and
"yenv" parameters, which define the radii of the X and Y
dimension Gaussian envelopes for the "Gabor" function. For the
"sineann" funtion "xenv" gives the radius of the envelope. Note
that many complete sine-wave cycles may exist within the
envelope. If no xenv and yenv values are given for the "Gabor"
or "sineann" statements, they default to 50 um Gaussian radius.
For a "sine" grating, the envelope function is set by default to
infinity, and its extent from its center is set by "xenv" and
"yenv" (which for "sine" defaults to infinity). In every other
respect a "sine" grating is identical to a "Gabor" grating. The
"sineann" grating is a concentric sinewave grating, where the
extent from the center is given by "xenv". Outwards motion is
set by a positive value for "drift". The "windmill" function
is identical to the "sineann" function except that it generates
a sine windmill orthogonal to the "sineann" stimulus, and the
number after "windmill" is the number of windmill vanes.
This type of masking stimulus is useful when stimulating with a
moving grating, to prevent motion in part of the stimulus from
being seen. The mask intensities are additive like ordinary
stimuli, so a mask can be built up from any comination of
spots or bars.
To generate a mask complementary to a stimulus pattern, set the
variable "unmaskthr" to a negative value (e.g. -100), and set
your masking stimulus to a more negative value (e.g. -200). When
the stimulus is processed, any masking values more negative than
"unmaskthr" become unmasked. This allows you to generate a mask
with a hole in it:
The "backgr" stimulus statement is required to generate the mask
surrounding the spot since the spot (mask) statement only generates a
mask intensity inside the spot.
However, to set a photoreceptor (rod, cone, or transducer) to be
sensitive to only one stimulus channel, you can set the stimchan
parameter for the photoreceptor. If the stimchan parameter is set
to zero (the default), the photoreceptor will be sensitive to all
the stimulus channels, but if it is set to a value from 1 to 9,
it will ignore any other stimulus channels. This allows you to
create different stimuli and blur for different neurons.
Note that setting the stimchan=0 for a stimulus does not stimulate all
the stimulus channels -- this only works for photoreceptors, i.e.
setting stimchan=0 for a photoreceptor causes it to receive all
stimulus channels. Also note that you must set the stimchan appropriately
for the background intensity, as well as for the stimulus intensity.
The stimulus on and off times are rounded up using a time step defined by
"srtimestep" (default = 0.0001 sec) which can lead to inaccuracy in the start
and stop times of stimuli of 0.1 msec. The reason for rounding up the stimulus
times is that the simulation time "simtime" is advanced as a continuing sum of
small timesteps which has inherent roundoff error -- and the stimulus on and
off times are directly compared with this continuing sum, which can cause
stimuli to be missed.
For most models, the rounding of stimulus on and off times is is not a problem,
but if you need very accurate on and off times, you can set "srtimestep = 1e-6"
which will make the stimulus on and off times accurate to 1 usec. The
disadvantage of using this smaller roundoff value is that for long simulations with a
short time step, roundoff error builds up, causing on and off times of stimuli
occasionally to be missed -- which is a serious problem for a model.
If you want to set "srtimestep = 1e-6" you should keep the number of total time
steps for the simulation (i.e. endexp / timinc) less than 1e7, which will maintain
10 digits of precision in "simtime" and prevent stimuli from being missed.
The printout of the "plot" statement represents the value of
stimulus and record parameters at the beginning of the time
step, before the simulator integrates to the end of the
timestep and computes the voltage values. This means that after
a "step" statement, the last plotted values are not always the
most recent ones available. Normally this is OK because in a
series of "step" statements the next "step" allows the "plot"
statement to print out the next set of values. If you want the
last plot statement to correctly reflect the ending values, set
the "endexp" variable to the ending time of the simulation.
When the simulation time equals the value of "endexp", the
"plot" statement adds one last printout of the values of
stimulus and record parameters that are valid at the end of the
last time step. To change the maximum and minimum values for
the X axis, set the "setxmax" and "setxmin" parameters.
The plot statment has several forms. If the voltage at
several nodes needs to be plotted at the same scale, a
combined plot statement may be used:
Several "plot V[]" statements may be used to cause
several plots to be displayed on one graph, but with
different scales. The first one defined determines the
scale actually plotted on the vertical axis, but the rest
simply use their own scale and ignore the scale numbers on
the graph.
The "filt" option inserts a lowpass filter in the plot to
reduce the bandwidth of the recorded signal. The value given
sets the time constant of the filter in seconds [1/(2*PI*F)]. You
can also set a cascade of filters:
(interpreted:)
To make a Bessel filter, use this statement:
You can also load an array with plot values using the "plarr
The FA0-FA4 values are pre-release time functions, calibrated
in "volts above synaptic threshold". FA8 gives the "readily
releasible pool", and FA9 gives the instantaneous
"trel" (transmitter released) vesicle release rate in
vesicles/sec. The FB0-FB4 values are post-release functions and
represent the concentration of neurotransmitter in the synaptic
cleft. FB0-4 range from 0 to 1000, where a value of 1 represents
the half-saturation point for the static post-synaptic saturation
function. The FC0-FC4 values are post-saturation conductances.
FC9 is the second-messenger level. They return a value
normalized to the range 0 - 1. This value is multiplied by the
"maxcond" parameter to set the post- synaptic conductance. The
values FA0, FB0 and FC0 return the input to their respective
filter functions.
Using the "G", "G(1)-G(12)" expressions, the channel
internal states may be recorded (see "plot" below). The
expression "G(0) <expr> records the channel conductance in a
manner similar to the "FCx" expression (calib. in S). For a
"sequential-state" type of channel (type 1), the "G(x)" (x=1-12)
expression records the channel state concentrations,
(dimensionless fractions of 1). Each of these plot
expressions has a default max and min to set the graph
scale (e.g 2, 0 for states, 100e-6 for nt, etc.)
For all channel types:
If the channel is a Na type 4 (Integrate-and-Fire)
The synaptic filters return values between 0 and 1
representing the amount of neurotransmitter released (see
"plot" above). The "FAx", "FBx", and "FCx" synaptic filter
functions require an element number which has been set
through the "ename" clause in the original definition of the
synapse.
The value G0 returns the total channel conductance, and
the values G1-G8 return the concentrations of the states 1-8
respectively, or in the case of Hodgkin-Huxley type
channels, G1,G2 return "m","h" for the Na channel, and G1
returns "n" for the K channel.
The graph statement is useful for displaying parametric
equations like I/V plots, where both are functions of time. In
this case, the "step" statement can be used to set up a short
simulation which can be continued to gather further graph
points:
Example:
You can set the display to make separate plots for each
trace with the "plsep" parameter. If you set "plsep=1"
then the screen will be divided into separate plots, each with
its own y axis and label, and with a common x axis, so that all the
traces can be more easily distinguished. By default, "plsep"=0"
so if you want separate plots you will need to set it to 1.
You can set "plsep=1" in the script, or from the command line,
like this:
If you are using "plsep" mode for separate plots, you can assign
more than one trace to a plot with the "plnum x" parameter. Each
trace can be assigned to a "logical plot", and more than one
trace can be assigned to a logical plot. The logical plots are
then assigned to the display in increasing order. For example:
In this example there are 3 plots, which are logical plots 2,
10 and 11. They are displayed on the screen starting from the
bottom as 1, 2, 3. Each trace can be assigned pen color, but if
no pen color is given, its color is assigned from the plot
number. A label for V[3] (the second trace in "logical plot" 2 )
could be displayed, but in this case its "plname" is not given so
a label is omitted for this trace. If the first trace is not
given a "plname", all the traces in the plot are labeled
according to their node or element numbers or their "plname".
With suitable "max" and "min" parameters, the traces in logical
plot 2 can be offset so they overlap a desired amount. Any plot
statements without a logical plot assignment are assigned
independent plots.
You can also change the size of the separate plots, to make their
Y axes bigger or smaller. Use the "plsize x" parameter. The
first trace sets the size. All the sizes are scaled to fit
inside the window.
To simplify placing traces within a plot, you can set the
"max" and "min" parameters e.g. like this:
In this case, the "plg" variable is the "plot gain", "offtr" is
the offset for the trace within the plot (range of 0 to 1 is size
of plot), and "offb" is the zero offset in the units for "plg".
To make the trace larger, increase "plg", and to shift it up or
down, change "offtr" or "offb".
Example:
The selected neural elements appear on the screen with
the view selected by appropriate rotation and "center"
commands. Each neural element is displayed with a simple
icon in a position corresponding to its location in the
circuit. In order for neural elements to be displayed in
their proper place, the location of each node must be
defined with the "loc (x,y)" clause when a node is set up
with a statement beginning with "at" or "conn". (If this is
not done, the location of a node is 0,0,0). Note that rods
and cones also have a location for their transduction
element, which is not necessarily the same as their node's
location. For example, to set up a cable connected to a
sphere, you could say:
The addition of "only" to the ""display matching <node>
statement displays only those neural elements "at" the
"<node> given, or those elements that connect exclusively
with that "<node> Given the circuit in the example above:
The "display connect <node> to <node> statement
displays all the neural elements that match and connect to
both "<node> values. For instance, in the example above,
the statement:
The "display range
The display element <expr> statement displays one neural
element that has been remembered with the "element <expr>
statement. This is useful for displaying one specific
element of several that connect to identical nodes.
Click here to return to Display statement index
The "dscale" parameter causes the icon of a neural element to
be displayed in a different size than normal, without changing
the size of the element. It is sometimes helpful to display the
icon larger to make it more visible, or smaller to allow more
space between icons in an array.
When displaying nodes (-d 8), the dscale parameter can also
select which node number dimension (1-4) is displayed, along with the size.
A negative number selects this option. When dscale is negative,
the sign is ignored, and the integer part selects the node number
dimension, and the fractional part to the right of the decimal point
selects the size.
The "rmove (x,y,z)" parameters cause the objects selected to be
displaced (translated) during display. This is useful for
"pulling apart" a neural circuit into its separate neurons. The
move only takes effect for objects displayed within the same statement.
You can display the voltage of a neuron by displaying it with a
color of "vcolor". The range of colors is distributed between the
range of the "max, min" parameters. The colors range from the
cool colors for "min" to the warm for "max". The amount of light
received by photoreceptors can be displayed with "color=lcolor",
and display of [Ca]i by "color=cacolor". To display different
colors for each region, set "color=rcolor".
To display the stimulus during the simulation, you display the
light that the photoreceptors currently sense at this instant,
using (no "at" clause):
Note that if a "step" or "run" statement comes before a "disp
stim" statement, the "disp stim" statement will always show
the stimulus at the current simulation time, even if an "at"
clause is included.
The display stim" statement displays the light value as the color
of a small sphere (default 1 um diameter). Often one wants to
display photoreceptors a little larger than the default size with
the "dscale" parameter:
Each type of "display" has its own default colormap, but you can
set another colormap with the "cmap = <expr>" parameter.
The "display stim" statement defaults to a grayscale colormap but
you can set it to a colormap with colors using "cmap = 3":
You can define your own colormap by creating a one-dimensional array
and placing sequential color values into it. Note that the color values
are the unique colors are already defined in the various drivers
(i.e. color "32" is grayvalue 0 from colormap 3, "195" is grayval99).
For more details on the "bigger variety" colormap 8, see
"nc/pl/ccols.txt" (taken from "/usr/lib/X11/rgb.txt"). You can
see these colors and their names with the program "xcolorsel".
To add or modify these colors, see "nc/src/ncdisp.cc",
"nc/src/colors.h" and "nc/pl/mprint{x,c,xf}.c"
A display statement runs in "construction" mode. To see the
progress of the construction of a neural circuit, a stimulus, or
the color display of voltage or calcium, you can place "display"
statements between "step" statements:
To make a movie of the spatiotemporal propagation of voltage or
calcium concentration in a neuron or in a network, you can place
"display" statements inside the "onplot" procedure. This is a
special procedure that runs at intervals during the simulation,
just after any "plot" statements generate their output:
You can add a color definition bar like this:
In the example below, the _COL rows in the density file have different actions:
make_movie3d:
make_movie_stim:
Then run this command:
Click here to return to Display statement index
Click here to return to Display statement index
Within the draw procedure, you can use or ignore any of the parameters.
The "pigm" and "dia" parameters are the numbers you set (or were
set by default) for the photoreceptor definition. The "type" is
"rod" or "cone". The "color"
parameter is defined by the following search: if your "display"
statement defines a color, then this is used, otherwise a standard
color representing the pigment type is used. The "dscale"
parameter is a copy of the "dscale" parameter in the "display"
statement. It allows you to change the size of an object for
display purposes only without changing its actual size.
Generally you want to multiply the size by dscale inside your
procedure, but other uses are possible, for example, you could
have integer values (or negative values) of "dscale" select for a
different of icons. The "dist" parameter represents the amount
of foreshortening of the object's icon by the rotation it
undergoes (see below). The "hide" parameter is set to 1 whenever
"hide" is set, in which case the icon should be a closed unfilled
outline, i.e. a polygon.
Just before your procedure is called, the "graphics pen" is
moved to the (x,y,z) location of the photoreceptor and a graphics
sub-frame is initiated that is rotated with respect to the root
frame. If the icon is oriented (e.g. extended vertically like a
photoreceptor), you draw it horizontally to the right (i.e.
horizontal is "zero" degrees rotation). The icon may be
foreshortened by some 3D rotations, so to correctly take this
foreshortening into account, multiply its length by the
"forshortening" parameter. This parameter varies from 0 to 1. If
you ignore the foreshortening, your icon will be displayed the
same size no matter what rotation.
You can use any graphics commands to draw the icon. The graphics
scale is in microns but this can be changed with "gsize()".
If you want to draw something on top of a display of a neural
circuit, you can use the "transf()" subroutine to give the
rotated 2D coordinates of a 3D point:
You can use the "xt,yt" values passed into the "gmove()" and "gdraw()"
functions to draw. The "zt" value can be used to decide whether
one object is in front of another.
Note that a channel specified as a density cannot be named in
the same way because a density statement defines channels
in multiple compartments.
A typical use for the ename of a channel is to retrieve the
fraction of inactivation of Na+ channels at a node:
This example constructs a presynaptic terminal that
connects to a postsynaptic cell with a synapse. The synapse
releases neurotransmitter exponentially with voltage,
calculated at the standard time resolution of 0.1 msec.
However, every "synstep" (10 msec) time interval, the
synapse's conductance is modified according to the function
"modsyn" which can be any computable or recordable function
(e.g. it may be a function of voltage or conductance at any
node in the network). The pre- and post-synaptic nodes
are given as parameters to the function. Then the
simulation continues to run with the "step" statement, which
is similar to the "run" statement except that it stops the
simulation after the given time interval:
The "erase model" statement erases all arrays
and neural circuits, so a simulation can be
started over within one session of running "nc".
Whenever "nc" runs, of course, everything is
already erased, thus normally there's no reason to
"erase model".
The "erase array" statement erases a dynamically-allocated
array.
The "erase node" statement erases a node and any elements that
connect to it.
The "erase element" statement erases an element and any nodes
that connect to it.
Note that you can erase elements or nodes within a foreach
statement but in this case you may only erase the node or element
provided by that iteration of the foreach. If you try to
erase any other nodes or elements, undefined behavior may result.
The reason for this restriction is that the foreach statement
cannot find the next node or element if you erase it.
See example in description of "foreach" below).
The "save model" and "restore model" statements allow you to
run a model, save its state, and later return to that same
state. This is useful when you are running a model that takes
some time to equilibrate, but then want to repeat an experiment
starting each time from the same saved state.
In some model scripts, it may be useful to save and restore more
than once. In this case, you must use different file names to
keep track of the appropriate state.
When selecting a file name, remember that if you are running
several simulator processes on the same model simultaneously,
you may want to set a different file name for each separate
simulation. The simulator provides you with several ways to
generate unique file names. The "getpid()" function returns
a 6-digit process number. This number refers to the simulator
process which is the same as the "PID" number printed out by
the "ps" command (see "getpid()" under "Built-in Functions"
below). You can use getpid() to generate a file name like this:
In other cases, you may want to equilibrate a model, then save
its state, and use this state to rapidly start up a different
model that has the same structure (i.e. equilibrates to the same
state) but run different experiments. In this case you may want
to create the save, restore without setting a unique filename.
This will allow many scripts to read the same save file when
restoring to the original file's state.
A statement list enclosed by curly brackets ("{}")
must have a semicolon after it (except between an "if ...
else" statement):
To find an element connected to a node, you can make a
"for" loop to check for the one you are looking for:
Another faster way of doing the same thing, using "numsyn" and
"synapse <expr>":
This statement is useful when building neural circuits
with "developmental rules". When an array of neurons is
made, the algorithm that defines them may not include a
precise location on the dendritic tree for synaptic
connections. Instead, synaptic connection may be defined by
a "connection rule" that specifies how to connect two cells
based on distance and other factors. In this case, new
nodes for connecting the synapses are needed at locations
not specified by the algorithm that made the cell. Thus the
"at <node> : <element>" statement allows the
"connection rule" to make connections wherever it needs to.
When the following statement executes, the variables will
contain the value from the corresponding unspecified
dimensions of the node being considered by the loop. For
example:
If an element type is specfied, without a node, then all
elements of that type are selected. If both element type
and node are specified, then only elements of that type with
nodes that match the specification are selected. For
example:
If you want to erase nodes or elements selectively (see
"erase node" and "erase element"
above) from within a "foreach" statement, you must erase
only the node or element provided by that iteration of
the foreach statement. If you try to erase other nodes
or elements, you may produce undefined behavior. The reason
for this restriction is that the foreach statement cannot
find the next node or element if you erase it.
Arrays can be passed into procedures and functions. The call is
by reference, so that the address of the original array is passed
to the procedure, and any modifications it makes on the array
will appear in the original array outside the procedure. An
array passed into a procedure or function may be assigned to
another array, but it must have the same size.
Functions can return scalar or array values.
You can set a new procedure/function to be equal to a previously defined
one. The assignment is like a function definition, except that
there are no formal arguments or block of statements:
You can define macros (redefine the syntax that NeuronC
understands) using the "nc -C" command-line switch. This runs
the standard C pre-processor that is included with the "gcc"
compiler. The "cpp" pre-processor is run by NeuronC using an
internal pipe to process and expand macros before it is parsed by
the simulator. You can define a macro at the top of a script
file like:
In the example above for the "plot V[]" statement, the "max"
and "min" clauses are required but these are supplied by a macro,
even though they did not originally appear in the required
positions in the statement. The macro changes the text that the
simulator actually sees so you can modify the syntax of the
language. The "include" statement allows the inclusion of a
text file into a NeuronC program, and is useful for
allowing a standard neural circuit definition to be
used in several different models. Note that the "include"
statement must be "external," i.e. it must not be placed
inside a procedure or function. It may be placed inside
an "if" statement, but it must be the only statement inside
the "if". The "system" command allows any standard system command such
as "ls -l" (list directory) or "vi modelfile" (edit a NeuronC
program) to be run. The "system" command is useful when running NeuronC in
interactive mode, but can also be used in a simulation script to
run other commands. For example, you can run a series of
simulation scripts from a parent script:
Some other nice things:
If you have a script that prints a number or a small amount of
text, you can run an nc script several times, each time returning
the output into a variable in the parent script. This method
avoids making any output files, and is appropriate when you want
to run several closely related simulations (e.g. with a different
random seed):
Some examples:
In the compiled version of the simulator, it is necessary
to specify all parameters that will be given on the
command line, so that the simulator can find them and store
the values. [The intepreted version accomplishes this automatically
with its dynamic symbol table allocation.] You can do this by
calling the "setptr()" or "setptrn()" procedures, with the
text name of the variable and a pointer to the variable:
When the array size is not specified, its size is determined
by the initialization:
Any array values not specifically initialized are set to an
undefined value which will generate an error if accessed. That
value is "UNINIT" and you can use it to create an unitialized
value.
dim arr1 [5][2] = {{ 1, 2, 3, 4, 5, 6, 7, 8 }};
print arr1;
1 2
3 4
5 6
7 8
uninit uninit
Arrays can be passed into procedures and functions. The call is
by reference, so that the address of the original array is passed
to the procedure, and any modifications it makes on the array
will appear in the original array outside the procedure. Arrays
can also be passed out on return from functions.
Most operators work on arrays and combinations of arrays and
single valued variables. You can add regular variables and arrays.
When the type is different (string,number or number,string), the
type of the array sets the type of the result:
2D arrays can hold matrix values. Several matrix functions
allow very powerful solutions to matrix equations:
You can find out how many dimensions an array has with the "dims"
statement, and you can find the size of an array with the
"sizeof()" function:
Although the standard initializer is "={{...}};",
you can also initialize an array by writing a procedure like this:
Click here to return to NeuronC Statements
Local arrays are accessed through the stack but their
space is allocated on the heap. A new instance of a local
array is defined each time control enters the block. After
control exits the block in which a local array was defined
the array is erased.
Click here to return to NeuronC Statements
The "printf" statement is identical to the familiar
library subroutine "printf". It prints a formatted string
to the "standard output". It requires a "format" string,
which may contain literal characters and formats of numbers
or strings to be printed. A number format has a "%"
followed by either "f" (floating-point), "e" (with
exponent), or "g" (integer, floating point, or with exponent
whichever takes fewest chars to print out).
The "fprintf" statement is identical to the "printf" statement
except that it prints to a file. The file is defined by a "file
descriptor" which you must define before calling "fprintf",
exactly like in standard C. The file descriptor is created by a
call to "fopen()" (see above). In addition, the file can be
"stdout" or "stderr", exactly like in standard C, except that
these are defined as filenames and must be enclosed in double quotes,
e.g. "stderr". They are normally displayed on the video screen but
can be redirected with shell commands. The file descriptor
can also be a filename if you don't need to keep the file open
between fprintf() calls. Any message printed to "stderr" is
guaranteed to appear on the screen (unless redirected), even
if the program terminates prematurely. This is useful for debugging.
The "sprintf" statement is identical to the "printf"
statement except that it prints its output into the first
argument which is set to string type.
Click here to return to NeuronC Statements
The "sscanf" function is identical to the "scanf" function
except that it reads its output from the first argument which
must be a character string.
The "fscanf" function is identical to the "scanf" function
except that it reads from a file. The file is defined by a "file
descriptor" that you must define before calling "fscanf",
exactly like in standard C. The file descriptor is created by a
call to "fopen()". In addition, the file can be "stdin"
which is normally the keyboard (exactly like in
standard C) but can be redirected with shell commands. The file
descriptor can also be a filename if you don't need to keep it
open between fscanf() calls. "fscanf" returns the number of
arguments converted.
The "fgets" function reads a line from a file, exactly like in
standard C. The parameters are "var", the line buffer, "n", the
maximum size of the line buffer, and "fd" the file descriptor
that has been created by a call to fopen(). If "fd" is "stdin"
then the standard input is read, and if it is a filename, the
file will be opened and read. If successful, "fgets" returns
a 1, and if not it returns 0.
The "fgetc" and "fputc" functions read and write a single
character from a file, exactly like in standard C. If "fd" is
"stdin" then the standard input is read/written to, and if it
is a filename, the file will be opened and read/written to.
The "getflds" function reads a line from a file, and then parses
it into text tokens. The parameter is "fd" the file descriptor,
set by a call to "fopen()". The text tokens are delimited by "
,:\t\n\r" (i.e. the tokens can be separated by spaces, colons,
tabs, LF, CR). It returns the text tokens in an array. The zero'th
element of the array "arr[0]" is the whole line, and the other
elements "arr[1] ... arr[n]" are the individual elements. The size
of the array is the number of tokens. Multiple calls to the same
file (with the same file descriptor fd) will parse
consecutive lines of text in the file. When getflds() gets to the
end of the file, it closes the file and returns with an array of zero
size.
Note that you can use the atof() function to get a numeric value
for numeric tokens:
Comment lines may be included in the "fread" file.
Any line starting with the "#" character is ignored.
Comments are useful for documenting data files.
Click here to return to NeuronC Statements
Click here to return to NeuronC Statements
The "varnum()", "varstr()", and "varchar" functions return a 1 if
a variable is a number, string or char, respectively, otherwise
they return 0. They are useful when checking variables set
on the command line.
You can do this with the "onplot()" procedure. If the
"onplot()" procedure is defined (with the "proc" statement), it
is run at increments of the plot time defined by "ploti" (plot
increment). You can place any commands you like in the
procedure, which has access to any recorded value (voltage,
current, light) or variable. For the compiled version, you
set the name of the onplot procedure with the "setonplot()"
procedure.
The "elap_time" function returns the number of minutes (accurate
to .0001667 min = .01 sec) since the start of the simulation
process. It is useful for timing a part of a simulation run, or
for estimating how a script will take.
The "getpid()" function returns the current process number
of the simulator. This is useful to make a temporary file name
when you are running multiple copies of a script:
The second case shows how to add 4 more random digits onto the file name to
make it even more unique. The "rand()" function is seeded by the "rseed"
variable. This can be set by the script or "-r x" on the command line (see
"rseed" above). To make the "rseed" value different for each simulation run,
set it negative, and it will be set instead by a combination of the process
number and the system time when the simulator first starts up.
The "system_speed()" function returns the approximate CPU
speed. [ You can recalibrate it by following the instructions in
"system_speed()" in "ncmain.cc".] It is useful for estimating how
long a script will take.
The "rand()" function returns a number between 0 and 1.
The "rseed" variable sets the seed for the random number
generator, as does the "-r n" command line switch (See
Section 6). The "gasdev()" function returns a Gaussian
distributed set of numbers with zero mean and unit variance,
and the "poisdev(m)" function returns a poisson rate distribution.
The "gamdev(n)" function returns a gamma interval distribution,
where its order "n" is a positive integer. Note that a gamma
distribution with order 1 is equal to the intervals in a poisson
distribution with mean of 1. To generate a gamma interval
distribution normalized to a mean of 1, use:
where "gorder" is set greater than 1 to generate an interval
distribution more regular than Poisson. This function is used
in the simulator to generate synaptic vesicle release from the
"CoV" synaptic parameter.
If you set "rseed" to a negative number, its value is changed to
a different value every time to randomize the random function
sequences. The seed value is computed from the process ID number
and the system time, but appears in "rseed" only after the script
does a "run" or "step". Similar behavior occurs when you set
"rseed" from the command line switch "-r n", but in that case
"rseed" contains the randomized value after you run the
"setvar()" function.
The "initrand" and "rrand(n)" statements allow you to create
lots of individual random functions that produce different
sequences. First you run the "initrand(n)" statement which
sets up a different random number generator for each "n".
It will automatically seed the generator, but including the
"rsd=x" parameter allows you to specify the seed (see the "rsd"
parameter in the "photoreceptor" statement). The "rgasdev(n)"
function allows you to create an individual Gaussian distribution
in the same way as "rrand(n)" above.
There are five random sequence generators included in the
simulator.
The "taus2" generator (from GSL, http://www.gnu.org/software/gsl)
is one of the fastest random generators available and is good quality.
It has no significant correlations and uses only 12 bytes, and
has a sequence period of 2^88 (10^26).
The "taus113" generator (from GSL, http://www.gnu.org/software/gsl)
has a longer period (2^113, 10^34) is only ~2% slower than taus2
(see https://patchwork.ozlabs.org/patch/290250), and is one of the
highest quality random generators available. It has no significant
correlations and uses only 16 bytes. It is the default random
sequence generator in "nc".
The "taus258" generator (from https://apps.dtic.mil/sti/pdfs/AD1024837.pdf)
has a longer period (2^258, 10^77) is only ~10% slower than taus113,
and is one of the highest quality random generators available
(see https://apps.dtic.mil/sti/pdfs/ADA486637.pdf). It has no significant
correlations but uses 40 bytes.
The "tinymt64" generator (from http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/TINYMT/index.html)
has a longer period than taus113 (2^127, 10^38) is only a little (~40-50%) slower,
and is one of the best good quality random generators available, noting
the tradeoff between speed and length of period. It has no significant
correlations and its state uses only 32 bytes. One of its interesting
features is the use of parameters that can change the sequence, where
the seed sets the start of each sequence. In "nc" the seed sets a different
start and also a different sequence. This can prevent significant correlations
between different noise sequences.
The "mt" generator (from GSL, http://www.gnu.org/software/gsl)
has the longest sequence period (2^19937, 10^6000). It is fast,
a little slower than taus2 (~6-12%) but because of its complexity
its state requires 2500 bytes. Because a state must be saved for
each separate random number sequence in "nc" (i.e. for each
neuron that has an individual random seed set), this is a
significant drawback, but may not be a problem if you have enough
RAM.
The gausnn function is useful for creating arrays of
cells that are randomly placed but have a certain amount of
regularity. This function creates a set of points having a
Gaussian distribution of mean nearest-neighbor distance,
with a given density and degree of regularity within a
specified square region. It is useful from a regularity of
3 (almost random) to a regularity of 50 (almost perfect
triangular packing), although it is most accurate (better
than 5%) for regularities above 5. One can also specify the
mean and standard deviation or various combinations of these
parameters.
The gausnn algorithm attempts to use the information
specified in the most appropriate way and calculates how
many cells should fit in the region specified. If "numcells"
is set, its value will be used to determine the density,
otherwise if "density" is set, its value will be used to
determine the number of cells. If neither of these is set, but
"nnd" (mean nearest-neighbor distance) is set, its value is
used to determine the density and number of cells. If none of
these are set, a default value of 20 um is assigned to "nnd" and
this is used to determine the density and number of cells. In a
similar manner, the regularity of the array can be set with "reg"
(mean/std.deviation), or the "nnstd" parameters.
The number of points successfully placed in the region is
returned. The points are returned in the array (previously
undefined). The array is defined to be a 2-dimensional array
with the first dimension equal to the number of points and the
second dimension 0 for X and 1 for Y. The array can be written
to a file with "fwrite" or used directly by "nc" to create an
array of neurons, etc.
The "rsd" parameter is useful to create an array of neurons whose
positions are not affected by construction of other parts of a
neural circuit. If "rsd" is set to a negative number, its value
is set to a different value every time the simulation is run
(also the default behavior for the simulator's random number seed
"rseed"). If "rsd" is not set, the default random number seed
"rseed" is used.
To see a visual display of gausnn(), you can run something like this:
The function you want to fit "fit_func" must be a function of 2 arguments,
1) the X-axis value, and 2), an array containing the coefficients to be fitted
for the function. You set the initial values of the coefficients (they
must not all be zero). You can set constraints on the coefficient values by
including range checks in the function (see example below).
(interpreted:)
A 2D version of lmfit, called "lmfit2d()" is also available.
It is similar to the standard 1D version except that the data
array has the X,Y values sequentially stored in the first
dimension, and the second dimension contains the Z values for
fitting.
A test program for 2D fitting called "gaussfit.cc" is provided.
It reads in a square array of values from a file and allows
you to set initial values for 6 parameters from the command line:
Click here to return to NeuronC Statements
A frame is a name for a subregion of a window that can be
rotated, translated, and scaled separately from its parent.
The frame statement causes the named frame to be the current
one. If the named frame doesn't exist, then it is created
new. If it does already exist as a parent or descendent of
the current frame, the current frame is moved appropriately.
gsize sets the size of a frame as a fraction of the current
frame. This is useful to allow the other graphics
statements to scale to the same size as the "display"
statements in "nc".
gcrot (calib in radians) rotates only text (not graphics)
about the current location. gdash causes a line to be dashed
with a certain pattern (0 - 8 are different patterns).
Example:
(interpreted:)
(interpreted:)
(interpreted:)
Aperture and spatial filtering
For simplicity of computation, a photoreceptor is a
"point receiver", i.e. for the purposes of spatial summation
it has an aperture of zero. The diameter used to calculate
photon flux does not imply an additional convolution beyond
the convolution for optical blur. For many simulations,
this is not a problem because the diameter of optical blur
is substantially greater then the photoreceptor aperture.
In this case, an aperture would add a negligible spread to
the optical blur point-spread function.Save, restore photoreceptors
When repeating a stimulus several times during a
simulation, it is often useful to "reset" a simulation's
state to what it was before the stimulus. The "save"
parameter causes the photoreceptor to save the current
values of its internal biochemical difference equations.
Later, a duplicate photoreceptor statement with the
"restore" parameter set causes the photoreceptor to retrieve
the previously stored values immediately. In order to
access the original photoreceptor, the "save" and
"restore" parameters must be used with the "ename" and
"modify" commands.
(interpreted:)
dim ncone [100];
at n cone (50,0) attf .75 ename ncone[i];
.
.
.
modify ncone[i] cone () save;
code for stimulus here.
.
step xtime;
.
code for recording response here.
.
modify ncone[i] cone () restore;
(compiled:)
int ncone [100];
photorec *p;
p= make_cone(nd(n)); p->xloc=50; p->yloc=0; p->attf=.75; ncone[i]=p->elnum;
.
.
.
p=make_cone(nd(0));
p->modif = ncone[i]; p->save = 1;
code for stimulus here.
.
step (xtime);
.
code for recording response here.
.
p=make_cone(nd(0));
p->modif = ncone[i]; p->restore = 1;
The element number of the original photoreceptor is saved
in the array "ncone[]" and this number is used to access the
element later in the program. The "save" is placed just
before the stimulus, and the "restore" is placed just after
the response has been recorded.Difference equations
The photon flux is the input to a set of
difference equations which are derived from the transduction
scheme of Nikonov et al (1998). This transduction
mechanism simulates the initial phase of the biochemical
cascade from rhodopsin through G-proteins to
phospodiesterase, cyclic-G and finally the light-modulated
conductance. In addition there are 4 difference equations
which simulate the calcium-feedback control of the recovery
phase (see Nikonov et al. 1998). These difference
equations are integrated with the Euler method with a
constant timestep of 0.1 msec.
(interpreted:)
plot G(n) <element expr>
G(0) conductance
G(1) isomerized rhodopsin
G(2) meta rhodopsin I
G(3) meta rhodopsin II (R*) activates G protein
G(4) G protein
G(5) PDE
G(6) G cyclase
G(7) cGMP
G(8) Ca feedback for recovery and adaptation
G(9) Cax (protein between Ca and G cyclase)
G(10) Rhodopsin kinase (turns off rhod in response to decrement in Ca)
For mouse rod (Invergo et al. 2014), pigm=24:
G(1) conductance
G(1) isomerized rhodopsin
G(2) rhodopsin bound to G protein
G(3) rhodopsin bound to rhodopsin kinase
G(4) activated G protein bound to ATP
G(5) activated PDE
G(6) activated RGS-PDE-G protein complex
G(7) cGMP
G(8) Rec protein bound to Ca2+
G(9) Free Ca++
G(10) Buffered Ca++
G(11) rhodopsin kinase (turns off rhodopsin)
(compiled:)
plot (G, n, <elnum>,<max>,<min>);
Where: n=0-10 (as above).
elnum = ename, element number.
max, min = max and min for plot.
Click here to return to Photoreceptor statement index
Pigment sensitivity functions
0 primate rod
1,2,3 primate cone L,M,S
4,5,6 turtle L,M,S
10,11,12 rabbit R,M,S
13,14,15 guinea pig R,M,S
16,17,18 goldfish
19,20,21 van_Hateren cone with adaptation (2007)
22,23 mouse M,S cone
24 mouse rod with adaptation from Invergo et al (2014)
25 human S cone (for human L,M cones use primate)
26 mouse channel-rhodopsin-2 from Williams et al (2013)
100 simple
default 1 ->cone
Rod and cone type pigments are specified with the "pigm"
parameter. The first 4 pigment sensitivity functions (rod=0,
l,m,s = 1,2,3) are from Baylor, et al, 1984 and 1987 (monkey) and
operate between 380 and 800 nm. The functions are implemented
using a lookup table with values every 5 nm, quadratically
interpolated between points. Default path length is dependent on
pigment type: rods have a 25 um path, L, M and S cones
35 um path. These can be overridden using the "pathl=x" parameter.
The absolute sensitivity of a photoreceptor is calculated from
tables of specific density vs. wavelength, multiplied by the path
length. This calculation takes into account the photoreceptor's
absolute density and its consequent self-screening.
G = Isat / (Iflux + Isat)
Where: Isat = 50000 R*/sec [for cones]
500 R*/sec [for rods]
This provides a simple intensity response and allows photon noise
but has no temporal filtering action. All the efficiency factors
and pigment absorption factors are taken to be the same as in
monkey "L" (red-absorbing) cones.
sod = function of pigment and wavelength (table lookup)
od = sod * path length
T = exp10 ( -od )
Labs = photons/sec * ( 1 - T ) * mfilt * attf * dqeff
Where:
sod = specific optical density (extinction coeff. x concentration)
od = optical density
T = fraction Transmitted light
mfilt = macular filter (if defined, 1.0 by default)
attf = miscellaneous attenuation factor (set in photrec only, default 0.9)
dqeff = default quantum efficiency (global variable "dqeff", set at .67)
Labs = Light absorbed (absolute sensitivity)
Voltage follower
(interpreted:)
conn <node> to <node> vbuf <options>
conn <node> to <node> vbuf gain=<expr> offset=<expr> tau=<expr> delay=<expr>;
(compiled:)
vbuf *make_vbuf (node *node1, node *node2, double offset, double gain, double delay, double tau)
or
vb = (vbuf *)conn(ct1, cn1, nd1, ct2, cn2, nd2, BUF);
vb->offset = offset;
vb->gain = gain;
vb->tau = tau;
Where:
option units: default:
gain 1 Gain, Vout = (Vnode1 - Voffset) * gain
offset V 0 Voltage offset
tau sec 0 Low past time const in sec.
delay sec 0 Time delay in sec.
A "vbuf" is a connection between two nodes that causes the
voltage at the second node to exactly duplicate the voltage at the
first node. In effect, it functions as a voltage clamp but also has
the ability to function as an amplifier (op-amp).
Channel statement
Click here to return to NeuronC Statements
Channel
(interpreted:)
at <node> chan Na type <expr> 'parameters'
at <node> chan K type <expr> 'parameters'
at <node> chan CGMP type <expr> 'parameters'
at <node> chan Ca type <expr> 'parameters' 'caexch params' 'pump params' 'cicr params' 'ip3 params'
at <node> cacomp 'Ca parameters' 'caexch params' 'pump params' 'cicr params' 'ip3 params'
(compiled:)
elem *e;
chattrib *c;
cattrib *ca;
e = at (nd(<node>), CHAN);
a = make_chan (e, Na, <expr>); 'parameter code'
a = make_chan (e, K, <expr>); 'parameter code'
a = make_chan (e, cGMP, <expr>); 'parameter code'
ca = (cattrib*)make_chan (e, Ca, <expr>); 'parameter code'
ca = (cattrib*)make_chan (e, CACOMP,<expr>); 'parameter code'
parameters: default:
--------------------------------------------------------------------
(interpreted:)
vrev = <expr> .04 V (Na) (~vna) Na reversal potential (Volts)
-.08 V (K) (~vk) K reversal potential (Volts)
.05 V (Ca) from cao/i and [K]i
offsetm = <expr> 0.0 V (dnaoffsm) relative threshold for Na chan activation (Volts)
offseth = <expr> 0.0 V (dnaoffsh) relative threshold for Na chan inactivation (Volts)
offsetm = <expr> 0.0 V (dkoffsm) relative threshold for K chan activation (Volts)
offseth = <expr> 0.0 V (dkoffsh) relative threshold for K chan inactivation (Volts)
offset = <expr> 0.0 V (dcaoffs) relative threshold for Ca chan activation (Volts)
tau = <expr> 1.0 relative act & inact 1/rate.
taum = <expr> 1.0 (dnataum) relative activation 1/rate.
taun = <expr> 1.0 (dktaun) relative activation 1/rate.
tauh = <expr> 1.0 (dnatauh) relative inactivation 1/rate.
taua = <expr> 1.0 relative activation alpha 1/rate.
taub = <expr> 1.0 relative activation beta 1/rate.
tauc = <expr> 1.0 relative inact 1/rate.
taud = <expr> 1.0 relative inact recovery 1/rate.
taue = <expr> 1.0 relative flicker 1/rate.
tauf = <expr> 1.0 relative flicker 1/rate.
maxcond= <expr> 1e-9 S (dmaxna) maximum conductance (Siemens)
2e-10 S (dmaxk)
1e-10 S (dmaxca)
density= <expr> no default membrane chan density (S/cm2).
ndensity=<expr> no default membrane chan density (N/um2).
N = <expr> no default Number of channels.
unit = <expr> (set by chan type) Unitary channel conductance
caperm = <expr> (set by chan type) rel Ca permeability (NMDA,ACH,AMPA,cGMP).
cakd = <expr> 1e10(=none)(dcakd) Kd for Ca binding to block channel.
cahc = <expr> 1 (dcahc) Hill coefficient for Ca binding.
k1 = <expr> 1e-7 M (dsk1), 1e-6 (dbk1) mult for Ca sens of KCa type 0,1,2,3 chan (KCa)
k2 = <expr> 1e-7 M (dsk2), 1e-6 (dbk2) mult for Ca sens of KCa type 0,1,2,3 chan (KCa)
d1 = <expr> 0 (dsd1), 1 (dbd1) mult for volt sens of KCa type 0,1,2,3 chan (KCa, type SK, BK)
d2 = <expr> 0 (dsd2), 1 (dbd2) mult for volt sens of KCa type 0,1,2,3 chan (KCa, type SK, BK)
cao = <expr> 0.005 M (dcao) extracellular Calcium conc (Molar)
cai = <expr> 50e-9 M (dcai) intracellular Calcium conc (Molar)
tcai = <expr> 10e-9 M (dtcai) intracellular Calcium conc threshold (Molar)
cbound = <expr> 5 (dcabnd) ratio of bound to free Ca
cshell = <expr> 10 (dcashell) number of int Ca diffusion shells
caoshell = <expr> 10 (dcaoshell) number of ext Ca diffusion shells
cabuf off use Ca buffer
kd = <expr> 1e-6 M (dcabr/dcabf) Kd for Ca buffer (rev/forw rates)
vmax = <expr> 1e8 /M/s (dcabf) Forward rate for Ca binding buffer
btot = <expr> 3e-6 M (dcabt) Buffer concentration in shells
btoti = <expr> 30e-6 M (dcabti) Buffer concentration in first shell
caexch off use Na-Ca exchanger
kex = <expr> 5e-9 A/mM4/cm2 (dcakex) exchanger current density
capump off use Calcium pump
vmax = <expr> 1e-4 A/cm2 (dcavmax) pump maximum velocity
km = <expr> 2e-7 M (dcapkm) pump 1/2 max conc
cicr off use Calcium-induced calcium release
cas = <expr> 1.6e-6 M (casStart) CICR [Ca] init
vm2 = <expr> 65e-6/ms (vm2CICR) CICR maximum uptake velocity
vm3 = <expr> 500e-6/ms (vm2CICR) CICR maximum release velocity
kf = <expr> 5e-6/s (kfCICR) CICR leak rate
k2 = <expr> 1e-6 M (k2CICR) CICR thresh uptake
kr = <expr> 2e-6 M (krCICR) CICR thresh release
ka = <expr> 0.9e-6 (kaCICR) CICR thresh release
ip3 off use IP3 internal store
cas2 = <expr> 1.6e-6M (cas2Start) IP3 [Ca] init
ip3i = <expr> 0.4e-6M (ip3iStart) IP3 [IP3] init
vip3 = <expr> 7.3e-6/s (v1IP3) IP3 static flux rate
bip3 = <expr> 0.31 (betaIP3) IP3 static frac
chnoise = <expr> 0 (off) = 1 -> set channel noise on
N = <expr> set by unitary cond Number of channels
unit = <expr> (set by chan type) Unitary channel conductance
rsd = <expr> set by rseed,srseed random seed
(compiled:)
elem *e;
chattrib *c;
cattrib *ca;
nattrib *n;
e = at (nd(<node>), CHAN);
e = make_sphere(nd(soma),dia=10);
ca = (cattrib *)make_chan(e,cGMP); ca->pump=1; ca->vmax=<expr> ...
ca = (cattrib *)make_chan(e,CACOMP); ca->pump=1; ca->vmax=<expr> ...
ca = (cattrib *)make_chan(e,CACOMP); ca->cicr=1; ca->vm3=<expr> ...
n = make_chnoise(e); n->unit=<expr> ...
These statements define a macroscopic conductance at a node.
Several classes of ion-selective channels can be created: Na, K,
Ca. Within each class there are several types. Type 0 is the
Hodgkin-Huxley (1952) standard type. Type 1 is a
discrete-state version of the H-H type, and other types have
different behavior (see below). Type 0 channels' conductance is
the product of activation (m or n) and inactivation (h) variables
in the form m3h for Na, and n4 for K. Standard rate
constants (alpha, beta) are calculated from look-up tables
generated at the beginning of each run, based on the temperature
(set by "tempcel") and a Q10 set by a default variable (see
below).Setting the channel conductance
There are several ways to set the channel conductance. To set
the absolute conductance, use the "maxcond" parameter. To set a
channel density, use the "density" or "ndensity" parameters. If
you know how many channels you would like, use the "N" parameter.
These parameters can be set in conjunction with the "chnoise"
parameter to define noise properties (see "Markov channel noise"
below).Voltage offset parameters
The "offset(m,h)" parameters define a voltage offset in the
channel voltage gating properties relative to the default value
(normally 0). The "offsetm" and "offseth" parameters modify the
activation and inactivation voltages, respectively, and the
"offset" parameter changes both. The default value represents
the standard activation (i.e. 0 = no offset) defined by Hodgkin
and Huxley. You can change the channel's activation level by
selecting a different threshold. For example, by using a more
positive "offsetm" for a sodium channel, the channel will
activate at a more positive voltage and action potentials will
occur at a slower rate. A more negative sodium threshold can
increase the frequency of action potential firing.Tau parameters
The "tau" parameters control the amplitude of the rate
constants alpha and beta for each of the control variables
m,h (for sodium), and n (for potassium), (m for calcium).
They are "relative" parameters, meaning that the number you
set is normalized by the parameter's default value and the
resulting quotient multiplies the (in)activation rate
constant.
base_tau = time constant you find for default tau
actual rate = rate * base_tau / tau
"taum" corresponds to the sodium activation time constant, "tauh"
corresponds to sodium inactivation, and taun corresponds to
activation of potassium. If you want to change all of the rates
proportionately, set the "tau" parameter.Functions to plot Minf, Mtau, Tau[a-f]
Each channel defined in a simulation can have different rate
multipliers and voltage offset selected by the user. To plot these,
there are several predefined functions. They include the voltage
offsets and tau[a-f] parameters included in the channel's definition:
minf (v, ename); /* returns equilibrium value of "m" */
mtau (v, ename); /* returns time constant of "m" */
hinf (v, ename); /* returns equilibrium value of "h" */
htau (v, ename); /* returns time constant of "h" */
ctaua (v, ename); /* returns time constant of alpham */
ctaub (v, ename); /* returns time constant of betam */
ctauc (v, ename); /* returns time constant of alphah */
ctaud (v, ename); /* returns time constant of betah */
ctaue (v, ename); /* returns time constant of flicker */
ctauf (v, ename); /* returns time constant of flicker */
Click here to return to Channel statement index
Temperature dependence (rates, conductances)
The rates and conductances of voltage-gated channels changes
with temperature in a predicatable way. The change is specified
with a "Q10" which is the change in rate over a 10 degree change
in temperature. Q10 values of between 1.4 and 3 are common. A
high value of a Q10 implies a high activation energy (Ea) for the
corresponding chemical reaction. This can be calculated from the
time constant of channel activation:
Ea = [(R T1 T2) / (T2-T1)] ln (tau1/tau2) (see Kirsh and Sykes, 1987)
Q10 = exp (10 Ea / (R T1 T2) (method of computing Q10)
Where:
R = gas const, 1.987 cal/deg/mol.
T1,T2 = Temperatures, deg K.
tau1 = time constant of channel at T1.
tau2 = time constant of channel at T2.
Once the Q10 value for a temperature sensitive function (rate or
conductance) is known, the function is multiplied by a factor
defined by the Q10 equation:
rate multplier = exp(log(dqx) * (tempcel - dbasetc) / 10)
Where:
dqx = the Q10 temperature dependence (dqm=2, dqh=3, dqc=1.4, etc.)
tempcel = temperature of the simulation
dbasetc = base temperature for channel, default = 22 deg. C.
The temperature dependence of most of the rate functions is set
to a default Q10 value of 3, as assumed by Hogkin and Huxley
(1952), except for alpham and betam which are set to a default of
2, and for alphan, 3.2, and for betan, 2.8 (Frankenhaeuser and
Moore, 1963).
The default values are:
dqm = 2.3 (alpham, betam)
dqh = 2.3 (alphah, betah)
dqna = 2.3 (alphan)
dqnb = 2.3 (betan)
dqn = 2.3 (alphan,betan) (set this to override dqna, dqnb)
dqca = 3 (alphac, betac)
dqd = 3 (alphad, betad, for KA h)
dqkca = 3 (for Kca chan)
dqsyn = 3 (synaptic channels)
dqcab = 2 (Ca buffer)
dqcavmax=2 (Ca pump)
dqdc = 1.3 (Ca diffusion constant)
dqc = 1.4 (channel unitary conductance)
dqrec = 2.7 (photorecptor transduction shape, not currently used)
dqcrec = 1.8 (photorecptor transduction cond)
dqrm = 1 (membrane conductance 1/Rm)
dqri = 1 (axial conductance 1/Ri)
For each channel type the rate function is defined at a certain
temperature (the "base temperature"). At other temperatures the
rate is multiplied by the increase or decrease calculated from the
Q10 over the change in temperature from the original definition.
Since voltage gated channels have a well-known temperature
depency, it is always used, even when you specify a change in
rate (with the dividers "taum", "tauh", etc.) from the
original absolute rate.
var default meaning
------------------------------------------------------------------------------
dbasetc 22 deg C base temp for membrane channel kinetics, conductances
dbasetsyn 22 deg C base temp for synaptic kinetics
dbasetca 22 deg C base temp for ca pumps
dbasetdc 22 deg C base temp for Ca diffusion constant
Normally it is not necessary to change the base temperature for
channel kinetics because the rate functions are automatically
adjusted when you change temperature (with the "tempcel"
parameter).
var default Q10 meaning
------------------------------------------------------------------------------
dratehhm 2.9690 2.0 multiplier for normalizing alpham, betam from 6.3 to 22 deg C
dratehhh 5.6115 3.0 multiplier for normalizing alphah, betah from 6.3 to 22 deg C
dratehhna 6.2099 3.2 multiplier for normalizing alphan from 6.3 to 22 deg C
dratehhna 5.0354 2.8 multiplier for normalizing betan from 6.3 to 22 deg C
These values are computed from the Q10 equation:
dbasehhh = exp(log(3.0) * (22 - 6.3) / 10)
The temperature sensitivities for channel gating and conductance
have recently been determined for mammalian ganglion cells by
Fohlmeister, Cohen and Newman (2009). They are nearly constant
from 22 deg C to 37 deg C, but below 22 deg the changes are
larger, and below 10 deg C they are much larger. To work in the
range of 10-22 deg, you can set dqm, dqh, and dqn to 3.5.
chan default Q10 Q10
@22-37deg @10-22 deg
Gating
dqm 2.3 1.95 3.5 (alpham, betam)
dqh 2.3 1.95 3.5 (alphah, betah)
dqn 2.3 1.9 3.5 (alphan, betan)
dqca 2.3 1.95 3.5 (alphac, betac)
conductance
dqc(Na) 1.44 1.85 3.0 (channel unitary conductance)
dqc(K) 1.44 1.8 3.5 (channel unitary conductance)
dqri 1.0 0.8 (axial conductance 1/Ri)
dqrm 1.0 1.85 (membrane conductance 1/Rm)
You can set these values according to the temperature ("tempcel")
by calling the function:
(interpreted:)
set_q10s()
(compiled:)
setq10s()
which returns the current temperature ("tempcel");
For the calcium buffer and pump the Q10 has been arbitrarily set
to 2. The rates will change with temperature only when the
default rates for the buffer and pump are used, i.e. if you
specify a rate, it will not change with temperature.
dqcab = 2 (Q10 for Ca buffer)
dqcavmax = 2 (Q10 for Ca pump)
When a unitary conductance for a channel is not specified by the
user, a default value defined for the channel type is used. The
default rate changes according to the temperature and the Q10 set
by "dqc". If you specify a unitary conductance, this value is
used directly, i.e. it will not change with temperature.
unitary conductance = dxu * exp(log(dqc) * (tempcel - dbasetc) / 10)
Where:
dxu = default unitary conductance for the channel (dnau, dku, etc.)
dqc = Q10 for unitary conductances, default = 1.4
tempcel = temperature of the simulation
dbasetc = base temperature for channel, default = 22 deg. C.
Unitary conductances reported in the literature generally have a
Q10 between 1.3 (for diffusion in water) to 1.6, so the value of
1.4 is a compromise (it can be changed for any channel in the
source code). Setting unitary conductance and N
You can define the unitary conductance of the channel in
several ways. You can define it with "unit". Or if you have
defined "maxcond" and "N", the unitary conductance will be
calculated. If you don't define "N", you can set it from "ndensity",
and the resulting value for N will be used with the "unit" value
that you set or with the channel's default unitary conductance.
chan .... chnoise=1 N=25 unit=10e-12
N = you define
unit = you define
channel conductance is then calculated as = N * unit
If you define "N" but not "unit" or "maxcond", the
conductance will be determined from the N you set along
with the default "unit" for the channel type:
chan .... chnoise=1 N=25
N = you define
unit = default for channel
channel conductance is then calculated as = N * unit
If you place the "N" parameter before or without "chnoise", it
will define the channel conductance. You can place a second "N"
after "chnoise" and it will define N for the noise properties
only.
chan .... N=100 chnoise=1 N=25
N = you define
unit = default for channel
channel conductance is calculated as = N * unit
Noise is calculated from second N (25).
Note that you can turn off noise by setting "N" or "chnoise" to zero.
chan .... ndensity=10 chnoise=1
ndensity = you define
unit = default for channel
N is calculated as = ndensity * membrane surface area
channel conductance is calculated as = N * unit
Noise is calculated from N (from ndensity).
If you use a channel's default unitary conductance (by not
defining "unit"), the unitary conductance will have a temperature
dependence (Q10 set by "dqc", default=1.4) caperm parameter
The "caperm" parameter sets the relative permeability
to Ca++ ions. If you specify a value for caperm when
defining a channel, this value will override the default
channel permeability for Ca++. Several types of synaptic
channel (e.g. NMDA-, AMPA-, ACH-, and cGMP-gated channels) carry
about 10-20% of their conductance as Ca++ ions, and this Ca
flux is thought to be important for controlling postsynaptic
mechanisms. If caperm is set (either individually or by
default) for a channel, its Ca current will be automatically
connected to the local calcium diffusion mechanism.
Channels that can be specified alone such as Ca or second-
messenger types such as cGMP-gated can have "calcium
parameters" to define a calcium compartment, but you may
also define one with the "cacomp" statement.Channel types: type 0, Hodgkin-Huxley
Type O channels are derived from the original Hodkgin and
Huxley (1952) papers, and diagrams that precisely match
Hodgkin-Huxley kinetics. Rate functions are the standard alpha
and beta values. The rate functions are placed in tables so
their values can be found efficiently. If you add noise to a
type 0 channel, a 2-state Markov machine is added to the
conductance. This may change the kinetics some depending on the
time constant for the noise ("tauf") you choose (see "Markov
channel noise" below).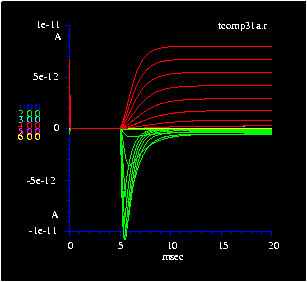
Na type 0 rate functions:
Given Vm in mV, calculate rate /sec:
Activation:
alpham = taum ( -100 (V- -40.) / (exp ( -0.1 (V- -40.) - 1))
betam = taum ( 4000 exp ((V- -65) / -18.))
alphah = 70 exp ((V- -65) / -20.)
betah = 1000 / (exp (-0.1(V - -35)) + 1.0)
Inactivation:
alphah = tauh ( 70 exp ((V- -65) / -20.))
betah = tauh (1000 / (exp (-0.1(V - -35)) + 1.0))
Where:
V = Vm - voffset
voffset = voltage voffset (set by user)
taum = activation rate function divider (set by user)
tauh = inactivation rate function divider (set by user)
Click here to return to Channel statement index
List of all channel types
Channel types
ion type states characteristics
Na 0 0 Standard Hodgkin-Huxley kinetics, m3h.
1 8 Standard Hodgkin-Huxley kinetics,
Markov discrete-state.
2 9 NaV1.2, Markov, modified from Vandenberg and Bezanilla, 1991
3 12 NaV1.2, Markov, from Kuo and Bean (1994).
4 12 NaV1.2, Markov, persistent, from Taddese and Bean (2002).
5 9 NaV1.1, Markov, SCN1A, slow recovery from inactivation,
from Clancy and Kass (2004).
6 13 NaV1.6, Markov, persistent, rapid recovery from inactivation,
from Raman and Bean (2001).
8 9 NaV1.8, Markov, TTX-resistant, similar to type 2 but slower
20 6 Simple Markov, similar to Type 1.
21 2 Integrate-and-fire, Markov.
K 0 0 Standard Hodgkin-Huxley kinetics, n4, non-inactivating.
1 5 Standard Hodgkin-Huxley kinetics, Markov discrete-state
2 0 KA channel, inactivating, HH-type, n3h.
3 8 KA current, inactivating, HH-type, Markov discrete-state
4 3 Ih channel, hyperpolarization-activated, depolarizing
from Hestrin (1987), see chank4.cc.
5 3 Kir channel, hyperpolarization-activated, hyperpolarizing
6 5 Duplicate of type 1 Markov, used for slower version
7 5 Duplicate of type 1 Markov, used for slower version
8 10 HCN (Ih) channel, from Altomare et al. (2001), see chank4.cc.
9 6 HCN (Ih) channel, like Altomare et al. (2001), but only 1 cond state.
KCa 0 0 SKCa, Hodgkin-Huxley-like, no voltage sensitivity.
1 2 SKCa, Markov discrete-state.
Ca-sensitivity can be varied, see below.
2 0 BKCa Hodgkin-Huxley-like.
3 2 BKCa channel, Markov discrete-state.
Voltage- and Ca-sensitivity can be varied, see below.
4 6 SKCa channel, Markov discrete-state,
from Hirshberg et al. (1998).
5 6 SKCa channel, Markov discrete-state,
from Sah and Clements (1999). Insensitive to apamin.
6 10 BKCA channel, Markov discrete-state, voltage sensitivity,
from Cox et al. (1999). (Best BK model yet)
ClCa 1 12 ClCa, like KCa type 4, after Lalonde Kelley, Barnes (2008)
ClCa 2 12 ClCa, like type 1 but senses [Ca]i shell set by "dsclcac" (default 10)
Ca 0 0 L-type Ca, c3 (high voltage activated, tonic)
Ca 1 4 L-type Ca, discrete state, like type 0.
Ca 2 0 T-type Ca, c2h, (low voltage activated, fast inactivating)
Ca 3 6 T-type Ca, discrete state, like type 2.
Ca 4 0 T-type Ca, c3h, (low voltage activated, fast inactivating)
Ca 5 8 T-type Ca, discrete state, like type 4.
Ca 6 12 T-type Ca, low threshold, from Serrano et al, 1999
Ca 7 12 T-type Ca, low threshold, modified after Lee et al., 2003
cGMP 1 8 cGMP-gated chan from rod outer segment (Taylor & Baylor 1995)
cGMP 2 9 cGMP-gated chan, inhibited by Ca binding
AMPA 1 7 AMPA-gated chan, zero Ca perm (Jonas et al 1993)
AMPA 2 7 AMPA-gated chan, Ca perm, independent gating (Jonas et al 1993)
AMPA 3 9 AMPA-gated chan, Ca perm, (Raman and Trussel 1995)
AMPA 4 9 AMPA-gated chan, Ca perm, (simple state diagram, based on Jonas 1993)
AMPA 5 9 AMPA-gated chan, Ca perm, (non-desensitizing, based on Jonas 1993)
ACH 1 5 Acetylcholine-gated chan (Keleshian, Edeson, Liu and Madsen, 2000)
GABA 1 5 GABA-gated chan (Busch and Sakmann, 1990)
GABA 2 7 GABA-gated chan (based on AMPA chan Jonas et al 1993)
GABA 3 7 GABA-gated chan (based on Jones and Westbrook 1995)
GABA 4 5 GABA-gated chan, GABA-C, longer decay (mod. from Busch and Sakmann, 1990)
GLY 1 5 GLY-gated chan (based on GABA chan, Busch and Sakmann, 1990)
The type 1 Na channel has an 8 state transition table with four
inactivated states. The K channel has 5 states with no
inactivated states. They produce identical results to the HH (or
type 0) channels, but run a little slower. The type 2 Na channel
has "improved" kinetics that are defined by a 9-state Markov
diagram. It is the "extended type 3" model of Vandenberg and
Bezanilla, (1991) and is more biologically accurate than HH type
models. It is slightly modified from the published version to
have a higher slope on the activation vs. voltage curve. This
reduces the amount of activation at voltages hyperpolarized from
-50 mV. The type 3 Na channel is from Kuo & Bean (1994) and has
a 12 state transition table with 6 activated and 6 inactivated
states, and is also more realistic than the HH (type 0) channel.
The Na type 4 channel is from Taddese & Bean (2002) and is
a "normal" current that persists to allow pacemaking.
The Na type 6 channel is from Raman & Bean (2001) and is
a persistent current that reactivates rapidly to give burstiness.
The Na type 21 channel is an "integrate-and-fire" model (see
below).
Channel types: type 1
Type 1 channels are derived from "Markov" discrete-state
diagrams that very closely match Hodgkin-Huxley kinetics. Rate
functions are the standard alpha and beta values. The
conductance is normally zero or a small fraction for all the
closed or "inactivated" states.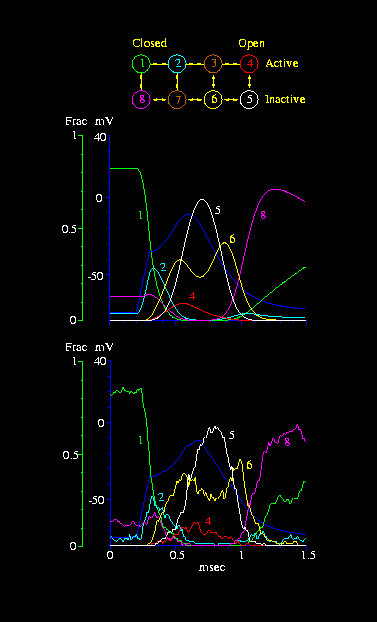
KA (fast inactivating K channel)
The K type 2 channel is an inactivating version of the standard
delayed rectifier K channel. It is described by a m3h kinetic
scheme like the Type 0 Na channel. The K type 3 channel is a
discrete-state version with eight states. It is useful when an
accurate representation of the noise properties of the KA channel
is required.
KA rate functions:
Given Vm in mV, calculate rate /sec:
Activation:
y = -0.1 * (V+90);
alphan = taun * 10.7 * y / (exp(y) - 1)
betan = taun * 17.8 * exp ((V+30) / -10.)
Inactivation:
alphad = tauh * 007.1 * exp (-0.05 * (V+70))
betad = tauh * 10.7 / (exp (-0.1 * (V+40)) + 1.0)
Where:
V = Vm - voffset
voffset = voltage voffset (set by user)
taun = activation rate divider (set by user)
tauh = inactivation rate divider (set by user)
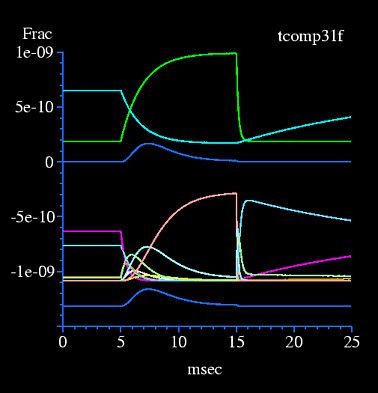
KCa (calcium-activated potassium channel)
The KCa channel types 0,1,2,3 are a calcium-sensitive
potassium current that can be voltage sensitive, modeled after
Hines, 1989 and Moczydlowski and Latorre, 1983. It is a Hodgkin-
Huxley style channel with first-order rate equations alpha and
beta which are voltage and calcium dependent:
Gk = maxcond * n
dn/dt = alphakca - (alphakca + betakca) * n
alphakca = taun / (1 + k1 / [Ca] * exp(d1 * -V / 10) )
betakca = taun / (1 + [Ca]/ (k2 * exp(d2 * -V / 10) ) )
Where:
d1, d2 are voltage coefficients
k1, k2 are calcium coefficients
V = membrane voltage in mV
V = Vm - voffset (set by user)
taun = rate divider (set by user)
The constants maxcond, tau, voffset, d1,d2,k1,k2 can be
specified by the user. The d1 and d2 constants set the voltage
sensitivity, and k1 and k2 set calcium sensitivity.
ClCa (calcium-activated chloride channel)
The ClCa channel is a calcium-sensitive chloride channel found in photoreceptor
terminals near the calcium channels that modulate vesicular release. The ClCa
type 1 channel is modeled after the KCa type 4 channel, except that it has
12 states and its voltage sensitivity is controlled by "dclcavs" (default=2.0)
which multiplies the forward rate of binding by [Ca]i at the first Ca shell
over the range of 120 mv, starting at -40 mV.
Ih channel (activated by hyperpolarization)
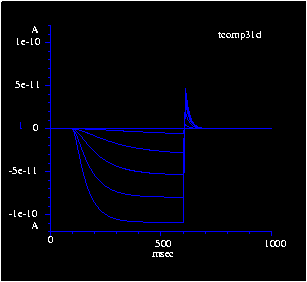
Kir channel (activated by hyperpolarization)
The K type 5 channel is a sequential-state version of the
Kir channel in the membrane of horizontal cells in goldfish
(Dong & Werblin). It is activated when the membrane hyperpolarizes
beyond -40 mV, and has a relatively fast activation time constant. It is
similar to Ih (K type 4 above) except that it has a reversal
potential of -70 mV. Integrate-and-Fire Na channel
The Na type 21 channel is a 2-state channel whose alpha and
beta rate functions integrate a compartment's voltage and
turn on the channel when the integration reaches a
threshold. The "offsetm" parameter defines the zero point
for the integration, for example if set to -0.07 then the
channel will integrate the voltage above -70 mV. After the
channel reaches threshold, it opens its conductance for a
short time (1-2 msec) and resets the integration allowing
the integration to start for the next interval.Calcium channels
Several types of calcium channel are implemented. Two types
(0,2) are based on the Hodgkin-Huxley style of first-order rate
constants:
Type 0 Gca = c3 * maxcond = L-type calcium
dc/dt = alphac - (alphac + betac) * c high threshold
Type 1 same as type 0 but Markov sequential-state
Type 2 Gca = c2h * maxcond = T-type calcium
dc/dt = alphac - (alphac + betac) * c low threshold
dh/dt = alphah - (alphah + betah) * h
Type 3 same as type 2 but Markov sequential-state
Type 4 Gca = c3h * maxcond = T-type calcium
dc/dt = alphac - (alphac + betac) * c low threshold
dh/dt = alphah - (alphah + betah) * h
Type 5 same as type 4 but Markov sequential-state
Type 6 Markov 12 states = T-type calcium
From Serrano et al (1999), low threshold
J Gen Physiol 114:185-201
Type 7 Markov 12 states = T-type calcium
Like Serrano et al, but modified low threshold
for retinal ganglion cell.
Taken from Lee SC, Hayashida Y, and Ishida AT
(2003), J Neurophysiol 90:3888-3901.
The alpha and beta rate equations are similar to those
for the Na conductance (look in "initchan.c" for "accalc()"
and "bccalc()").
Calcium compartment
Whenever a calcium channel is specified, a "calcium
compartment" is generated that is linked to the voltage
compartment, modeled after Hines, 1989 and Yamada et al.,
1989. If several calcium channels are defined at the same
location, they share the calcium compartment.
Calcium buffering
Static buffering is selected with the "cbound" paramter.
It represents the ratio of the bound calcium to the free
concentration. When "cbound" is a large value ( > 50) the
concentration of calcium is much lower and less calcium is
available for diffusing through the shells.
f>
Ca + B <--------> Ca.B
<r
You specify the forward (binding) and reverse (unbinding") rates
(default values "dcabf", "dcabr") using the "kd" (= ratio of
reverse/forward rates) and "vmax" (=forward rate) parameters.
Many different effects can be set up by varying the forward
binding rate, kd, and the buffer concentration.Calcium pumps
There are two types of calcium pump. A high-affinity, low
volume "pump" ("Ca-ATPase") transports calcium from the cell.
It saturates at high [Ca]i, at a level set by Km, but below this
level, the pump rate is proportional to [Ca] at the calcium shell
just below the surface.
Ica = Vmax * ([Ca]-[CaB]) / ( Km + ([Ca]-CaB] )
Where:
Ica = calcium current from this pump (outward).
[Ca] = calcium concentration at inner surface of membrane.
[CaB]= basal level of calcium below which it is not pumped = tcai.
Vmax = Maximum rate of calcium current (density: mA/cm2).
km = concentration for 1/2 max rate.
The pump's calcium current is added to the total current
in the voltage compartment and also to the total calcium
flux in the calcium compartment. The parameter "dicafrac"
sets the fraction of Ica (default=1) that is added to the current.
Seting this parameter to 0 allows you to set the calcium pump's
rate of calcium flux without affecting current flow.
tempcel=35; /* pump is temperature-dependent */
ddca = 1e-12; /* set to low value to eliminate diffusion */
catau = 50e-3; /* Sets Ca decay tau (used here only) */
at 1 sphere dia 10;
at 1 chan Ca density 1e-5
capump vmax=5e-7/catau km=5e-6 /* gives 50 msec tau @ 35 deg C */
cshell 1;
A second type of calcium pump is the "exchanger". It is a
low-affinity, high-volume calcium transporter that exchanges
Na ions for Ca ions. Its currents are:
Ica = Kex * [ Cao * Nai * Nai * Nai exp (EG * V * F/RT) -
Cai * Nao * Nao * Nao exp ((EG-1) * V * F/RT) ]
Ina = -r * Ica / 2
Where:
Ica = calcium current from this exchanger (outward).
Ina = sodium current from this exchanger (inward).
Cao = external calcium concentration.
Cai = calcium concentration at inner surface of membrane.
Nao = external sodium concentration.
Nai = internal sodium concentration.
Kex = defines rate of calcium current (density: A/mM4/cm2).
EG = partition parameter representing position of V sensor (0.38).
r = exchange ratio (3 Na+ per Ca++)
The exchanger's calcium and sodium currents are added to the
total current in the voltage compartment. The calcium current is
added to the total calcium flux in the calcium compartment.
The parameter "dicaexchfrac" sets the fraction of the calcium
exchanger's current that is added to the total current. Setting
this parameter to zero allows setting the calcium flux rate
without affecting the current flow.
at 1 sphere dia 10;
at 1 chan Ca density 1e-5
capump vmax=1e-5 km=5e-6
caex kex=5e-9
cshell 1;
Click here to return to Channel statement index
Calcium induced calcium release (CICR)
An internal Calcium store using a ryanodine receptor can release
calcium when triggered by a rise in calcium.
casStart /* init ryanodine [Ca] store = 1.6e-6 M */
kfCICR /* passive leak rate const from ryanodine store, 1/s (Goldbeter 1990) */
vm2CICR /* max rate of Ca pump into ryanodine store, 65e-6/ms (Goldbeter 1990) */
vm3CICR /* max rate of Ca pump from ryanodine store,500e-6/ms (Goldbeter 1990) */
k2CICR /* assoc thresh pump const, ryan store uptake,1e-6 M (Goldbeter 1990) */
krCICR /* assoc thresh pump const, ryan store release,2e-6 M (Goldbeter 1990) */
kaCICR /* assoc thresh pump const, ryan store release,0.9e-6 M (Goldbeter 1990) */
nCICR /* Hill coeff, coop pump binding ryan store uptake, 1 (Goldbeter 1990 */
mCICR /* Hill coeff, coop pump binding ryan store release, 1 (Goldbeter 1990 */
pCICR /* Hill coeff, coop pump binding ryan store release, 4 (Goldbeter 1990 */
cas2Start /* init IP3 [calcium] store = 1.6e-6 M */
ip3iStart /* init [IP3] intracellular = 0.4e-6 M */
betaIP3 /* init fractional rate of constant IP3 store release, default 0.31 */
v1IP3 /* init constant IP3 store flux to 7.3e-6/ms (Goldbeter 1990) */
Click here to return to Channel statement index
Calcium binding to inhibit channel
go = gc * ( 1 - Ca^n) / ( Ca^n + kd^n)
Where:
go = output conductance limited by Ca binding
gc = channel conductance without Ca binding
kd = Kd for Ca binding "cakd"
n = Hill Coeff for Ca binding "cahc"
Ca = [Ca]i, internal Ca concentration
kd^n = kd to the n power
Ca^n = [Ca]i to the n power
The cooperativity of the binding is first-order by default but
it can be set with the "cahc" parameter (default dcahc=1). This
works for the "syn2" and "cGMP type 1" channels, and is a very
simple implementation that does not give correct channel noise
properties. The "cGMP type 2" channel is a Markov implementation
that gives more accurate noise properties (see "chancgmp.cc"). Current through Ca channels
The current through a Ca channel can be highly nonlinear
because the internal Ca concentration is very low and thus
internal Ca does not pass through the channel easily to the
outside. This effect is simulated in NeuronC with an
approximation of the "GHK current equation" which gives the
current as a function of the voltage and channel permeability:
if((cratio=(cai + dpki) / cao) < 1.0) {
if (abs(vm) > 1e-5) {
vfact = exp(vm* 2F/R/T);
df = -vm * (1.0-cratio*vfact) / (1.0 - vfact);
}
else df = r2ft * (1-cratio);
}
else df = capnt->vrev - vm; /* driving force */
Where:
df = driving force for calculating current
vm = membrane voltage
cai = internal Ca
cao = external Ca
dpki = internal K
Click here to return to Channel statement index
Setting Nernst and GHK reversal
potentials
The "vrev" parameter defines the reversal potential for a
channel's driving force (voltage). You can set "vrev" for any
channel arbitrarily to cause the channel to be depolarizing or
hyperpolarizing. However it is convenient to have default
values for channels so they automatically work in the way one
would expect in a physiology experiment. One way to do this is to
calculate reversal potentials from the major ions (Na+, K+, Cl-,
Ca++), so that each channel is defined to use one ion and its
reversal potential is set from the ion's Nernst potential.
dpkna = 0; ( sets K permeability in Na chans to 0 )
dpcana = 0; ( sets Ca permeability in Na chans to 0 )
dpnak = 0; ( sets Na permeability in K chans to 0 )
dpcak = 0; ( sets Ca permeability in K chans to 0 )
dpnaca = 0; ( sets Na permeability in Ca chans to 0 )
dpkca = 0; ( sets K permeability in Ca chans to 0 )
dpcaampa= 0; ( sets Ca permeability in AMPA chans to 0 )
dpcacgmp= 0; ( sets Ca permeability in cGMP chans to 0 )
dpcanmda= 0; ( sets Ca permeability in NMDA chans to 0 )
dpcasyn2= 0; ( sets Ca permeability in syn2 chans to 0 )
If you want to keep the Nernst potentials constant without being
redefined automatically with temperature, you can set:
calcnernst = 0; ( do not recalculate Nernst potentials )
( after set by user )
The reversal potential issue is especially important for Ca
channels because internal [Ca] is normally so low that even a
slight permeability to [K] ions is a large factor in the Ca
channel's reversal potential (see "Current through Ca channels"
above).
chan Ca ... vrev=0.05 (sets cai, controls caflux and Ica)
chan Ca ... cai=100e-9 (sets vrev, controls caflux and Ica)
chan Ca ... vrev=0.05 cai=100e-9 (vrev sets Ica, cai controls caflux)
Click here to return to Channel statement index
Strategy for computing reversal and Nernst
potentials.
In order to simulate the effect of temperature and nonselective
permeabilities on the reversal potential for a channel (e.g. the
effect of internal K+ ions on a Ca channel reversal potential),
every channel type contains information about relative
permeability to the major ions, and the simulation keeps track of
the concentration of internal and external ions. Of course only
Ca concentration varies during a simulation (at least for now).
This allows the "correct" reversal potential to be computed for
all Na, K, and Ca channels when there is a minor fraction of the
current carried by another ion.
dpkna relative permeability for K in Na channels 0.08, Hille (1992)
dpcana relative permeability for Ca in Na channels 0.01, Baker et al, (1971), Meves and Vogel, (1973)
dpnak relative permeability for Na in K channels 0.01, Hille (1992)
dpcak relative permeability for Ca in K channels 0.0001,Hille (1992)
dpnaca relative permeability for Na in Ca channels 0.001, Hille (1992)
dpkca relative permeability for K in Ca channels 0.0003,Hille (1992)
dpcaampa relative permeability for Ca in AMPA channels 0.1
dpcacgmp relative permeability for Ca in cGMP channels 0.1
dpcanmda relative permeability for Ca in NMDA channels 0.1
dpcasyn2 relative permeability for Ca in syn2 channels 0.1
Click here to return to Channel statement index
Use of the GHK current equation for channel currents
vna for all Na channels (default +65 mV)
vk for all K channels (default -89 mV)
vcl for all chloride, GABA, and glycine channels (default -70 mV)
As described above, when you change the global variables vna, vk,
or vcl from their default values (with default calcnernst=0) this
causes the corresponding internal ions concentrations to be
recalculated. These new values for ion concentrations will
affect all of the channels that have permeabilities for these
ions.
If you set vna, vk, or vcl variables at the beginning of your
program, their values will be used to generate the reversal
potentials for all of the channel types that are programmed to
use these global variables. If you set "use_ghki = 1", then the
current for each channel type will be determined by the GHK
current equation using the relevant ions and permeabilities for
each channel.
Slope conductance
When you set "use_ghki=1", the simulator uses the GHK current
equation instead of Ohms law to calculate the channel current.
This channel current is a complicated nonlinear function of
voltage, so to compute it for every time step, and for the
iterations within each time step would slow the computation of
each compartment's currents and voltages. Thereore, at run time,
the conductances of the channels are computed with a "slope
conductance" and a "slope reversal potential". These variables
represent a linear approximation of the nonlinear channel
conductance. They are computed for each voltage before run time
and placed into tables for each channel type, indexed by voltage.
Then, at run time, the values are looked up and linearly
interpolated. See the derivation of the slope conductance in the
GHK current equation.
Non-selective channels
Reversal potential for individual channels
Voltage offset of channel gating from external calcium
When external [Ca] is increased, the effective voltage that
many membrane voltage-gated channels sense is hyperpolarized,
e.g. Na conductance is less (Frankenhaeuser and Hodgkin, 1957),
and reversal potentials are slightly depolarized (see below).
Changing the value of "dcao" or "dcoo" (external cobalt) causes a
change in effective voltage offset, which is approximately 18 mV
per factor of 10 change in the concentration of divalent cations.
The amount of change is set by 2 parameters: "dcavoff" sets how
many mV per factor of 10 increase, and the "qcao" field in the
chanparm structure for each channel parameter sets the "base cao"
(i.e. the [Ca] for zero offset) for the voffset calculation.
This automatic feature allows the comparison of voltage gating
data collected at different levels of [Ca]o in the medium.
dcavoff = 0; ( External Ca does not produce voltage offset )
chan Ca ... cao=0.004 ( Set external Ca for local Ca compartment )
The effect of an increase in external divalent cations on the
reversal potential of channels is less than on gating but is
positive, and is set by the "dcaspvrev" variable (default = 0.18),
which multiplies dcavoff (0.018) for a value of 3.2 mV positive
shift in a channel's reversal potential for each factor of 10
increase in cao. See "Reversal potentials, Nernst and GHK
equation" in section 1 of the manual.
dcavoff = 0; ( External Ca does not produce voltage offset )
dcaspvrev = 0; ( Voltage offset does not affect reversal potential )
chan Ca ... cao=0.004 ( Set external Ca for local Ca compartment )
Click here to return to Channel statement index
Markov channel noise
Channel noise is implemented by adding a "noise signal" to the
channel conductance. The noise signal is activated with the
"chnoise" parameter. When "chnoise" is present, the channel
noise is defined by several parameters, "N", "unit" and several
time constants ("taum, tauh, taun, taua, taub, tauc, taud,
tauf"). Some of these parameters have default values and some of
them parameters are also used without Markov noise (see "Setting
unitary conductance"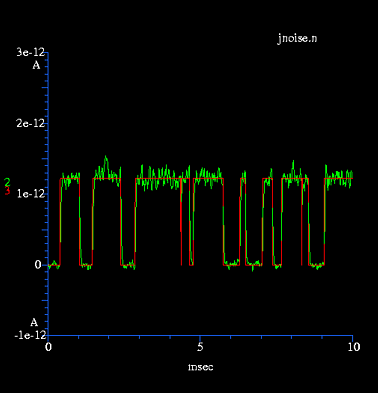
at .... chan .... chnoise=1 [noise parameters]
noise parameters: default
N = <expr> (no default) number of channels for noise
unit = <expr> (set by chan type) size of unitary conductance
rsd = <expr> (set by rseed) random seed for noise
tauc = <expr> 1.0 rate divider for Mg noise
tauf = <expr> 1.0 rate divider for noise flicker
The "unit" parameter describes the unitary conductance of a
single channel and allows the simulator to calculate the number
of channels from the maximum total conductance "maxcond". When N
is set to zero, channel noise is turned off. If you specify a
value for "N", the value of "unit" is ignored:
maxcond = you specify
N = you specify
unit is calculated as = maxcond / N
Otherwise, if you specify both "maxcond" and "unit", the total
number of channels is calculated as:
maxcond = you specify
unit = you specify
N is calculated as = maxcond / unit
If you don't define "N" or "unit", but do specify "chnoise",
the value of N will be computed from either the value of
"maxcond" specified or its default value, and the unitary
conductance will also come from its default:
channel conductance = maxcond or its default
unit = you define or default for channel type
N is calculated as = maxcond / unit
Defaults for "unit" (the unitary conductance) are:
dnau = 12e-12 @22 default Na unitary cond, gives 32 pS @ 33 deg (Lipton & Tauck, 1987)
dku = 11.5e-12 @22 default K unitary cond, gives 15 pS @ 30 deg
dkau = 22e-12 @22 default KA unitary conductance, gives 30 ps @30 deg
dkcabu= 74.3e-12 @22 default BKCa unitary cond, gives 115 pS @ 35 deg
dkcasu= 14.2e-12 @22 default SKCa unitary cond, gives 22 pS @ 35 deg
dampau = 25e-12 @22 default AMPA unitary conductance
dachu = 80e-12 @22 default ACH unitary conductance
dcgmpu = 25e-12 @22 default cGMP unitary conductance
dscu = 25e-12 @22 default 2-state synaptic channel
Note that the default unitary conductances have a temperature
coefficient, set by the Q10 for channel conductance "dqc"
(default = 1.4). The base temperature at which the unitary
conductance is defined is set by the "qt" field of the channel
constants. For membrane channels, the base temperature is
normally 22 deg C, and for synapses it is also 22 deg C. For
more details, look in "Adding New Channels".
var default meaning
------------------------------------------------------------------------------
dbasetc 22 deg C base temp for membrane channel kinetics, conductances
dbasetsyn 22 deg C base temp for synaptic kinetics
dbasetca 22 deg C base temp for ca pumps
dbasetdc 22 deg C base temp for Ca diffusion constant
Click here to return to Channel statement index
Two-state channels
Quantal conductance for HH type channels is calculated with the
following equations that define a 2-state Markov channel (see
"Adding New Channels"):
pa = conduct / tau; /* tau for close -> open */
pb = (1.0-conduct) / tau; /* tau for open -> close */
nco = bnldev(pa,nc); /* delta closed to open */
noc = bnldev(pb,no); /* delta open to closed */
no += nco - noc;
conduct = no / nchan;
where:
pa = probability of opening
pb = probability of closing
tau = average frequency of channel opening
no = number of open channels
nco = number of channels opened per time step
noc = number of channels closed per time step
nchan = number of channels
bnldev = random binomial distribution funtion
conduct = channel conductance
Click here to return to Channel statement index
Multi-state channels
Channel noise for Markov sequential-state channels (e.g. Na
type 1) is implemented by running the sequential-state machine
in "noise mode" where a state describes an integer number of
channels. This defines the kinetics of channel opening and
closing, so no "dur" parameter is needed (and is ignored if
specified). The number of channels "N" and the unitary
conductance "unit" can be specified or can be calculated from
the other parameters (see above), or a standard default unitary
conductance will be used. Recording conductance and state concentration
Using the "G", "G(1)-G(12)" expressions, the channel
internal states may be recorded (see "plot" below). The
expression "G(0) <expr> records the channel conductance in a
manner similar to the "FCx" expression (calib. in S). For a
"sequential-state" type of channel (type 1), the "G(x)" (x=1-12)
expression records the channel state concentrations,
(dimensionless fractions of 1).
G channel conductance (Same as G(0) or G0)
G(I) ionic current through channel
G(vrev) vrev (reversal potential, from GHK V eqn. and permeabilities)
G(Ca) Calcium current through channel (if Ca, NMDA, cGMP chan)
For HH channel types:
G(M) m (if Na chan) or n (if K chan), or c (if Ca chan), frac of 1.
G(H) h (if inactivating type)
For sequential-state Markov types:
G channel conductance (Siemens)
G(0) channel conductance (Siemens)
G(1) amplitude of state 1 (Fraction of 1, or population if "chnoise")
G(2) amplitude of state 2
.
.
.
G(n) amplitude of state n.
Note that the number inside the parentheses is a numerical
expression and can be a variable or a function.
At a node with a calcium channel:
Ca cai = [Ca] at first Ca shell, same as Ca(1)
Ca (0) cao = [Ca] at first exterior Ca shell (next to membrane)
Ca (1) cai = [Ca] at first interior Ca shell (next to membrane)
Ca (2) [Ca] at second shell
.
.
.
Ca (n) [Ca] at nth interior shell
Ca (100) [Ca] in inner core
Ca (-1) same as Ca[0], = [Ca] at first exterior Ca shell (next to membrane)
Ca (-2) cao = [Ca] at second exterior shell
.
.
.
Ca (-n) [Ca] at nth exterior shell
Ca (-100) [Ca] at exterior core
Ca (vrev) local reversal potential for Ca (Nernst potential)
Ca (I) total Ca current through Ca channels and pumps
Ca (IP) Ca current through pump
Ca (IE) Ca current through exchanger
Ca (IPE) Ca current through Ca pump and exchanger
[ Note that exchanger current Ca(IE) includes Ca and Na
currents, and that it is dependent on Vrev of Ca and Na.]
G(0) channel conductance
G(1) population of state 1
G(2) population of state 2
G(3) integration state
G(4) state switching
Click here to return to Channel statement index
Setting the rate functions
If you need to modify the behavior of a channel, remember
that you can use the standard channel types and modify their
behavior by changing the effective voltage (e.g. voffsetm,
voffseth) and/or rate (e.g. taum, tauh). Often this provides
enough flexibility to change the behavior of a channel to make it
work the way you need. Definition of alpha and beta for the "m"
parameter
(interpreted:)
func calcna1m (v, func)
/* Calculate Na rate functions given voltage in mv.
All rates are calculated exactly as in HH (1952) paper.
Original rates were 1/msec, we multiply by 1000 here (MSSEC)
to convert to 1/sec.
The "func" parameter defines:
1 alpha m
2 beta m */
{
local val,x,y;
if (func==1) { /* alpha m */
y = -0.1 * (v+40.);
x = exp (y) - 1.;
if (abs(x) > 1e-5) /* singularity at v = -40 mv */
val = y / x * MSSEC
else
val = 1.0 * MSSEC;
}
else if (func==2) { /* beta m */
val = MSSEC * 4 * exp ((v+65) / -18.);
};
return val;
};
------------------------------------------------------------------------
(compiled:)
double calcna1m (v, func)
/* Calculate Na rate functions given voltage in mv.
All rates are calculated exactly as in HH (1952) paper.
Original rates were 1/msec, we multiply by 1000 here (MSSEC)
to convert to 1/sec.
The "func" parameter defines:
1 alpha m
2 beta m */
{
double val,x,y;
if (func==1) { /* alpha m */
y = -0.1 * (v+40.);
x = exp (y) - 1.;
if (abs(x) > 1e-5) /* singularity at v = -40 mv */
val = y / x * MSSEC
else
val = 1.0 * MSSEC;
}
else if (func==2) { /* beta m */
val = MSSEC * 4 * exp ((v+65) / -18.);
}
return val;
}
/* call before channel is defined or run: */
set_chancalc(NA,1,0,calcna1m); /* sets the 0 (m) param for Na type 1 */
At the beginning of each simulation run, this subroutine is
used to calculate alpha for "m" to make the lookup table used by
the channels during the run. The name used to define the function
is set in the "mak???()" procedure that defines each channel
type. For more details on adding new channels, see Section 6,
"Adding new channels". Adding new channel types
New channel types can easily be added to NeuronC by specifying
additional transition tables and rate functions. These must be
programmed in "C" and are located in separate files (e.g.
"channa1.cc", "channa2.cc", etc). See Section 6, "Adding New
Channels".Channel condensation
After compartments are condensed (see "Compartment condensation
above in "Cable"), the membrane channels in a compartment are
condensed. The reason is to give an advantage in CPU speed by
eliminating unnecessary "data structures" in the simulation.
When channel noise is defined, a channel can represent an
arbitrary number ("N") of unitary conductances at the same point
in a neuron, since they all receive the same voltage stimulus at
the compartment where they are defined. Multiple channels of an
identical type are formed when channels are placed in
compartments that eventually get condensed with their neighbors.
By condensing the channels, one channel structure can represent
all the unitary conductances of the same type at the
compartment.Load
at <node> load <expr> [vrev <expr>
This defines a load resistor in series with a battery which
connects to the membrane leakage at a node. Calibrated in ohms.
Can be used to simulate a synapse, photoreceptor, or membrane
channel.
Resistor
conn <node> to <node> resistor <expr>
This defines a series resistor between two nodes which acts
exactly like a gap junction. Calibrated in ohms.
Gndcap
at <node> gndcap <expr>
This defines a capacitor which adds to the membrane
capacitance in a node's compartment. Calibrated in farads.
Cap
conn <node> to <node> cap <expr>
This defines a capacitor which connects two compartmemnts.
The addition of this element makes the model unstable and it
must be run slowly with the "implicit" mode turned on for
stability. Calibrated in farads.
Batt
conn <node> to <node> batt <expr>
This defines a battery connected between two compartments.
The addition of this element makes the model slightly unstable
and it must be run with "implicit" mode turned on for
stability. Calibrated in volts.
Gndbatt
at <node> gndbatt <expr>
This defines a battery connected between a node and ground.
Calibrated in volts.
External compartments
You can model external current flow and voltages using external
compartments. To model ephaptic effects, you can arrange
Resistors and Gndcaps to simulate current flows in external
space. In this way, a gap junction or pannexin can be connected
from the inside of a cell to an external compartment. Then you
can arrange voltage-gated membrane channels to sense the sum of
the membrane voltage and the external voltage. A membrane
channel senses the result of a positive shift in the external
voltage as an increase in polarization, so the channel senses
hyperpolarization. This will deactivate Na and Ca channels that
are activated by depolarization.
comp *extern_comp;
extern_comp = nd(x,y)->compnt;
predur = 0.01;
step(predur);
addchan_extern (extern_comp, chan);
addchan_extern_ca (extern_comp, chan);
Where:
extern_comp = pointer to the external compartment,
often a node's compartment pointer.
chan = pointer to the channel.
Another effect of external voltages is capacitive coupling via
the membrane capacitance. A positive shift of the external
voltage will depolarize the local cytoplasm of the cell, but this
alone will not activate or deactivate membrane channels, because
the voltage gradient across the membrane does not change.
However, if the positive shift is applied to only one region
of a cell, other regions will receive the internal depoarization
from that one region, allowing membrane channels to be
depolarized by internal current flows within the cell.
comp *extern_comp;
comp *intern_comp;
extern_comp = nd(a,b)->compnt;
intern_comp = nd(c,d)->compnt;
addcomp_extern (extern_comp, intern_comp);
Where:
extern_comp = pointer to the external compartment,
intern_comp = pointer to the internal compartment,
Note that compartments that represent the middle portion of a
cable element, i.e. are not linked to nodes at the cable's ends,
can be accessed using a "for" loop:
for (pnt=compnt; pnt; pnt=pnt->next) {
if (ndn(c,d)->compnt == pnt) {
this is one end.
}
if (ndn(e,f)->compnt == pnt) {
this is the other end.
}
}
Statements for describing stimulus, electrode, recording, and
running
These statements are used to complete the description of
an experiment after a neural circuit is defined. They may
all be included in programs as any other NeuronC statement,
but they do not start with the node connection as do the
neural element statments.
stimulus light, voltage or current clamp stimulus
electrode make an elecrode with series resistance
plot make continuous plot of a node during run
graph graph any variables at end of step or run
display display the neural circuit on screen
step run for short time and stop to allow graphing
run run simulation continuously for high speed
Expressions that "record" values:
V, I, L return voltage (current,light) at a node
FA0-4, FA8, FA9,
FB0-4, FC0-4, FC9 return synaptic neurotransmitter from filter stage
G0-8 return channel conductance or state concentration
Electrode
To make an electrode, you can use the "electrode" statement. It is
similar to the "resistor" statement, except that at the first node,
it contains a small "gndcap" (capacitor to ground) that simulates
the electrode's leakage capacitance. The capacitor is placed
at the first node (i.e. 1 in the example below).
(interpreted:)
conn [1] to [2] electrode rs=10e7 cap=1e-12;
(compiled:)
make_electrode (nd(1),nd(2), rs=10e6, cap=1e-12);
To define the electrode shape:
conn [1] to [2] electrode rs=10e7 cap=1e-12 dia=5 length=100;
noise parameters: default
rs = <expr> (10e6 Ohms, set by "drs") series resistance
cap = <expr> (1e-12 F, set by "deleccap") electrode parallel capacitance
vrest = <expr> (0 mV) starting voltage
dia = <expr> (set by rseed) diameter for display
length = <expr> (set by rseed) length for display
Then, later in the script you can display it:
display electrode matching [1][-1] color 5 dscale 1;
You can also change what your "electrode" looks like by
redefining its icon.
Stimulus
Point stimuli
(interpreted:)
stim node <node> vclamp=<expr> start=<expr> dur=<expr>
stim node <node> cclamp=<expr> start=<expr> dur=<expr>
stim node <node> puff <ligand>=<expr> start=<expr> dur=<expr>
(compiled:)
vclamp (nd(<node>), inten, start, dur);
cclamp (nd(<node>), inten, start, dur);
puff (nd(<node>), ligand, inten, start, dur);
where:
unit:
vclamp =<expr> (volts) set voltage for clamp
cclamp =<expr> (amperes) set current for clamp
start =<expr> (sec) time to start stimulus
dur =<expr> (sec) duration of stimulus after start
puff <nt> =<expr> (M) puff ligand
Ligands available for "puff
Optical stimuli
The "stim node" statements define node stimuli. To
stimulate a single node, a voltage or current clamp may be
used, in which case the node current or voltage,
respectively may be be plotted. An I/V measurement can be
performed by placing a "stim node" statement inside a "for"
loop. These statements are not interpreted by the program
"stim" (see below).
(interpreted:)
stim cone <node> inten=<expr> start=<expr> dur=<expr>
stim rod <node> inten=<expr> start=<expr> dur=<expr>
(compiled:)
stim_cone (nd(<node>), inten, start, dur, wavel);
stim_rod (nd(<node>), inten, start, dur, wavel);
where:
inten =<expr> Q/um2/sec intensity of stimulus
start =<expr> sec time to start stimulus
dur =<expr> sec duration of stimulus after start
wavel =<expr> nm wavelength (also, sun, tungsten or xenon)
The "stim cone" and "stim rod" statements allow
single photoreceptors to be given a point-source light
stimulus. These statements are not interpreted by the
"stim" program (see below). See below for explanation of
parameters.
(interpreted:)
stim spot <expr> loc (<expr>,<expr>) blur=<expr>
inten=<expr> start=<expr> dur=<expr>
mask=<expr>
stim bar <expr> loc (<expr>) blur <expr> inten=<expr>
start=<expr> dur=<expr> mask=<expr>
orient=<expr>
stim sine <expr> loc (<expr>,<expr>) blur=<expr>
inten=<expr> start=<expr> dur=<expr>
sphase=<expr> orient=<expr> tfreq=<expr>
drift=<expr> contrast=<expr>
xenv=<expr> yenv=<expr> mask=<expr>
stim gabor <expr> loc (<expr>,<expr>) blur=<expr>
inten=<expr> start=<expr> dur=<expr>
sphase=<expr> orient=<expr> tfreq=<expr>
drift=<expr> contrast=<expr>
xenv=<expr> yenv=<expr> mask=<expr>
stim sineann <expr> loc (<expr>,<expr>) blur=<expr>
inten=<expr> start=<expr> dur=<expr>
sphase=<expr> orient=<expr> tfreq=<expr>
drift=<expr> contrast=<expr>
renv=<expr> mask=<expr>
stim windmill <expr> loc (<expr>,<expr>) blur=<expr>
inten=<expr> start=<expr> dur=<expr>
sphase=<expr> orient=<expr> tfreq=<expr>
drift=<expr> contrast=<expr>
xenv=<expr> mask=<expr>
stim checkerboard <expr> loc (<expr>,<expr>) blur=<expr>
xenv=<expr> yenv=<expr>
inten=<expr> start=<expr> dur=<expr>
orient=<expr> tfreq=<expr> contrast=<expr>
stim simage <filename> loc (<expr> <expr>); blur <expr>
inten=<expr> start=<expr> dur=<expr>
orient=<expr> xenv=<expr> yenv=<expr>
mask=<expr>
stim sector <expr> inten=<expr> orient=<expr>
start=<expr> dur=<expr>
stim file <filename>
stim backgr <expr>
stim center (<expr>,<expr>)
(compiled:)
stim_spot (double dia, double xloc, double yloc, double inten, double start, double dur);
stim_spot (double dia, double xloc, double yloc, double inten,
double start, double dur, double wavel, double gwidth, double mask);
void stim_spot (double dia, double xloc, double yloc, double inten, double start, double dur,
double mask, int stimchan);
stim_ispot (double dia, double xloc, double yloc, double inten,
double start, double dur, double wavel, double mask, int invert);
stim_annulus (double idia, double odia, double xloc, double yloc,
double inten, double start, double dur);
stim_bar (double width, double height, double xloc, double yloc, double orient,
double inten, double start, double dur, double wavel, double mask, int stimchan);
stim_bar (double width, double height, double xloc, double yloc, double orient,
double inten, double start, double dur, double mask);
stim_bar (double width, double height, double xloc, double yloc, double orient,
double inten, double start, double dur);
stim_grating (int type, double speriod, double sphase, double orient,
double xloc, double yloc, double tfreq, double drift,
double inten, double contrast, double wavel,
double xenv, double yenv, double mask,
double start, double dur);
stim_sine(double speriod, double sphase, double orient,
double xloc, double yloc, double xcent, double ycent,
double tfreq, int drift, double scale,
double inten_add, double inten_mult, double contrast,
int sq, double start, double dur, double wavel, double mask)
stim_sine(double speriod, double sphase, double orient, double
xloc, double yloc, double tfreq, int drift,
double inten, double contrast, double start, double dur);
stim_gabor(double speriod, double sphase, double orient,
double xloc, double yloc, double xcent, double ycent,
double tfreq, double drift, double scale,
double inten_add, double inten_mult, double contrast, double xenv, double yenv,
int sq, double start, double dur, double wavel, double mask);
stim_gabor(double speriod, double sphase, double orient, double xloc, double yloc,
double tfreq, double drift, double inten, double contrast,
double xenv, double yenv, double start, double dur);
stim_sineann(double speriod, double sphase, double xloc, double yloc,
double xcent, double ycent, double tfreq, double drift, double scale,
double inten_add, double inten_mult, double contrast, double renv, double makenv, int sq,
double start, double dur, double wavel, double mask);
stim_sineann(double speriod, double sphase, double xloc, double yloc,
double tfreq, double drift, double inten, double contrast,
double xenv, double start, double dur);
stim_windmill(double speriod, double sphase, double xloc, double yloc,
double xcent, double ycent, double tfreq, double drift,
double scale, double inten_add, double inten_mult, double contrast,
double renv, int sq, double start, double dur,
double wavel, double mask);
stim_windmill(double speriod, double sphase, double xloc, double yloc,
double tfreq, double drift, double inten, double contrast,
double xenv, double start, double dur);
void stim_checkerboard(double width, double height, int xn, int yn,
double orient, double xloc, double yloc,
double xcent, double ycent, double scale,
double tfreq, double inten, double contrast,
double start, double dur, double **stim_rndarr, int *stim_nfr)
void sector_mask(double orient, double width, double val, double stimtime, double dur);
See definitions of these functions in "ncstimfuncs.cc" and "ncfuncs.h".
where:
units:
spot <expr> um diameter of spot
bar <expr> um width of bar
sine <expr> um spatial period of sine wave grating
gabor <expr> um spatial period of gabor wave grating
sineann <expr> um spatial period of sine wave grating
windmill <expr> um number of vanes of sine wave windmill
simage <expr> image file
loc (<expr>,<expr>) spatial location (x,y) or (xmin,xmax) for stimulus
sscale = <expr> default=1 resolution of blur convolution
inten = <expr> Q/um2/sec intensity of stimulus
inten_add = <expr> Q/um2/sec mean intensity of grating (sine,gabor,sineann,windmill)
inten_mult= <expr> Q/um2/sec contrast scaling for of grating (sine,gabor,sineann,windmill)
start = <expr> sec time to start stimulus
dur = <expr> sec duration of stimulus after start
backgr = <expr> Q/um2/sec intensity of background
wavel = <expr> nm wavelength (also, sun, tungsten, xenon, or led)
gwidth = <expr> nm Gaussian width (1/e of max) for LED stimuli, default 0 => monochromatic.
contrast = <expr> (L1-L2)/(L1+L2) fractional contrast of grating
tfreq = <expr> Hz (cy/sec) Temporal frequency
drift = <expr> 0 = 1 -> Drifting grating
sphase = <expr> deg [optional] Spatial phase (offset) for grating
orient = <expr> deg [optional] Orientation from vertical
xenv = <expr> um [optional] Radius of X Gaussian envelope (def=50um), (or grating size, def=inf)
yenv = <expr> um [optional] Radius of Y Gaussian envelope (def=50um), (or grating size, def=inf)
blur = <expr> um [optional] dia (at 1/e) of Gaussian blur func.
mask = <expr> na [optional] masking: 0->transparent, 1->masking
stimchan = <expr> na [optional] stimulus channel: 0->default, 1-9 independent masking
scatter = <expr>,<expr> um [optional] dia (at 1/e) of Gaussian blur func.
sq = <expr> for sine stimuli, sq=1 -> square wave, sq=0 -> sine wave
pie_mask = 2 partly overlapping bar masks that together produce a pie-shaped stimulus
Optical blur and scatter
For more realism, the "stim" program can generate stimuli
with optical blur and light scatter (see "Running "stim").
"Stim" operates only on the stimulus and photoreceptor
statements, and ignores all other neural element statements. The
blur is a Gaussian function, defined by its diameter at 1/e of
peak amplitude. This blur defines a convolution of the stimulus
(from one or more "spot", "bar", or "sine" statements above) with
the appropriate optical blur function. Only one convolution is
performed (i.e. no separate convolution is performed to simulate
the effect of photoreceptor aperture). However the effect of
photoreceptor aperture can be simulated by 1) increasing the size
of the stimulus (i.e. increasing a point-source stimulus into a
spot the size of the photoreceptor aperture) or 2) increasing the
size of the optical blur Gaussian. See the description of "rod"
and "cone" photoreceptors for more details on this process. Optical scatter
The effect of scatter is specified separately from optical blur
because the eye's optics have sources of blur that originate in
at least 2 different mechanisms. The "blur" function (described
above) originates in diffraction so it is smaller with a larger
pupil. The "scatter" function is larger with a larger pupil,
and is generally only a fraction of the amplitude of the "blur"
function. Several types of scatter can be given. To describe
a Gaussian scatter, set its diameter and relative amplitude.
scatter <expr>, <expr>
(amplitude) (diameter)
where:
amplitude = scatter function's amplitude relative to the blur function
diameter = diameter for scatter function
To describe a non-Gaussian scatter function, it can be described
as a radial power function. The value set for its "power"
distinguishes it from a Gaussian:
scatter <expr>, <expr>, <expr>
(amplitude) (diameter) (power)
where:
amplitude = scatter function's amplitude relative to the blur function
diameter = diameter for scatter function
power = power for scatter function
scatter function = 1 / (1 + pow(r/(diameter/2), power))
If "scatter" is given no arguments, the scatter function from
Robson and Enroth-Cugell (1978) is added to the blur function
used by the "stim" program to generate a stimulus. This is
appropriate for the cat eye. The "blur" and "scatter" functions
are added together and the resulting optical blur function is
normalized so its volume is 1. Therefore, if the amplitude of
the "scatter" function is set greater than 1, it predominates
over the "blur" function (see "stimsub.cc"). Some useful blur
and scatter functions are:
blur 22
scatter (.15, 45, 2.5) Robson & Enroth-Cugell (1978), 4 mm pupil, cat
(default)
blur 4.677
scatter (.0427, 20.35) Campbell & Gubisch (1966), 2 mm pupil, human
Gaussian scatter function fit by Geisler (1984)
Blur=4.677 includes 4.43 blur, 1.5 cone aperture.
blur 1.5
scatter (10, 5.4, 1.95) Campbell & Gubisch (1966), 5.7 mm pupil, human
scatter (1000, 2.6, 1.85) Guirao et al, (2001), 5.8 mm pupil,
"best refracted" average human eye
scatter (1000, 3, 1.0) Guirao et al, (2001), 5.8 mm pupil
"uncorrected" average human eye
Stimulus convolution
The stimulus convolution is performed on 2-dimensional arrays
by default at a resolution of 1 micron (see below for finer
resolution). The size of the stimulus convolution array is equal
to the sum of the photoreceptor array size and "blur array" size
(5 x the Gaussian blur diameter). This implies two things: 1)
all stimuli within reach of a photoreceptor will always fall
within the stimulus array, and 2) the stimulus array becomes very
large with large photoreceptor arrays or wide blurs. Although
all the location and size parameters for stimuli can be specified
in "floating point" (i.e. they may have fractional parts) the
convolution is done with location coded as an integer.
Stim file
The computation of a blurred stimulus takes a lot of time,
so normally "stim" is run once on a NeuronC program file and
generates a "stimulus file" which contains stimulus events, one
event per receptor at a certain time. Thus if the same
stimulus and photoreceptor locations are used in many different
NeuronC runs, the stimulus file need only be generated once.
The "stim file" statement defines for "stim" which file to
generate, and the same statement tells NeuronC which file to
read for the stimulus event list. If a "stim file" statement
is defined before other "stim" statements, NeuronC ignores all
other light stimulus statements in a program.
Sine, Gabor, Sineann
The "stim sine", "stim gabor", "stim windmill", and "stim
sineann" statements produce a 2D sine wave grating with the given
spatial period. For the "sine" and "gabor" gratings, if the
"orient" parameter is not set, the grating is oriented vertically
(parallel with the Y-axis). The "sphase" parameter defines the
spatial phase in degrees; if it is not defined it is assumed to
be zero and the center of the sine wave grating starts from the
position defined by the "loc (X,Y)" parameter. To set a central
peak (i.e. a cosine grating), set the "sphase" parameter to 90.
The "tfreq" parameter sets the temporal drift frequency,
calibrated in Hz. If no "drift" parameter is given (or if it is
set to zero), the stimulus is a static grating. The "drift"
parameter sets the grating in motion. Positive values mean drift
left -> right (drift can be set to 1, 0 or -1). Note that for a
constant "tfreq", different drift rates (um/sec) are produced
with different spatial periods. The grating is produced with a
temporal step set by the "dsintres" global variable (default =
0.002 -> 500 steps per cycle). To prevent the time steps from
being set too small they are set to a minimum of "dsintinc"
(default=0.002 sec).
Wavelength
The "wavel" parameter specifies the spectral properties of the
stimulus. A number defines the wavelength of a monochromatic
light stimulus or the center wavelength of a narrow-band LED
stimulus. The "gwidth" parameter describes the Gaussian width
of the spectrum, centered on the value of "wavel". If "gwidth" is
0, the spectrum is monochromatic. It is also possible to give a
"white" stimulus by specifying "sun", "tungsten" or "xenon"
instead of a numerical value for "wavel". Wavelengths are
limited to between 380 and 800 nm. Photoreceptor sensitivities
are calculated from action spectra tables at 5 nm intervals,
quadratically interpolated between points. When a spectrally
extended light source is selected (i.e. sun, tungsten, xenon),
its intensity is normalized using the appropriate scotopic or
photopic luminosity function so that responses may be compared
across photoreceptors and light sources.Center
The "stim center" statement defines for the "stim" program
the location of the center of the array used for calculating
the light distribution. The stimulus array is of a limited size
(512 x 512), so it is sometimes necessary to move the array to
preserve an offset stimulus. Normally the location for the
center is (0,0) which is the default. Background intensity
The "stim backgr" statement defines a background level for
all receptors. This is normally used once for the beginning of
a simulation run, but can be used several times during a run.
A new background value defined by the "backgr" statement
supercedes an old one. The "backgr" statement erases any
stimuli currently in effect, so if you're using another
stimulus and want to simultaneously change the background, use
a very large spot for the background. Masking and transparency
To allow a stimulus to mask other stimuli, include the "mask"
parameter in any stim statement. If "mask" is set to 0, the
stimulus is transparent, and if set to 1, it masks other stimuli.
Between 0 and 1 it is partially transparent. For example, to
place a gray spot in the middle of another stimulus, simply
include a spot statement that includes "mask 1":
(interpreted:)
stim spot 10 loc (25,25) inten=10 mask=1 start=time dur=.02;
(compiled:)
stim_spot (dia=10, 25, 25, inten=10, start=time, dur=0.02, wavel=1, mask=1);
(interpreted:)
// Standard stim and backgr statements...
stim backgr 1000
stim sine ...
// Then, the mask stim and backgr statements...
unmaskthr = -100;
stim backgr 100 mask=1 start=0;
stim spot 10 loc (25,25) inten=-200 mask=1 start=time dur=.02;
step 0.001;
(compiled:)
// Standard stim and backgr statements...
stim_backgr (1000);
stim_sine (...)
// Then, the mask stim and backgr statements...
unmaskthr = -100;
stim_backgr (backgr=100, wavel=1, mask=1, start=0);
stim_spot (dia=10, 25, 25, inten=-200, start=time, dur=0.02, wavel=1, mask=1);
step (0.001);
Mask for voltage stimulus
When using a photorec in a neuron as a voltage clamp, the stimulus will be a
voltage, not an intensity. Since the voltage will normally be negative,
the variable "unmaskthr" will not work correctly, as it sets a negative
masking threshold. To set a positive masking threshold, you can set the
variable "unmaskthr2" to a negative voltage that is more positive than
the voltages in the applied voltage clamp to the photorec.
Similar to the "unmaskthr" example above, except this will mask a
circular spot with a mean "intensity-voltage". It is not necessary
to set a background for the mask:
(interpreted:)
// Standard stim and backgr statements...
stim backgr 1000
stim sine ...
// Then, the mask stim statement...
unmaskthr2 = -0.001;
stim spot 10 loc (25,25) inten= -0.045 mask=1 start=time dur=.02;
step 0.001;
(compiled:)
// Standard stim and backgr statements...
stim_backgr (1000);
stim_sine (...)
// Then, the mask stim statement...
unmaskthr2 = -0.001;
stim_spot (dia=10, 25, 25, inten= -0.045, start=time, dur=0.02, wavel=1, mask=1);
step (0.001);
Sector Mask
The "sector" statement sets up a sector that masks everything but
the sector defined by the first parameter (interpreted) which is the sector
width in degrees and the orientation:
interpreted:
sector 45 orient=90 inten=1000 start=0.1 dur=2.0;
sector 45 orient=90 loc (100,200) inten=1000 start=0.1 dur=2.0;
compiled:
sector_mask(orient, width, inten, stimtime, dur);
sector_mask(orient, width, xloc, yloc, inten, stimtime, dur, stimchan);
The sector function sets up 2 masking bars that are oriented to
unmask the sector defined by the user. The bars are set to be
1000 microns long, so if your photoreceptor array extends beyond
that you should revise the constant BARLENGTH (in ncstimfuncs.cc and
modcode.cc).
Stimulus Channels
To set up several stimuli each with its own mask, you can create
stimuli in "stimulus channels" which are independent stimuli that
are summed by each photoreceptor. For example, to set 2 stimuli
with masks, you set the first with stimchan=0, and the second
with stimchan=1. They are created separately, and only the
appropriate mask is applied to each one. After the stimuli in
each stimulus channel are summed, a mask set for that stimulus
channel will mask the summed stimuli. By default, a photoreceptor
is sensitive to the sum of all the masked stimuli from all the
stimulus channels. Note on where to place "stim" statement:
It is possible to write a "stim" statement that looks
correct but does not generate the stimulus correctly. For
example, if timinc=1e-4 and you give a time step of 0.01111111,
the simulator will run for 0.0112 sec which is .01111111
rounded up to the next larger interval. This is usually not a
problem, but if you place the "step" statement inside a "for"
loop along with "stim" statements, you may find that the
stimuli are not being started at the correct times because of
the "roundoff" problem stated above. The way to correct this
problem is to make 2 separate "for" loops, one to generate the
stimuli, and one to run the "step" statement:
timinc = 0.0001;
steptime = 0.011111111111; /* not integral mult of timinc */
for (i=1; i<n; i++) {
stim .... start=i*steptime dur=steptime; /* correct to 0.0001 sec */
};
for (i=1; i<n; i++) {
plotarr[i] = V[node1];
step steptime; /* step 0.0112, but maybe acceptable */
};
When the "stim" statements are all executed before the
first "step" statement, they are all run in "construction
mode" before the model starts, so they are correctly
synchronized with the integration time step. Another
solution is to use the "time" variable which always has the
correct time updated by the "step" statement:
timinc = 0.0001;
steptime = 0.011111111111; /* not integral mult of timinc */
for (i=1; i<n; i++) {
plotarr[i] = V[node1];
stim .... start=time dur=steptime; /* may give blank betw. stimuli */
step steptime; /* still steps 0.0112 sec */
};
Note on the stimulus time step and resolution
The stimuli are normally run at a time resolution of "stiminc" (default 0.0001
sec), the time step for running synapses, even when the basic timestep for the
simulator "timinc" is smaller. The reason for this is that for a large model
with many photorecptors (or v/itransducers) the list of stimuli can be very
long, and most stimuli don't need to be displayed with higher resolution than
0.1 ms.
Test of accuracy in a continuing sum such as "simtime":
test2.cc:
----------------------------------------
#include <stdio.h>
double val = 0;
double inc = 3e-10;
double n = 1e5;
main(int argc, char **argv)
{
int i;
for (i=0; i<n; i++) {
val += inc;
}
printf ("%7.4g %20.20g\n",n,val);
}
----------------------------------------
nc/src> make test2
g++ -c -g -I../libP -I../pl test2.cc
cc -g test2.o -o test2
(note: have added spaces to align "val":)
n val
----------------------------------------
1e+04 2.9999999999994338345e-06
1e+05 3.0000000000045564356e-05
1e+06 0.00029999999999524000092
1e+07 0.0030000000006714456005
1e+08 0.030000000036306033457
1e+09 0.30000000203657323228
When compiled with n set to different values, the accuracy of the accumulated
val (a double precision value) goes down by a little less than 1 digit per
factor of 10 increase in n. Note on the "stim" program:
The "stim" program ignores the "stim vclamp", "stim cclamp",
"stim rod" and "stim cone" statements, and therefore these
stimuli will not produce an entry in the stimulus file.
Instead these statements are always interpreted by the "nc"
program. This allows running a neural circuit with one
stimulus file but different microscopic stimuli such as voltage
or current clamps, or individual photoreceptors.Plot statement
The plot statement is used to plot a continuous record
from a node, stimulus or variable, and has been optimized to
run very fast. Plotting works only during a "run" statment
(see below) and thus does not work when NeuronC is setting up a
network or after a "run" statement is finished (after "endexp"
time).
(interpreted:)
plot V [<node>]
plot V [<node>], V[<node>] ...
plot V [<node>] max <expr> min <expr>
plot V [<node>] max <expr> min <expr> <options>
plot Vm [<node>] max <expr> min <expr> <options>
plot I [<node>] max <expr> min <expr> <options>
plot L [<node>] max <expr> min <expr> <options>
plot func max <expr> min <expr> <options>
plot S variable max <expr> min <expr> <options>
plot FAn <element> max <expr> min <expr> <options>
plot FBn <element> (same options)
plot FCn <element> (same options)
plot G(n) <element> (same options)
plot Ca(n) [<node>] (same options)
(compiled:)
plot (V, <node>);
plot (V, <node>, max=<expr>, min=<expr>);
plot (VM, <node>);
plot (I, <node>);
plot (L, <node>);
plot (V, <element>);
plot (FAn, n, <elemnum>, max=<expr>, min=<expr>);
plot (FBn, n, <elemnum>, max=<expr>, min=<expr>);
plot (FCn, n, <elemnum>, max=<expr>, min=<expr>);
plot (Ca, n, <elemnum>, max=<expr>, min=<expr>);
plot (G, n, <elemnum>, max=<expr>, min=<expr>);
plot_func (double(*func)(double val, double t), double plval, double max, double min);
plot_var (double *var, double plval, double maxx, double minx);
followed by:
plot_param(name=<string>, plnum=<expr>, plsize=<expr>);
plot_param(name=<string>, pen=<expr>, plnum=<expr>);
plot_param(name=<string>, pen=<expr>, plnum=<expr>, plsize=<expr>);
plot_param(name=<string>, pen=<expr>, plnum=<expr>, plsize=<expr>, plval=<expr>);
You can also follow these by:
void plotchar (int val,int lines, int i); uses char symbol instead of line
void plotvpenc (double (vpen)(int,double,double)); inserts virtual pen in plot
void plotfilt (int nfilt, float *timec); inserts low-pass filter in plot
plot_arr (double *arr, int arrsize); puts xval,yval into array "arr[arrsize][2]"
where: (interpreted or compiled:)
[<node>] = 1-, 2- or 3-D node number; must have brackets.
max <expr> (volts) = maximum voltage for vertical plot axis
min <expr> (volts) = minimum voltage for vertical plot axis
plmin, plmax are default values for max and min
when not specified.
func = a function returing value to plot
variable = any variable
<options> = pen <expr> sets color of single plot.
char 'x' char labels with lines.
Char 'x' char labels without lines.
size <expr> size of char point label.
filt <expr> lowpass filter (tau in sec).
filt [<expr>,<expr>] cascade lowpass filter.
vpen <func> function returning pen color
plname <expr> name for plot
plnum <expr> plot number assignment (if plsep)
plsize <expr> plot size (if plsep)
plval <expr> constant value to pass to func
plarr <expr> puts xval,yval into array "arr[arrsize][2]"
These statements plot the voltage as a function of time
at the nodes specified on a single graph. If "max" and
"min" are left out of the statement, the voltage scale
(ordinate) is defined by the variables "plmax" and "plmin".
These variables are set by default (plmax = 0.04, plmin =
-0.07) to the normal physiological range of neurons, and in
many cases they need not be changed. The variable "endexp"
(length of the experiment) sets the time scale (abscissa),
and the "ploti" variable sets the time resolution of the
plot. The "plot Vm" statement plots the membrane voltage,
that is, the difference between the intracellular voltage
and the extracellular voltage at an external compartment.
plot .... filt [ 3.2e-5, 1.6e-6, .8e-5];
(compiled:)
plotfilt(3,make_filt(3.2e-5, 1.6e-6, .8e-5));
This plot filter would have a cascade of single-pole filters in series with
3dB cutoff frequencies of 5KHz, 10KHz, and 20KHz. The filter is applied to the
previous "plot" statement.
(compiled:)
plotbessfilt(2000); // 4th order bessel filter, cutoff = 2000 Hz
You can define a special "pen" function for each plot using the
"vpen" option. This function receives the plot number and the X
and Y values for the plot, and returns a number which is
interpreted as the "pen" number (0-15 = color, -1 = no display).
The advantage of this method over the "onplot" method defined
below is that if the plot number changes when you add more plots,
the color of the plot is defined by the same function.
(interpreted:)
func spikplot (nplot, xval, yval)
{
local retval;
if (yval > 25) retval = 7 /* white if > 25 */
else retval = 6; /* brown otherwise */
if (yval < 10) retval = -1; /* disappear if less than 10 */
return (retval);
};
After this pen color function is defined, you can call the
function from a "plot" statement:
plot V[100] max 0.01 min -0.07 vpen spikplot; /* set plot time function */
(compiled:)
double spikplot (int nplot, double xval, double yval)
{
double retval;
if (yval > 25) retval = 7 /* white if > 25 */
else retval = 6; /* brown otherwise */
if (yval < 10) retval = -1; /* disappear if less than 10 */
return (retval);
}
plot_vpen (spikplot);
plot (V, nd(100), max=0.01, min=-0.07);
The vpen function is called before the plot variables are
recorded. You can include other actions in it, much like the
"onplot()" procedure.
plot I [<node>] max=<expr> min=<expr> <options>
where:
[<node>] = 1-, 2- or 3-D node number; must have brackets
max=<expr> (amperes) = maximum current for vertical plot axis
min=<expr> (amperes) = minimum current for vertical plot axis
<options> = pen and char statements as in plot above.
This statement plots the current passed through the
electrode of a node which has been voltage clamped. It
works exactly like the "plot V[]" statement in that several
plots of current and/or voltage can be combined on the same
graph with different scales. If a current clamp is
connected to the node, without a voltage clamp, the "plot
I[]" statement plots the current passed through the current
electrode. Note that to record the current at the "end" of a
voltage clamp period, the voltage clamp must still be present.
One way to assure this is to record the current at a small time
step before the voltage clamp stops.
plot L [<node>] max <expr> min <expr>
where:
[<node>] = 1-, 2- or 3-D node; must have brackets
max <expr> (photons/sec) = maximum "inten"
min <expr> (photons/sec) = minimum "inten"
<options> = pen and char statements as in plot above.
This statement plots the light flux (number of photons/sec)
absorbed by a photoreceptor at a node. It is useful for
determining single photon events or plotting the stimulus timing
on the same graph as the voltage or current in a node. "max" and
"min" determine the scale for plotting. Remember, the number of
photons absorbed is related to light intensity, photoreceptor
absorbing area, and absorption factors ("dqeff"=0.67, "attf"=0.9,
and the pigment absorption).
plot <func> max <expr> min <expr>
This statement plots the value returned by a function. The
function must have 2 input parameters: a number set by
"plval=val" (a param on the plot line) or if this has not
been set, the number of the plot, and the X value, and
must return the Y value.
(interpreted:)
dim contrast_array[endexp/ploti+1];
func contrast_val (plval, xval)
/* Return and save the contrast value */
{
contr = (V[1]- V[0]) / (V[1] + V[0]);
contrast_array[xval] = contr;
if (contr >= plval) contr = plval;
return (contr);
};
(compiled:)
double contrast_array[1000];
double contrast_val (double plval, double xval)
/* Return and save the contrast value */
{
contr = (v(nd(1))- v(nd(0))) / (v(nd(1)) + v(nd(0)));
contrast_array[(int)xval] = contr;
if (contr >= plval) contr = plval;
return (contr);
};
plot_func (contrast_val, plval=100, max=<expr>, min=<expr>);
Note that you can accomplish several things in a plot function,
e.g. you can load arrays with recorded values, or modify the
neural circuit. Since it runs once every "ploti" time increment
(which can be much longer than the integration time increment
"timinc") it takes relatively little CPU time.
dim plot_array[501][2];
plot V[1] plarr plot_array;
.
.
.
run;
process data in plot_array here.
(compiled:)
double plot_array[501][2];
plot_arr (plot_array,501); // puts xval,yval into array "arr[arrsize][2]"
plot S variable max <expr> min <expr>
This statement plots the value of any symbol
(variable) together with other plot statements.
(interpreted:)
plot FAx <element expr>
plot FBx <element expr>
plot FCx <element expr>
plot Gy <element expr>
plot FAx <element expr> max=<expr> min=<expr>
plot FBx <element expr> max=<expr> min=<expr>
plot FCx <element expr> max=<expr> min=<expr>
plot G(s) <element expr> max=<expr> min=<expr>
plot G(g) <element expr> max=<expr> min=<expr>
plot G(hh) <element expr> max=<expr> min=<expr>
plot nt [<node>] max=<expr> min=<expr>
plot Ca(z) [<node>] max=<expr> min=<expr>
(compiled:)
plot (FAn, n, <elemnum>, max=<expr>, min=<expr>);
plot (FBn, n, <elemnum>, max=<expr>, min=<expr>);
plot (FCn, n, <elemnum>, max=<expr>, min=<expr>);
plot (G, n, <elemnum>, max=<expr>, min=<expr>);
plot (nt, n, <node>, max=<expr>, min=<expr>);
plot (Ca, n, <node>, max=<expr>, min=<expr>);
where:
x = 0 - 4 = filter number
s = 0 - 12 = state number
g = vrev, I, CA = params for any channel type
hh = H, M = params for HH channels
nt = GLU,AMPA,NMDA,ACH = ligands
CNQX,GABA,BIC,
STR,GLY,STR,
cGMP,cAMP
z = I,IP,IE,IPE,VREV = params at a node with Ca chans
z = 0, 1, 2 ... n = [Ca] in shells, 0=outside, 1=inside, 100=core
and:
<element expr> = number or variable describing a synapse,
from "ename" clause.
max=<expr> = maximum for plot, value depends on filter
min=<expr> = minimum for plot, value depends on filter
This statement plots the neurotransmitter time functions
inside a synapse or channel. The synapse (channel) is
identified using an "ename" in its definition statement,
when it is first made (see "ename" and "modify" below).
Thereafter, the synapse (channel) can be referred to by a
unique value (its element number) retrieved from the
"element".
G channel conductance (Same as G(0) or G0)
G(I) ionic current through channel
G(vrev) vrev (reversal potential)
G(Ca) Calcium current through channel (if Ca, NMDA, cGMP chan)
For HH channel types:
G(M) m (if Na chan) or n (if K chan), or c (if Ca chan), frac of 1.
G(H) h (if inactivating type)
For sequential-state Markov types:
G channel conductance (Siemens)
G(0) channel conductance (Siemens)
G(1) amplitude of state 1 (Fraction of 1, or population if "chnoise")
G(2) amplitude of state 2
.
.
.
G(n) amplitude of state n.
Note that the number inside the parentheses is a numerical
expression and can be a variable or a function.
At a node with a calcium channel:
Ca (0) cao = [Ca] at first exterior Ca shell (next to membrane)
Ca (1) cai = [Ca] at first interior Ca shell (next to membrane)
Ca (2) [Ca] at second interior shell
.
.
.
Ca (n) [Ca] at nth shell
Ca (100) [Ca] in core
Ca (vrev) local reversal potential for Ca
Ca (I) total Ca current through Ca channels and pumps
Ca (IP) Ca current through pump
Ca (IE) Ca current through exchanger
Ca (IPE) Ca current through Ca pump and exchanger
[ Note that exchanger current Ca(IE) includes Ca and Na
currents, and that it is dependent on Vrev of Ca and Na.]
G(0) channel conductance
G(1) population of state 1
G(2) population of state 2
G(3) integration state
G(4) state switching
To look inside a rod or cone transduction element, the
G(0) - G(9) values plot:
G(0) conductance
G(1) rhodopsin
G(2) meta rhodopsin I
G(3) meta rhodopsin II (R*) activates G protein
G(4) G protein
G(5) PDE
G(6) G cyclase
G(7) cGMP
G(8) Ca feedback for recovery and adaptation
G(9) Cax (protein between Ca and G cyclase)
Record and graph
(interpreted:)
V [<node>] voltage at node
V @ cable <element expr> : <expr> voltage along cable
I [<node>] current
L [<node>] light
FAx <element expr> pre-synaptic filters
FBx <element expr> post-release filters
FCx <element expr> post-saturation filters
G(s)
These functions return the values of voltage,
current, or light absorbed, respectively, at any node.
The node may be 1-, 2-, 3-, or 4-dimensional. For instance,
the record function "V[]" can be used to find voltages
at pre- and post-synaptic nodes, and these voltages may
be plotted (see explanation above) or graphed (see
programming example below). The "I[]" statement returns the
currrent injected at a node through a voltage clamp if
present. When a current clamp is present without a voltage clamp
(the ususal case), the "I[]" statement returns the current
clamp's current. Note that to record the current at the "end" of
a voltage clamp period, the voltage clamp must still be present.
One way to assure this is to record the current at a small time
step before the voltage clamp stops.
graph X max=<expr> min=<expr>
graph Y max=<expr> min=<expr> <options>
For setting X and Y scales of graph axes and initial color.
where:
<options> = pen <expr> sets color of single plot.
char 'x' char labels points with lines.
Char 'x' char labels points without lines.
filt <expr> lowpass filter (tau in sec)
filt [<expr>,<expr>] cascade lowpass filter
graph init
For drawing graph axes on screen.
graph restart
For resetting graph so lines don't connect to
previous lines.
graph pen (<expr>, [<expr>] ... )
where <expr> is the number of color (1-16 on VGA and X screen)
For changing pen color of lines on graph between plots,
after the axes have been drawn. The differnt <expr>
numbers are the colors assigned respectively to different plots.
A color of -1 means do not display.
graph (<expr>,<expr>)
where:
(<expr>,<expr>) is an (x,y) point to be graphed.
Draws a new point by connecting it to others with line.
The graph statement allows the display of variables before
or after a "run" or "step" (not while running!). Graphed
points are connected by lines, in a color specified by the
"graph pen" command. Both x and y axes must be initialized
(with "graph X ..." and "graph Y ..." statements) to allow the
graph scale to be set up and the graph axes labeled. The
"graph (x,y)" statement then plots a sequence of points as
connected line segments. The "restart" command allows multiple
sets of points connected by lines to be drawn on the same grid.
Any variable (or node voltage/current/ intensity) may be
plotted. Calibrated in same units used to record.
(interpreted:)
graph X max -.01 min -.08; /* volts */
graph Y max -2e-11 min -6e-11; /* amps */
graph init;
graph pen (4);
for (i=0; i<10; i++) {
stim node 1 vclamp i * -.01 start i * .02 dur .02; /* sweep voltage */
step .02; /* wait for equilbration */
graph (V[1], I[1]); /* graph result */
};
graph restart; /* this time stim node 2 */
graph pen (2,3);
for (i=0; i<10; i++) {
stim node 2 vclamp i * -.01 start i * .02 dur .02; /* sweep voltage */
step .02; /* wait for equilbration */
graph (V[1], I[1]); /* graph result */
};
(compiled:)
graph_x(max= -0.01, min= -0.08); /* volts */
graph_y(max= -2e-11, min= -6e-11); /* amps */
graph_init();
graph_pen (4);
for (i=0; i<10; i++) {
vclamp(nd(1), i*-0.01, start=i*0.02, dur=0.02); /* sweep voltage */
step (0.02); /* wait for equilbration */
graph (v(1), i(1)); /* graph result */
}
graph_restart(); /* this time stim node 2 */
graph_pen (2,3);
for (i=0; i<10; i++) {
vclamp( nd(2), i*-0.01, start=i*0.02, dur=0.02); /* sweep voltage */
step (0.02); /* wait for equilbration */
graph (v(1), i(1)); /* graph result */
}
;
;Separate Plots
nc --plsep 1 file.n
or
nc -S file.n
The "-S" or "--plsep 1" command line switches set the "plsep"
parameter when you call "setvar()" in the script. If you place
"plsep=1" before the "setvar()" statement, then you can turn off
separate plots with "--plsep 0" in the command line. See "Setting
variables from command line".
(interpreted:)
plot V[1] pen 2 plname "V1" plnum 2; /* the first 2 are on the same plot */
plot V[3] pen 3 plnum 2;
plot V[5] pen 5 plname "V5" plnum 10;
plot V[6] pen 6 plname "V6" plnum 11;
(compiled:)
plot (v,ndn(1), max, min); plot_param(name="V1", pen=2, plnum=2); /* the first 2 are on the same plot */
plot (v,ndn(3), max, min); plot_param(name="", pen=3, plnum=2);
plot (v,ndn(5), max, min); plot_param(name="V5", pen=5, plnum=10);
plot (v,ndn(6), max, min); plot_param(name="V6", pen=6, plnum=11);
(interpreted:)
plot V[1] pen 2 plname "V1" plnum 2 plsize 2; /* sets this plot bigger */
plot V[3] pen 3 plnum 2;
plot V[5] pen 5 plname "V5" plnum 10;
plot V[6] pen 6 plname "V6" plnum 11;
(compiled:)
plot (v,ndn(1), max, min); plot_param,name="V1", pen=2, plnum=2, plsize=2); /* sets this plot bigger */
plot (v,ndn(3), max, min); plot_param(name="", pen=3, plnum=2);
plot (v,ndn(5), max, min); plot_param(name="V5", pen=5, plnum=10);
plot (v,ndn(6), max, min); plot_param(name="V6", pen=6, plnum=11);
(interpreted:)
plg = .3e-6;
offtr = .2;
offb = 1e-6;
plot Ca(1)[soma] max (1-offtr)*plg+offb
min (0-offtr)*plg+offb
pen 6 plsize .3 plname "[Ca]i" plnum 1;
(compiled:)
max=(1-offtr)*plg+offb;
min=(0-offtr)*plg+offb;
plot (Ca, ndn(1,soma), max, min); plot_param(name="[Ca]i",pen=6, plnum=1, plsize=0.3);
Plotting into frames
With the use of the "gframe", "gorigin" and "gsize"
statements, it is possible to arrange several graphs on the
screen (or a page on printout). By placing a "gframe"
statement before "graph" or "run" statements, the graphical
output is directed to a subset of the screen (called a "frame")
which may be scaled smaller than, and translated with respect
to, the screen. For more information about these statements,
see "Graphics statements",at the end of this section.
gframe "gr1";
gorigin (0.2,0.2);
gsize (0.5);
code that generates graph or plot in smaller frame
. . .
gframe "..";
code to draw on overall screen
.
.
.
gframe "gr2";
gorigin (0.6,0.2);
gsize (0.4);
code to generate second small graph
gframe "..";
etc.
Display statement
Display
(interpreted:)
display matching <node> 'parameters'
display <elemtype> matching <node> 'parameters'
display range <node> to <node> 'parameters'
display <elemtype> range <node> to <node> 'parameters'
display connect <node> to <node> 'parameters'
display <elemtype> connect <node> to <node> 'parameters'
display element <expr> 'parameters'
display stim at <expr> 'parameters'
(compiled:)
display (ELEMENT, MATCHING, ndt(<node>), color, dscale);
display (<elemtype>, MATCHING, ndt(<node>), zrange1=-10, zrange2=50, color, dscale);
display (<elemtype>, MATCHING, ndt(<node>), VCOLOR, vmax=-0.02, vmin=-0.08);
display (CABLE, MATCHING, ndt(<node>), zrange1=-10, zrange2=50, color, dscale);
display (SPHERE, MATCHING, ndt(<node>), zrange1=-10, zrange2=50, color, dscale);
display (ELEMENT, RANGE, ntd(<node>), ndt(<node>), 'parameters');
display (<elemtype>, RANGEi, ntd(<node>), ndt(<node>), 'parameters');
display (ELEMENT, CONNECT, ndt(<node>) ndt(<node>), 'parameters');
display (<elemtype>, elnum, zrange1, zrange2, color, dscale);
display_stim (at_time, scale);
set_disp_rot( xrot, yrot, zrot, dxcent, dycent, dzcent, rxcent, rycent, rzcent, dsize);
disp_calib (xcalib, ycalib, cline, dsize, dcolor);
setcmap (int *parr, int cmapsize);
setcmap (int cmap);
void display (int elemtype, int disptype, node *nd1, double zrange1, double zrange2,
int dcolor, double(*vpenn)(int elnum, int color),
int cmap, double vmax,double vmin,
double dscale, int hide, int excl, double stime);
void display (int elemtype, int disptype, node *nd1, node *nd2, node *nexc, int exceptype,
double zrange1, double zrange2,
int dcolor, double(*vpenn)(int, int),
int cmap, double vmax,double vmin,
double dscale, int hide, int excl, double stime);
void display (int elemtype, int elnum, double zrange1, double zrange2,
int dcolor, double(*vpenn)(int, int),
int cmap, double vmax,double vmin,
double dscale, int hide);
void display (int elemtype, int elnum, double zrange1, double zrange2,
int dcolor, double dscale);
optional parameters:
xrot = <expr>
yrot = <expr>
zrot = <expr>
color =<expr> max <expr> min <expr>
vpen =<func>
cmap =<expr>
except matching <node>
except <elemtype>
except <elemtype> matching <node>
hide
size =<expr>
dscale=<expr>
rmove (<expr>,<expr>)ltexpr>
center (<expr>,<expr>)
calibline=<expr>
calibline=<expr> loc (<expr>,<expr>)
newpage
where:
parameter: default: meaning
xrot,yrot,zrot 0 degrees x,y,z rotation of anatomical circuit.
color see below color of matching elements displayed.
vpen see below func to compute color of matching elements.
except none prevent display of selected elements.
size 200 um size of display window.
dscale 1.0 display object at different size.
rmove (0,0,0) display object displaced by (x,y,z)
center 1/2 of size location of display window.
z min z1 max n2 none display range from z1 to z2, if backwards, exclude
hide no hide hidden-line removal.
calibline none calibration line in microns
newpage none make new page for movie (use with "vid -P file")
<elemtype> = One of: "cable", "sphere", "synapse","gj",
"rod", "cone", "transducer", "load", "resistor","cap",
"gndcap", "batt", "gndbatt", "chan","vbuf",
"node", "comps".
The display statement is used to display neural circuit
anatomy. The display statement only works in "nc" with the "-d
1" switch (or with "nd"), otherwise all display statements are
ignored. This feature allows you to either display or run a
neural circuit model without changing its descriptor file. You
can display a "photographic" view of your neural circuit using
"nc -d 1 -R" (or "nc -R"), in conjunction with "povray", a 3D
ray-tracing program.
(interpreted:)
at [1][3] loc (10,10) sphere dia 5;
conn [1][3] to [2][4] loc (10,20) cable dia 1 length 10;
(compiled:)
make_sphere (loc(nd(1,3), 10, 10), dia=5);
c = make_cable (nd(1,3), loc(nd(2,4), 10, 20)); c->dia=1;
The "display matching <node>" statement displays all
the neural elements matching the "<node>" value given,
including elements that are located "at" the node or those
that are "connected" to it. A "<node>" value in the
"display" statement can match a neural element with more
node dimensions. In this case, the match ignores the extra
node dimensions. For instance, in the example above, the
statement:
(interpreted:)
display matching [1];
(compiled:)
display (ELEMENT, MATCHING, ndt(1));
matches a "1" in the first dimension, but ignores the
second and third dimensions. In this case, it displays both
the sphere at node [1][3] and the cable from [1][3] to
[2][4]. Any dimension can be specifically excluded from the
match by including a negative number in that dimension. For
example,
(interpreted:)
display matching [1] [-1] [5];
(compiled:)
display (ELEMENT, MATCHING, ndt(1,-1,5));
matches any node with 1 in its first dimension and 5 in
its third dimension. The second dimension is ignored.
Meaning of dimensions
This system of matches is useful when node dimensions
are given specific meanings. It is useful, for example, to
use the first dimension for neuron type, the second
dimension for neuron number, and the third dimension for
morphology within a cell. Then it is possible to display
all neurons of a given type with a simple "display [n]"
statement (where n is the neuron type).
(interpreted:)
display matching [1][3] only;
(compiled:)
void display (ELEMENT, MATCHING, ndt(1,3),
zrange1, zrange2, dcolor, vpen, cmap, vmax, vmin,
dscale, hide, excl=1, stime);
would display only the sphere, not the cable. This is
useful to display a neuron but none of its connections to
other neurons.
display connect [1] to [2];
would display the cable from [1][3] to [2][4]. Any
dimensions not defined by the "display" statement are
ignored, as described above.
Default behavior
The parameters "xrot,yrot,zrot", "size", and "center"
have default values, which are used when no value is given.
If you are defining values for these parameters, you need
only define them once for multiple display statements
because their values are conserved between display statements.
Qualifying the display
The display matching, display range, and display connect
statements may be qualified to an element type by inserting
the element type like this:
(interpreted:)
display matching [5][1]; displays any element type
display sphere matching [5][1]; displays only spheres
(compiled:)
display (ELEMENT, MATCHING, ndt(5,1));
display (SPHERE, MATCHING, ntd(5,1);
Except
The "except" clause allows you to prevent display of a
selected set of elements connected to nodes. The syntax is
the same as for the "matching" statement. Thus:
(interpreted:)
display matching [1][-1][5] except sphere [-1][2];
(compiled:)
display (ELEMENT, MATCHING, ndt(1,-1,5)); except=SPHERE, ndt(-1,2));
This displays all the elements connected to nodes
[1][-1][5] except spheres connected to [1][2][5].
Z max z1 min z2
The "Z max min" clause allows you to display or exclude
neural elements within a range of Z values. If the "max" value is greater
than the "min" value, the clause displays only those neural
elements within the range of z1 - z2. If the "max" value is less
than the "min" value, the clause excludes these neural elements
and displays everything else.
(interpreted:)
display Z max -23 min -20;
(compiled:)
display ( ... zrange1=-23, zrange2=-20, ... );
This displays everything but neural elements in the range
-20 to -23 (microns).
dscale and rmove
Color
Each type of neural element has a default color. The neural element is
displayed in this color when no color parameter is given, or when the color is
zero. If a "color" parameter is given, it sets the color for all neural
elements that are displayed by the statement. The color is reset between
statements so that each statement uses the default color or must have its own
color parameter. Transparency "nocolor"
A special color called "nocolor" is transparent. Any neural elements defined to
have "nocolor" are not displayed. This is useful when you want to display
different parts of a neuron or neural circuit without changing the display
statement. See the "retsim" manual under "density files". A density file
can contain several _COL (color) rows that define different colors for
different cell regions.
Display of voltage, light [Ca], or region with color
Display of photoreceptor pigment type with color
You can display a cone or rod with a color related to its pigment type
by setting its color to "phcolor". Then, during display, the color of
L,M,S pigments are set to red, green, and blue. Rods are displayed in
magenta. Vpen: generate color from function
You can write a display color function and include it on the
display statement. The function must be written with 2
parameters. The first parameter is the element number, and the
second parameter is the color. These parameters depend on the
particular neural element and are automatically passed in when
the function is called. The return value from the function
sets the element's color:
(interpreted:)
func drawv (elnum, color) { /* return color as a func of voltage */
vmin = -0.08;
cmax = 100;
v = V [element elnum->node1a][element elnum->node1b]; /* voltage at node1 */
vs = v-vmin;
if (vs<0) vs=0;
if (vs>cmax) vs=cmax;
if (color != blue) {
color = int(vs*100);
}
return color;
};
display cable matching <node> vpen drawv;
(compiled:)
double drawv (int elnum, int color) { /* return color as a func of voltage */
int cmax;
double v, vs, vmin;
elem *e;
vmin = -0.08;
cmax = 100;
e = elempnt(elnum);
v = v (e->node1a, e->node1b); /* voltage at node1 */
vs = v-vmin;
if (vs<0) vs=0;
if (vs>cmax) vs=cmax;
if (color != blue) {
color = int(vs*100);
}
return color;
}
display (CABLE, MATCHING, <node>, drawv);
Display stim
To display a light stimulus, use the "display stim" statement.
This statement displays the light intensity at each photoreceptor
at the photoreceptor's (x,y) location. The intensity is coded in
color using a lookup table, with white and red the maximum and
blue the minimum intensities. The stimulus may originate from a
".t" stimulus file generated by "stim" or may originate entirely
from "nc" itself without any stimulus file. The stimulus may be
created by the "stim spot", "stim bar", "stim sine", "stim
gabor", "stim sineann", "stim windmill", "stim rod", or "stim
cone" statements.
You can display what the stimulus would look like at a future
time without running the simulation with "step" or "run". This
allows you to "play" the stimulus without taking the time to run
the simulation. To display the stimulus in this way, use an
expression for the time at which to display:
(interpreted:)
stim spot ...
disp stim at <time>;
(compiled:)
stim_spot (...);
display_stim (time, dscale);
The advantage of this method is that you can see the stimulus
at a distant time in the future, without running the full
simulation, which is typically much faster.
stim spot ... start <expr> dur <expr>;
step <expr>;
disp stim;
disp stim at <time> dscale <expr>;
where for good visibility one sets <expr> between 2 and 10.
Colormaps
Colormap N val
1 16 0-15 (VGA colors, black,blue,green,cyan,red,magenta,brown,white, etc., for plots)
2 16 16-31 (blue=low, green=med low, yellow=med hi, red=high, for vcolor, cacolor, etc.)
3 32 32-63 (blue=low, green=med low, yellow=med hi, red=high, high-res, for PSPS, spikes, etc.)
4 16 64-79 (blue=low, purple=medium, red=high, for vcolor, cacolor, etc.)
5 16 80-95 (black=low, red=high, for vcolor, cacolor, etc.)
6 16 96-111 (black=low, green=high, for vcolor, cacolor, etc.)
7 16 112-127 (black=low, blue=high, for vcolor, cacolor, etc.)
8 100 128-227 (for "display stim" grayscale)
9 100 228-327 (a bigger variety, taken from "X11/rgb.txt", see ccols2.txt )
10 (user defined, must use colors defined above, i.e. 0-295)
1 350 ("nocolor", i.e. transparent, not in colormaps)
(interpreted:)
dim mycolormap = {{1,2,3,4,5,32,6,65,8}};
display cmap = mycolormap;
display matching [2][-1] pen 5; /* displays color 32, dark gray */
(compiled:)
int mycolormap[] = {1,2,3,4,5,32,6,65,8};
setcmap(mycolormap,sizeof(mycolormap));
display (ELEMENT, MATCHING, ndt(2,-1), pen=5; dscale=1); /* displays color 32, dark gray */
Display anatomy, stim, vcolor, cacolor in
construction mode
for (t=0; t<stoptime; t++ ) {
modify neural circuit ...
step <expr>;
disp stim;
}
or
for (t=0; t<stoptime; t++ ) {
display stimulus ...
step <expr>;
disp stim;
}
Making movies
frameint = 0.001;
(interpreted:)
proc onplot() /* plot procedure that displays a neuron's voltage */
{
if ((int(time/ploti+0.001) % (frameint/ploti)) == 0) {
display matching [celltype][cellnum][-1] color=vcolor min=-0.09 max=0.02;
draw_color_scalebar(cmin,cmax);
display newpage;
};
};
(compiled:)
void onplot(void) /* plot procedure that displays a neuron's voltage */
{
if ((int(time/ploti+0.001) % (frameint/ploti)) == 0) {
display (ELEMENT, MATCHING, ndt(celltype,cellnum,-1), color=vcolor, min=-0.09, max=0.02);
draw_color_scalebar(cmin,cmax);
gpage();
}
}
.
.
.
setonplot(onplot); /* set onplot() procedure to run at plot time */
The basic idea is to display the voltage in the network at an
interval that may be slower than the standard plot interval
defined by "ploti". In the above example, the display is
triggered at an an interval of "frameint", or 1 ms. Note that
the statement "display newpage" defines the end of a frame. For
other uses of the "onplot()" procedure, see "Run procedure at
plot time".
proc draw_time(dtime)
{
if (dtime < 1e-6 && dtime > -1e-6) dtime = 0;
gframe ("Col_bar");
gpen (0);
gmove(0.10,0.025);
gtext ("V at time t=%g s",oldtime);
gpen (15);
gmove(0.10,0.025);
gtext ("V at time t=%g s",dtime);
oldtime = dtime;
gframe ("..");
};
proc draw_color_scalebar(cmin,cmax)
/* Draw scalebar for vcolor display */
{
local colbarlen,dist,wid;
local colbase,numcols;
local x1,y1,x2,y2,x3,y3,x4,y4;
local dim colors[10][2] = {{0,0,0,16,16,16,32,16,48,16,64,16,80,16,96,100,148,100,0,0}};
/* see colormap in manual */
colbarlen=0.40;
wid = 0.03;
colbase = colors[colrmap][0]; /* lowest color in colormap */
numcols = colors[colrmap][1]; /* number of colors used */
dist = colbarlen/numcols;
gframe ("Col_bar");
for (i=0; i<numcols; i++){
gpen(i+colbase);
x1 = i*dist; y1 = wid/2;
x2 = (i+1)*dist; y2 = y1;
x3 = x2; y3 = -wid/2;
x4 = x1; y4 = y3;
grect(x1,y1,x2,y2,x3,y3,x4,y4,fill=1);
};
gmove(-0.1,-0.002);
gpen (15);
gtext("MIN");
gmove(-0.1,-0.03);
sprintf (nbuf,"%.3g",cmin); /* lowest value */
gtext(nbuf);
gmove(colbarlen+0.05,-0.002);
gtext("MAX");
gmove(colbarlen+0.05,-0.03);
sprintf (nbuf,"%.3g",cmax); /* highest value */
gtext(nbuf);
gframe ("..");
draw_time(time);
};
if (make_movie) {
gframe ("Col_bar");
gorigin (0.15,0.05); /* set bar position */
gframe ("..");
oldtime = 0;
};
Making movies with different simultaneous views
To make a movie with 2 views of the same neuron, you initialize 2 sub-frames,
each with a different location within the movie frame. See the original source
code in "onplot_movie.cc". This procedure is run from the experiment file.
} else if (dend_layers) { /* dual disp volts, na inact; or 2 dend layers */
gframe ("/movie");
gorigin (0.15,0.55); * movie smaller, halfway up */
gsize (0.5);
gmove (0.05,0.85);
gpen (textcol); // write white on black, black on white
gtext (movie_title1);
gframe ("time");
gorigin(0.60,0.85); /* set time position */
gframe ("..");
gframe ("..");
gframe ("/movie2");
gorigin (0.15,0.25); /* movie smaller, bottom */
gsize (0.5);
gmove (0.05,0.8);
gpen (textcol); // write white on black, black on white
gtext (movie_title2);
gframe ("..");
gframe ("/gc_col_bar");
gorigin (0.90,0.45); /* set bar position */
gframe ("..");
}
if (volt_map) drawvcolscale("gc_col_bar",Vmin,Vmax,"V",colormap);
Then at run time, the "onplot()" procedure updates the separate views
while the model is running. The "set_rcolors procedure sets the "rcolors"
variable to the appropriate _COL row in the density file, so the display
will show the different region colors defined in different _COL rows:
else if (dend_layers) { // make movie of 2 separate dendritic layers
gframe ("/movie"); // show first layer
draw_time(simtime);
_COL = denddens_color1; // set colors in density file
set_rcolors(rec_ct,rec_cn); /* set region colors */
if (inputs_backgr && show_inputs) draw_inputs();
display(MATCHING,ndt(rec_ct,rec_cn,-1), only=1, color=voltmap_color1,
vmax=Vmax,vmin=Vmin,cmap=colormap,dscale=1);
_COL = denddens_color1t; // set colors in density file for labels
set_rcolors(rec_ct,rec_cn); /* set region colors */
display (LABEL, MATCHING, ndt(rec_ct,rec_cn,-1), node_color=RCOLOR, dsgc_nscale);
if (!inputs_backgr && show_inputs) draw_inputs();
gframe ("..");
gframe ("/movie2"); /* show second layer */
_COL = denddens_color2; // set colors in density file
set_rcolors(rec_ct,rec_cn); /* set region colors */
display (MATCHING,ndt(rec_ct,rec_cn,-1), only=1,color=voltmap_color2,
vmax=Vmax,vmin=Vmin, cmap=colormap,dscale=1);
_COL = denddens_color2t; // set colors in density file for labels
set_rcolors(rec_ct,rec_cn); /* set region colors */
display (LABEL, MATCHING, ndt(rec_ct,rec_cn,-1), node_color=RCOLOR, dsgc_nscale);
gframe ("..");
}
To make some regions transparent in one view but visible in another view, you
can set up 2 or more _COL rows in the density file. To display regions
as a heat map of voltage (or another state variable) you set their color to
"vcolor". To make regions transparent, set their color to "nocolor".
_COL original region colors
_COL2 all regions displayed in heatmap colors
_COL3 R2,R5,R6 => heatmap colors, R1,R3,R4 => transparent
_COL4 R1,R3,R4,R6 => heatmap colors, R2,R5 => transparent
_COL5 R2,R5,R6 => white, R1,R3,R4 => transparent, for label text (on black background)
_COL6 R1,R3,R4,R6 => white, R2,R5 => transparent, for label text (on black background)
Rows in the density file:
0 R1 R2 R3 R4 R5 R6 R7 R8 R9 R10
_COL blue red cyan brown green magenta blue yellow brown red ltred # color
_COL2 vcolor vcolor vcolor vcolor vcolor vcolor blue yellow brown red ltred # color
_COL3 nocolor vcolor nocolor nocolor vcolor vcolor blue yellow brown red ltred # off_layer color
_COL4 vcolor nocolor vcolor vcolor nocolor vcolor blue yellow brown red ltred # on layer color
_COL5 nocolor white nocolor nocolor white white blue yellow brown red ltred # label off layer color
_COL6 white nocolor white white nocolor white blue yellow brown red ltred # label on layer color
Displaying the movie
You can view the output in graphics mode as usual by:
nc .... -v script.n | vid
To study the movie more carefully, you may want to slow down the
display further, using the "-S" command line option for "vid":
nc .... -v script.n | vid -S 1.5
This example displays individual frames with an interval of at least 1.5 seconds.
Note that for this to work correctly, individual frames must be
defined as in the "display newpage" command in the example above.
Making the movie frames in separate files
To make a movie from separate files, define a file name using the
-P command line option:
for a black background:
nc .... -v script.n | vid -c -B 0 -P cellmovie
or for a white background:
nc .... -v script.n | vid -c -B 7 -P cellmovie
This will create the set of files: "cellmovie_0001.ps, cellmovie_0002,ps,
... cellmovie_000N.ps" that you can convert to other image formats.
For example, the programs, "makempeg", "mpeg2encode", or "ffmpeg",
available on the web, make movies from "gif" or "ppm" files
respectively. You can convert from PS format using a converter
like ps2ppm:
#! /bin/tcsh -f
#
# ps2ppm
#
# script to make .ppm files from .ps or .eps
#
foreach i ($argv)
echo "converting $i to $i:r.ppm"
cat $i | gs -q -dNOPAUSE -r100 -sDEVICE=ppm -sOutputFile=- - > $i:r.ppm
end
Making the .mpg movie file
To automatically make a movie from the set of .ps files, you can run
"make_movie_mpg". This runs the above ps2ppm command to generate .ppm (bitmap)
files from the original .ps files, then integrates changes in the separate
frames for continuity in the movie, and then runs ffmpeg to create the movie.
These commands are located in nc/bin:
#! /bin/csh -f
#
# make_movie_mpg
#
foreach i ($argv)
echo $i
make_movie3c $i
make_movie3d $i
rm $i*_????.ps $i*_????.ppm
end
make_movie3c:
#!/bin/bash
#
# make_movie3c
#
ps2ppm $1_????.ps
cnt=0
#count files
for file in `find ./ -name "$1_????.ps"`
do
fname=`basename $file`;
dname=`dirname $file`;
fullname=$dname/$fname;
cnt=$(($cnt+1))
#echo "cnt=$cnt, $fullname";
done
# blend together backgrounds using movconvert
movconvert -f $1_ -n $cnt
# join .ppms together into video
# ffmpeg -f image2 -i $1_%04d.ppm $1.mpg
The "movconvert" command integrates changes in separate frames for the movie.
Its source code is located in nc/src -- you can make it with "make movconvert,
then link its binary into nc/bin:
cd nc/src
make movconvert
ln movconvert ../bin
#!/bin/bash
#
# make_movie3d
#
ffmpeg -f image2 -i $1_%04d.ppm $1.mpg
Making a movie of the stimulus
To make a movie from the stimulus display, you must run the "display_page()"
procedure after displaying every frame. This sends the current display out to a
frame for "vid".
Then you enable DMOVIE (32) in the "-d " command-line switch. Since "-d 16"
displays the stimulus, you add 16+32 = 48.
For example,
nc ... -d 48 script.n | vid -B 0 -c -P filename
or
retsim ... -d 48 script | vid -B 0 -c -P filename
Then you run "make_movie_stim", which is similar to make_movie_mpg, except that it does not run "movconvert", as the stimulus display contains no partial display of objects that need to be integrated.
#!/bin/bash
ps2ppm $1_????.ps
#join .ppms together into video
ffmpeg -f image2 -i $1_%04d.ppm $1.mpg
make_movie_stim filename
This will convert the .ps files into the equivalent .ppm frame files, and then will run "ffmpeg" to convert the frames into a .mpg movie file.
Displaying node numbers
To display node numbers in their proper 3D locations, insert
the keyword "node" as a qualifier. You can vary the size of the
displayed number with the "dscale" parameter.
(interpreted:)
display node matching [5] dscale 2; displays node numbers
(compiled:)
display (NODE, MATCHING, ndt(5), color=5, dscale=2);
For multidimensional nodes, to display just one
of the numbers, negate it and subtract the dscale parameter
divided by 10. The example below displays the second node dimension
(usually the cell number) with an effective "dscale" of 1.5:
(interpreted:)
display node matching [5][-1][-1] dscale -2.15;
(compiled:)
display (NODE, MATCHING, ndt(5), color=5, dscale= -2.15);
You can display these node number sequences:
number displayed node numbers (dimensions)
1 1
2 2
3 3
4 4
5 1,2
6 2,3
7 1,2,3
So, for example, to display the cell number (second node dim)
and the node number within the cell (third node dim) with a
size of 1.5:
display node matching [5][-1][-1] dscale -6.15;
Displaying compartments
To display compartments and their connections, insert the
keyword "comps" as a qualifier. Then use the variable "disp" or
the command line switch "-d n" (n=1-4, see Section 6, "nc") to
display various combinations of neural elements, compartments or
connections. The rationale for this scheme is that one often
would like to change what objects are displayed without
modifying the script.
(interpreted:)
display comps matching [5][1];
(compiled:)
display (COMPS, MATCHING, ndt(5,1));
This statement displays only compartments and/or their low-
level connections that have been translated from neural elements
matching a node. A compartment is displayed as a sphere with a
size that would have the compartment's resistance and capacitance.
A connection is displayed as a yellow line between compartments.
The compartment and connection display is useful for "tuning" the
variable "lamcrit" which controls the minimum size of
compartments. Redefining neural element icons
To re-define the "icon" used to display a neural element,
put a procedure like one of these in your "nc" script file, in a location
in the file before the display statement:
(interpreted:)
proc phot_dr (type, pigm, color, dscale, dia, foreshorten, hide) {
gpen (color);
gcirc (dscale*dia/2,0);
};
proc gapjunc_dr (color, dscale, length, foreshorten, hide) {
gpen (color);
gcirc (dscale*dia/2,0);
};
proc synapse_dr (color, vrev, dscale, dia, length, foreshorten, hide) {
local dx,dy;
dx = length; dy = dscale*dia/2;
gpen (color);
grect (dx,0,dx,dy,-dx,dy,-dx,0);
gmove (0,0);
gcirc (dscale*dia/2,0);
};
proc elec_dr (color, dscale, dia, length, foreshorten, hide, elnum) {
gpen (color);
gcirc (dscale*dia/2,0);
gmove(0,02,0);
n2 = elem elnum->node1b;
n3 = elem elnum->node1c;
sprintf (numbuf,"%d %d",n2,n3);
gtext (numbuf);
};
(compiled;)
void phot_dr (type, pigm, color, dscale, dia, foreshorten, hide) {
gpen (color);
gcirc (dscale*dia/2,0);
};
set_phot_dr(phot_dr);
void gapjunc_dr (color, dscale, length, foreshorten, hide) {
gpen (color);
gcirc (dscale*dia/2,0);
};
set_gapjunc_dr(gapjunc_dr);
void synapse_dr (synapse *spnt, color, vrev, dscale, dia, length, foreshorten, hide) {
double dx,dy;
dx = length; dy = dscale*dia/2;
gpen (color);
grect (dx,0,dx,dy,-dx,dy,-dx,0);
gmove (0,0);
gcirc (dscale*dia/2,0);
};
set_synapse_dr(synapse_dr);
void elec_dr (color, dscale, dia, length, foreshorten, hide) {
elem *epnt;
node *np;
gpen (color);
gcirc (dscale*dia/2,0);
gmove (0.02,0);
epnt = findelem(elnum);
if (dscale != 1 && np=epnt->nodp1)
dr_node(np,dscale);
};
set_elec_dr(elec_dr);
Currently only photoreceptor ("phot_dr"), gap junction
("gapjunc_dr"), synapse ("synap_dr"), and recording electrode
("elec_dr") icons can be re-defined. It is easy to add new
procedures in the "nc" source code for other neural elements.
Draw synapses with cell numbers
In a complicated circuit, it is sometimes helpful to label the synapses
with both the presynaptic and postsynaptic cell number. You can do this
by defining an alternate "synapse_dr()" procedure:
#include "gprim.h"
void syn_draw2 (synapse *spnt, int color, double vrev, double dscale, double dia,
double length, double foreshorten, int hide)
/* draw synapse within small oriented frame */
{
int fill=1;
double tlen;
char tbuf[10];
dia *= dscale; /* draw circle with line */
if (dia < 0) dia = -dia;
color = -1;
if (color < 0) {
if (vrev < -0.04) color = RED;
else color = CYAN;
}
gpen (color);
if (length > 1e-3) {
gmove (length/2.0,0.0);
if (dia > 0.001) gcirc (dia/2.0,fill);
else gcirc (0.001,fill);
gmove (0,0);
gdraw (length,0);
}
else gcirc (0.001,fill);
gpen (black);
sprintf (tbuf,"%d %d",spnt->node1b,spnt->node2b); /* print pre and postsynaptic cell number */
tlen = strlen(tbuf);
gmove (length/2.0 -tlen*0.3, -1.0);
gcwidth (1.2);
gtext (tbuf);
}
You can activate this procedure with:
set_synapse_dr (syn_draw2);
placed in the script before the display is run.
transf function
tarr = transf (x,y,z);
xt = tarr[0];
yt = tarr[1];
zt = tarr[2];
Elabl
The "elabl" (element label) clause allows a neural element to
be labeled by a name (string). The name need not be unique so it
is useful for setting categories of parts of a neuron, for
example, "soma", "axon", and "dendrite".
(interpreted:)
conn <node1> to <node2> cable <membrane params> elabl <expr>
(compiled:)
c = conn(<node1>, <node2>, CABLE); <membrane params> c->elabl <string>
The "elabl" name can be retrieved later with the
element <expr> -> elabl
clause (see"element fields" below).
Ename
The "ename" clause allows a neural element to be accessed
by a unique identifier (number), either for later selection,
modification, or display.
(interpreted:)
conn <node1> to <node2> synapse <synaptic params> ename <var>
(compiled:)
s=conn(<node1>, <node2>, SYNAPSE); <synaptic params> var=s->elnum;
A unique identifier is assigned to the variable whose
name is given after the "ename" keyword. That specific
individual neural element can be referred to later by the
variable's value.
(interpreted:)
func na_inact () /* returns total inactivated fraction for Na type 2*/
{
return (G(7)var + G(8)var + G(9)var);
}
(compiled:)
double na_inact (void) /* returns total inactivated fraction for Na type 2*/
{
return (record_chan(var,G,7) + record_chan(var,G,8) + record_chan(var,G,9));
}
Modify
The "ename" and "modify" clauses allow certain neural
elements to be modified during a simulation after they have
been created. The "synapse", "gj", and "receptor" neural
elements can be modified (between "step" statements) with
the following syntax:
In the original declaration:
(interpreted:)
conn <node1> to <node2> synapse <synaptic params> ename <var>
where
<synaptic params> are the optional paramaters originally
used for specifying the synapse;
<var> is a variable used for remembering
the synapse especially for modifying later.
In a later declaration:
modify <expr> synapse <new synaptic params>
where
<new synaptic params> are the new parameter value specifications;
<expr> is an expression having the value of
the "var" in the "ename" statement
described above. Ordinarily, this
expression is simply the variable.
(compiled:)
In the original declaration:
s = (synapse *)conn (nd(<node1>), nd (<node2>), SYNAPSE); <synaptic params>
var = s->elnum;
In a later declaration:
s = (synapse *)makelem(SYNAPSE,modify (var)); <new synaptic params >
With the "ename/modify" feature, one can change a synapse as
a function of any other recordable or computable parameter in a
neural circuit. For instance, one could vary postsynaptic
conductance (or presynaptic transmitter release) as a delayed
function of postsynaptic voltage to simulate long-term
potentiation.
Modifying synaptic parameters during a run
In order to change synaptic parameters dynamically, i.e.
during a simulation, it is necessary to stop the simulation
"run" mode and return to "construction" mode. Then the
appropriate modifications can be made to neural elements and
the simulation can be restarted. This is usually done with
a "for" loop, with the modification statements and a "step"
statement inside the loop.
(interpreted:)
pre = 1;
post = 2;
soma = 3;
synstep = .01; /* timestep for synaptic modification */
at [pre] sphere dia 5;
conn [pre] to [post] synapse expon 2 thresh= -.045 maxcond=1e-9 ename syn1;
conn [post] to [soma] cable dia .2 length 10;
at [soma] sphere dia 10;
stim node [pre] cclamp 1e-10 start 0.2 dur 10;
for (t=0; t<100; t+= synstep) {
newcond = modsyn (pre,post); /* function to calc new conductance */
modify syn1 synapse maxcond=newcond;
step synstep;
};
(compiled:)
pre = 1;
post = 2;
soma = 3;
synstep = .01; /* timestep for synaptic modification */
make_sphere(nd(pre), dia=5);
s=make_synapse (nd(pre), nd(post)); s->ngain=2 s->thresh= -.045; s->maxcond=1e-9; syn1=s->elnum;
c=make_cable(nd(post), nd(soma)); c->dia=0.2; c->length=10;
make_sphere(nd(soma), dia=10);
cclamp (ndn(pre),1e-10,start=0.2,dur=10);
for (t=0; t<100; t+= synstep) {
newcond = modsyn (pre,post); /* function to calc new conductance */
s = (synapse *)makelem(SYNAPSE,modify (syn1)); s->maxcond=newcond;
step(synstep);
}
When neither the synapse pointer or its element number are
available, you can use the "foreach()" function to search
for the right one. For example, if you want to find and modify
the output synapses of a population of cells with nodes [prect][precn],
you can do it like this:
int prect, precn;
for (epnt=elempnt; epnt=foreach(epnt,SYNAPSE,prect,-1, NULL,&precn);
epnt=epnt->next)
{
synapse *s;
printf ("found synapse from cell [%d][%d]\n",prect,precn);
syn1 = get_efield(epnt,ELNUM);
s = (synapse *)makelem(SYNAPSE,modify (syn1)); s->maxcond=newcond;
}
Or if you want to find the synapse that connects to
postsynaptic node [postct][postcn], you could do it like this:
int postct, postcn;
for (epnt=elempnt; epnt=foreach(epnt,SYNAPSE,-1,-1, NULL,NULL);
epnt=epnt->next)
{
if (get_efield (epnt,NODE2A)==postct) &&
get_efield (epnt,NODE2B)==postcn)) syn1 = get_efield(epnt,ELNUM);
}
Then, you could modify that synapse as above:
s = (synapse *)makelem(SYNAPSE,modify (syn1)); s->maxcond=newcond;
Erase
(intepreted:)
erase model
erase array
erase node <node>
erase element <element>
(compiled:)
node *erasenode(node *npnt);
void eraseelem(elem *epnt);
void erase(node *npnt);
void erase(elem *epnt);
void eramod(void);
Save, Restore
(interpreted:)
save model (<filname>)
restore model (<filname>)
(compiled:)
void savemodel (char *filnam);
void restoremodel (char *filnam);
sprintf (savefilnam,"file%06g",getpid()); # to add pid to file name
save model (savefilnam); # creates "file024994"
or
sprintf (savefilnam,"file%04g%06g",int(rand()*10000),getpid()); # to add rand num, pid
save model (savefilnam); # creates "file3032024994", pid = 024994
.
.
.
restore model (savefilnam); # restores model to original state
Run_on_exit
To erase the save file after you've stopped the model either with
^C at the terminal, or with a "kill
(interpreted:)
proc run_on_exit()
/* procedure that runs just before exit */
{
sprintf (str,"unlink %s",savefilnam);
system(str); # remove the temporary save file
};
(compiled:)
void on_run_exit (void)
/* procedure that runs just before exit */
{
unlink (savefilnam); # remove the temporary save file
}
# Below, at beginning of main model procedure:
set_run_on_exit(run_on_exit); # Initialize "run_on_exit()" to run just before exit
# when program is stopped with ^C or "kill" command.
Run_on_step
To run an extra part of the model in a predefined subroutine, once per time step,
you can write a "run_on_step" subroutine:
(interpreted:)
proc run_on_step()
/* procedure that runs every time step */
{
};
(compiled:)
void on_run_step (void)
/* procedure that runs every time step */
{
}
# Below, at beginning of main model procedure:
set_run_on_step(run_on_step); # Initialize "run_on_step()" to run each time step
Run and Step
The run statement causes the simulated neural circuit to
be activated, and also activates any "stimulus" and "plot"
statements. The simulator numerically integrates voltrages
over time and also activates stimuli and plots at their
proper times. The simulator stops when the "time" variable
reaches the value of "endexp" (end of the experiment).
"graph" and "record" statements are not activated during a
run. A second "run" statement in a program is allowable but
after the first "run" statement, time is reset to
zero and all neural circuits are erased.
(interpreted:)
step <expr>
run;
(compiled:)
step(<expr>);
run();
where:
step <expr> (sec) = time interval to run simulation
The "step" statement works exactly like the "run"
statement (it activates the neural circuit, stimuli, and
plots) but stops after a time interval, allowing the network
to be restarted with where it stopped. All parameters such
as node voltages and the elapsed simulation time retain
their values.
Note on use of "step" with "stim" statement:
If you step a nonintegral multiple of "timinc", the
actual time run by the "step" statement may be up to one
extra "timinc":
timinc = 0.0001;
steptime = 0.011111111111; /* not integral mult of timinc */
for (i=1; i<n; i++) {
plotarr[i] = V[node1];
stim .... start=i*steptime dur=steptime; /* off by 0.0001 each time */
step steptime; /* steps 0.0112 sec each time */
};
For example, if timinc=1e-4 and you give a time step of
0.01111111, the simulator will run for 0.0112 sec which is
the next larger interval. This is usually not a problem,
but if you place the "step" statement inside a "for" loop
along with "stim" statements, you may find that the stimuli
are not being started at the correct times because of the
"roundoff" problem stated above. The way to correct this
problem is to make 2 separate "for" loops, one to generate
the stimuli, and one to run the "step" statement:
steptime = 0.011111111111; /* not integral mult of timinc */
for (i=1; i<n; i++) {
stim .... start=i*steptime dur=steptime; /* correct to 0.0001 sec */
};
for (i=1; i<n; i++) {
plotarr[i] = V[node1];
step steptime; /* step 0.0112, but maybe acceptable */
};
When the "stim" statements are all executed before the
first "step" statement, they are all run in "construction
mode" before the model starts, so they are correctly
synchronized with the integration time step. Another
solution is to use the "time" variable which always has the
correct time updated by the "step" statement:
steptime = 0.011111111111; /* not integral mult of timinc */
for (i=1; i<n; i++) {
plotarr[i] = V[node1];
stim .... start=time dur=steptime; /* may give blank betw. stimuli */
step steptime; /* still steps 0.0112 sec */
};
NeuronC programming statements
NeuronC contains a subset of the "C" programming
language. This subset includes:
for
while
if
else
assignment
define procedure, function
call procedure, function
return
break
continue
formatted print
arithmetic and logical operators
increment operators
numeric expressions
trig, log, expon, power, sqrt functions
predefined constants (PI, E, etc.)
include file
edit file
run system command
automatic variable definition
local variables
dynamically allocated multidimensional arrays
Features of C not supported:
structures, unions, bit fields
pointers, address operators
#define, #ifdef statements
Most of the statements in NeuronC borrowed from C
are familiar to most of us who have used C. There are
a few significant exceptions. A semicolon must be used
after every statement in NeuronC except the first
statement after the "if" in an "if () ... else ... "
statement. For example:
if (i > 5) x = 0
else x = 1;
These two lines comprise a single statement and the
semicolon (";") is missing after the first line to
allow NeuronC to better sense the upcoming "else".
for (i=0; i>5; i++) {
x[i] = i;
y[i] = array[i];
}; /* semicolon necessary */
NeuronC advanced programming
Node fields
interpreted:
node <node> -> exist 1 if node exists, 0 if not
node <node> -> numconn Number of connections to elements
node <node> -> numsyn Number of connections to synapses
node <node> -> xloc X location
node <node> -> yloc Y location
node <node> -> zloc Z location
node <node> -> cacomp 1 if node has cacomp, 0 if not.
node <node> -> <expr> Absolute number of an element,
given its sequence number at node.
node <node> -> synapse <expr> Absolute number of a synapse,
given its sequence number at node.
compiled:
get_nfield (<node>, <nodefield>);
get_nfield (<node>, <nodefield>, <elnum>);
where: <node> is a pointer to an element
<elnum> is the element number, when
<nodefield> is the field name (integer), one of:
ELNUM EXIST NUMCONN NUMSYN SYNAPSE XLOC YLOC ZLOC CACOMP
When the field is ELNUM or SYNAPSE, the <elnum> field is
the element relative to the node (i.e. 1...n ).
Once nodes are created, they contain information about
their location and connections, called "node fields". It is
sometimes useful to retrieve this information directly from
its storage in the node instead of referring back to the
original algorithm that created the node. The concept of a
"pointer" serves this purpose. To retrieve information from
a node field, enter a node number, then the characters "->"
and one of the "node fields". For instance:
node [50][1] -> xloc
means the numerical x location of node [5][1]. This can
be used in any expression where a number would normally be
required, and can be part of arithmetic or passed to a
function. A node's location is useful when a NeuronC
program is determining how close two neurons are to each
other when building a circuit. Remember, node numbers may
be 1-, 2-, 3-, or 4-dimensional.
ncon = node [50][2] -> numconn;
for (i=0; i<ncon; i++) { /* look for first cable */
elnum = (node [50][2] -> i);
if (element elnum->type == "synapse") break;
};
othernode = element elnum->node2b;
if ((nsyn = (node [50][2] -> numsyn)) > 0)
elnum = (node [50][2] -> synapse 1);
};
othernode = element elnum->node2b;
element fields
interpreted:
element <element> -> type element type: "cable","sphere","chan", etc.
element <element> -> ntype numerical element type.
element <element> -> elabl label for element (set by "elabl" clause)
element <element> -> dia diameter.
element <element> -> length length, given or calculated from nodes.
element <element> -> n3dist 3D distance between element's nodes.
element <element> -> n2dist 2D (x,y) distance between element's nodes.
element <element> -> rm membrane Rm.
element <element> -> ri membrane Ri.
element <element> -> cplam lambda for compartments in cable.
element <element> -> maxcond maxcond for a synapse or channel.
element <element> -> node1a number of first node.
element <element> -> node1b
element <element> -> node1c
element <element> -> node1d
element <element> -> node2a number of second node.
element <element> -> node2b
element <element> -> node2c
element <element> -> node2d
To retrieve information about a neural element, enter
"element", then the element number, then place the characters
"->" after the element number, and then place a field name. This
expression can be used anywhere instead of a standard numerical
expression.
compiled:
get_efield (<elem>, <elemfield>);
get_efield (<elnum>, <elemfield>);
where: <elem> is a pointer to an element
<elnum> is the element number (integer)
<elemfield> is the field name (integer), one of:
ELNUM NTYPE LENGTH N3DIST N2DIST N2DIST DIA DIA2 RM RI CM CPLAM
MODIFY MAXCOND SCURVE SDYAD DYAD NUMDYAD NUMSPRE
NODE1A NODE1B NODE1C NODE1D
NODE2A NODE2B NODE2C NODE2D
chan fields
To retrieve information about a channel element, enter "chan",
then the channel element number, and then place the characters
"->" after the element number, and then a field name:
chan <element> -> type element type: "Na","K", "KCa" etc.
chan <element> -> ntype numerical channel type.
chan <element> -> stype numerical channel sub-type.
chan <element> -> nstate number of states in Markov channel.
chan <element> -> maxcond maxcond for a channel.
ntype() function
x = ntype (<elemtype>)
The numerical "element <element> -> ntype" expression
returns a number unique to the type of the neural element.
To find out what type this number is, you can compare it
with "ntype(<elemtype>)", where <elemtype> is one of the
neural element types (see <elemtype> in
"foreach" below).Distance functions
(interpreted:)
x = n2dist (<node1>, <node2>) 2D (x,y) node distance function
x = n3dist (<node1>, <node2>) 3D node distance function
x = nzdist (<node1>, <node2>) 1D Z node distance function
(compiled:)
x = dist2d (<node1>, <node2>) 2D (x,y) node distance function
x = dist3d (<node1>, <node2>) 3D node distance function
x = distzd (<node1>, <node2>) 1D Z node distance function
These functions compute the distance between 2 nodes when
their locations have been defined. The node numbers may be 1, 2,
3 or 4 dimensional, and the extra dimensions not used are
assumed, for the computation, to be zero. n3dist measures 3D
distance in (x,y,z), and n2dist measures distance in (x,y) only,
useful for developing rules for "growing" neurons.
(interpreted:)
x = e2dist ( <node>, <element> ) 2D element distance function
x = e3dist ( <node>, <element> ) 3D element distance function
x = ezdist ( <node>, <element> ) Z dist element distance function
(compiled:)
x = endist2d ( <node>, <element> ) 2D element distance function
x = endist3d ( <node>, <element> ) 3D element distance function
x = endistzd ( <node>, <element> ) Z dist element distance function
These functions compute the distance between a node and an
element. If the closest part of the element is one of its end
nodes, the distance to that node is returned. e3dist measures 3D
distance in (x,y,z), and e2dist measures distance in (x,y) only,
useful for developing rules for "growing" neurons.Fractional distance along a cable
x = efrac ( <node>, <element> ) fractional distance on cable
This function finds the point in a cable closest to the given
node. It returns the fractional distance from this point to the
cable's "first" end node. The distance ranges between 0 and 1, so
if the closest part of the element is the first end node, 0 is
returned, and if it is the second end node, 1.0 is returned.
at <node> : <element> offset <expr> put <node>
This statement puts a new node on a cable at the
specified "offset". The offset is a fraction between 0 and
1 and can be computed by the "efrac()" function. The new
node splits the cable element into two cables, each with a
new length according to the location of the new node with
respect to the existing nodes' positions.
foreach statement
(interpreted:)
foreach <elemtype> ?var statement (iterate over element type)
foreach <elemtype> ?var node <nodedim> statement (iterate over elem, return node)
foreach node <nodedim> statement (iterate over matched nodes)
foreach <elemtype> ?var within <expr> node <nodedim> statement (iterate over elem type within radius)
foreach <elemtype> ?var node <nodedim> within <expr> node <nodedim> statement (iterate over elem, return node within radius)
foreach node <nodedim> within <expr> node <nodedim> statement (iterate over matched nodes within radius)
where:
<nodedim> = 1 to 4 node dimensions, each in the following syntax:
[<expr>] dimension set to a value that must match.
?var dimension free to vary, not to be matched.
The "?" in front of the variable means the variable
will be replaced with the corresponding value (from
the node that matches) for that dimension while the
following statement is executed.
<elemtype> = One of: "element", "cable", "sphere", "synapse",
"gj", "rod", "cone", "load", "resistor",
"cap", "gndcap", "batt", "gndbatt", "chan",
"vbuf".
within = "within2d" or "within3d"
(compiled:)
for (epnt=elempnt; epnt=foreach(epnt,<elemtype>); epnt=epnt->next) {} (iterate over element type)
for (epnt=elempnt; epnt=foreach(epnt,<elemtype>,<nodedim>, <nodedimpnt>); (iterate over elem, return node)
epnt=epnt->next) {}
for (epnt=elempnt; epnt=foreach(epnt,<elemtype>,<nodedim>, <nodedimpnt>, (iterate over elem, return node within radius)
radius, distfunc, <rnode>); epnt=epnt->next) {}
for (npnt=nodepnt; npnt=foreach(npnt,<nodedim>, <nodedimpnt>); (iterate over matched nodes)
epnt=epnt->next) {}
for (npnt=nodepnt; npnt=foreach(npnt,<nodedim>, <nodedimpnt>, (iterate over matched nodes within radius)
radius, distfunc, <rnode>); epnt=epnt->next) {}
where:
<nodedim> = 4 node dimensions, each a value that much match,
except negative numbers don't have to match.
<nodedimpnt> = 4 dimensions, each with a pointer to an integer,
to allow returning with the value of dimensions that
were not specified. A NULL means don't return that dimension.
radius = distance within which element/element must match
distfunc = distance function, normally "dist2d" or "dist3d"
rnode = node defining radius within which match can occur
The "foreach" statement allows you to access neural
elements and nodes with a partial specification of their
range. It iterates a statement or block of statements
(inside "{}") over an element type and/or set of nodes,
selected by the <nodedim> value described above. You can
select which nodes will match by giving expressions inside
square brackets (as you normally would to define a node).
For any dimension that you wish to leave free for iteration,
place a "?" directly in front of a variable's name. This
replaces the expression you would normally enter for the
dimension's value. A "within" clause specifies that
the elements or nodes must be within the specified distance
from the given node.
(interpreted:)
i = 50;
foreach node [i] ?j ?k { print j, k; };
(compiled:)
i = 50;
for (epnt=elempnt; epnt=foreach(epnt,i,-1,-1,NULL,&j,&k); epnt=epnt->next)
printf ("%d %d\n",j,k);
This statement prints the second and third dimension of
all nodes that have a value of i (= 50) in their first
dimension. The "foreach" statement in many cases is easier
to use than its equivalent nested "for" loops (one "for"
loop is normally required for each unspecified dimension).
(interpreted:)
foreach sphere ?s { if (s->dia > 5) display element s };
(compiled:)
for (epnt=elempnt; epnt=foreach(epnt,SPHERE); epnt=epnt->next)
{ s = (sphere *)epnt; if (s->dia > 5) display (epnt,1,1); }
This statement displays all spheres with a diameter greater
than 5 microns. The variable "s" specifies the element
number, and is given a new value (another sphere's element
number) for each iteration of the loop.
(interpreted:)
foreach cable ?x node [i][j] ?k {if (k>10) display element x};
(compiled:)
for (epnt=elempnt; epnt=foreach(epnt,CABLE,i,j,-1,NULL,NULL,&k); epnt=epnt->next)
{ if (k>10) display (epnt, 1,1); }
This statement displays all cables that connect to node
[i],[j] if their third dimension is greater than 10. The
variable "x" specifies the cable's element number, and the
third node dimension is specified by variable "k".
(interpreted:)
foreach cable ?x node [i][j] ?k within2d 10 node [a][b][c]
{if (k>10) display element x};
(compiled:)
for (epnt=elempnt; epnt=foreach(epnt,CABLE,i,j,-1,NULL,NULL,&k,10,dist2d,ndn(a,b,c)); epnt=epnt->next)
{ if (k>10) display (epnt, 1,1); }
This statement displays all cables that connect to node
[i],[j] if they are closer than 10 um from node [a][b][c].
The variable "x" specifies the cable's element number, and the
third node dimension is specified by variable "k". You can
specify the distance in 3D with the keyword "within3d".
Note about use of "erase" inside "foreach" statement
Example:
foreach node [i][j] ?k {
if (k > nbranches)
erase node [i][j][k]; /* Correct */
};
foreach node [i][j] ?k {
if (k > nbranches)
for (n=0; n<5; n++)
erase node [i][j][k+n]; /* Incorrect, undefined */
};
Windowing function
To "window" (cut back to within bounds) the neural elements
already created, use the "elimit" statement. You can window
all elements, in which case you should specify [-1] for all
the node dimensions, or you can select only matching elements,
similar to the "foreach" statement above. Bounds for windowing
are set by "max", and "min" values:
(interpreted:)
ymax = xmax = 100;
ymin = xmin = -100;
elimit X max xmax min xmin Y max ymax min ymin;
foreach element ?c node [-1][-1][-1] {
elimit element c;
};
(compiled:)
ymax = xmax = 100;
ymin = xmin = -100;
elimit (X, max=xmax,min=xmin); /* set bounds */
elimit (Y, max=ymax,min=ymin);
for (e=elempnt; e; e=t) { /* cut elems outside bounds */
t = e->next;
elimit (e);
}
Procedure and function definitions
Procedures and functions have a different syntax than
in "C" for their definitions, but use standard C syntax
when they are called (invoked):
proc makecell (node1, node2) { /* procedure definition */
at node1 sphere dia 10;
conn node1 to node2 cable dia 1 length 10;
};
func rms (val1, val2) { /* function definition */
return ( sqrt( val1 * val1 + val2 * val2));
};
for (i=0; i<100; i++)
val = rms (i,10); /* use of function */
printf ("%g\n", val);
};
Note that procedures and functions must be defined before
they are used, and they must be "external", i.e. they cannot
be defined from inside other procedures or functions. They may be
defined inside an 'if' statement when it contains no local
variable definitions, or when the procedure or function has no
arguments or local variables.Assigning procedures and functions
proc oldproc(s,x,y) { /* original procedure definition */
print s,"=",x+2*y+y*y;
};
proc newproc = oldproc; /* assign new procedure to old */
newproc("var",1,8);
var = 81
func oldfunc(x,y) { /* original function definition */
return log(x+2*y+y*y);
};
func newfunc = oldfunc; /* assign new function to old */
newfunc(1,8);
4.3944492
func abc = log; /* assign new function to builtin */
abc(2);
0.69314718
Exit statement
To stop a program from running, use the "exit"
statement as you would in C. This immediately stops
the execution of any more commands and exits, even
from within a procedure or function.
Macros (cpp)
#define maxmin(gain,offs) max (1-offs)*gain min (0-offs)*gain
Then, later in the script file, you can put:
plot V[1] maxmin(1e-9,0.3);
Then run the script like:
nc -C file
and the pre-processor will expand the macro to:
plot V[1] max (1-0.3)*1e-9 min (0-0.3)*1e-9;
Use of the "#define" statement allows you to redefine or shorten
the syntax that "nc" understands to simplify your scripts. The
cpp pre-processor replaces the text that calls the macro by the
macro text, with the arguments replaced by those from the call.
To see the changes that the pre-processor makes, run "cpp -P
file". Include and system commands
system ("nc --var1 23.5 file.n > file.r");
or
system ("file.n --var1 23.5 > file.r");
rseed = atof(system ("date +%m%d%H%M%S")); /* set random seed from date */
machine = ccstr(system("hostname -s")); /* get machine name, remove CRLF */
(interpreted:)
#! /home/nc/bin/nc -c
#
# script file run_multsim_1
#
/*--------------------------------------------------------*/
func runnc(randnum, lim, td)
/* function to run an nc script with different values of parameters */
/* and return its output. */
{
fmt = "nc -r %8.8g --limit %g --td %g --info 1 file.n";
sprintf (str,fmt,randnum,lim,td);
return system(str);
};
/*--------------------------------------------------------*/
proc runtest (lim, td)
/* procedure to run an nc script and return a value to an "nc" variable. */
{
for (m=i=0; i<nsim; i++) {
randum = int(rand()*1e8);
m += runnc(randnum, lim, td);
};
printf ("lim %g td %g m %-10.5g\n", lim, td, m/nsim);
};
.
.
.
(compiled:)
//
// script file run_multsim_1
//
/*--------------------------------------------------------*/
char *runnc(int randnum, double lim, double td)
/* function to run an nc script with different values of parameters */
/* and return its output. */
{
fmt = "nc -r %8d --limit %g --td %g --info 1 file.n";
sprintf (str,fmt,randnum,lim,td);
return xsystem(str);
};
/*--------------------------------------------------------*/
void runtest (double lim, double td)
/* procedure to run an nc script and return a value to an "nc" variable. */
{
int i, randnum;
double m;
for (m=i=0; i<nsim; i++) {
randum = int(rand()*1e8);
m += atof(runnc(randnum, lim, td));
};
printf ("lim %g td %g m %-10.5g\n", lim, td, m/nsim);
};
.
.
.
NeuronC Variables
Variables and arrays are "global" unless specified to be
local (see "local variables" below),
i.e. they can be accessed from anywhere
in a program once defined (in the case of variables, by
assigning a value to them). Variables and arrays must start
with alphabetic characters, but may include numbers and the
underline ("_") character. NeuronC variables are all
double-precision floating point, which means that they all
have at least 15 decimal digits of precision. NeuronC
allocates space for a variable whenever it first appears in
a program, but does not initialize the variable. You must
assign a value to a variable or array before using it, or
you will receive an error message.
Type() function
To find the type of a variable or expression, either numeric or string,
you can call the "type()" function like this:
type(<expr>);
This returns a number that describes the type of the expression. You can
compare this type number to the type of other variables or expressions.
Strings
Variables and arrays can have either numeric or string
values. Once the variable has been assigned a value, you
cannot change its type, i.e. it is an error to attempt to
store a numeric value into a string variable and vice-versa.
You can, however, assign a different value to a string
variable, and you can add two strings together using the "+"
and "+=" operators (other operators do not work on strings).
String values are assigned to a variable like this:
x = "Strings ";
y = "make ";
z = "useful labels.";
String operators
(interpreted:)
str1 + str2 catenates two strings.
str1 = str2 assigns string 2 to string 1.
str1 += str2 catenates string 2 to string 1.
Logical operators
str1 == str2 true if strings are same.
str1 != str2 true if strings are different.
str1 || str2 true if either string 1 or string 2 exist.
str1 || numval true if string 1 exists or numval is non-zero.
str1 && str2 true only if string 1 and string 2 both exist.
!str true if string does not exist.
strlen(str) returns length of string.
strtok(str1,str2) returns first substring in str1 delimited
by any of the chars in str2. The str1 string
can be parsed further by passing a 0 instead
of str1; str1 is remembered by "strtok" through
several calls. (For further information, look
in the Programmer's Reference Manual under
"string(3x)").
strcmp(str1,str2) returns 0 if strings are equal, like "strcmp(3x)"
strstr(str1,str2) returns position of str2 within str1, 0=start, -1=not found.
substr(str,i,n) returns substring of str starting at i, length n.
strchr(s1,ch) returns first char "ch" within s1, 0 = start, -1 => not found
strrchr(s1,ch) returns last char "ch" within s1, 0 = start, -1 => not found
ccstr(str) returns str with all control chars removed.
The result of a logical operator is always a numeric value,
either 1 (true) or 0 (zero=false).
print x + y + z;
Strings make useful labels.
print x + "often " + y + z;
Strings often make useful labels.
x += "used wisely ";
print x + y + z;
Strings used wisely make useful labels.
x = "";
if (x) print x
else print "empty string";
empty string
Of course, you can use the "printf" statement to format your
reports with numbers:
cablediam = 5.6;
print "The current diameter is:", cablediam;
The current diameter is: 5.6
printf ("The current diameter is: %-.3f.\n",cablediam);
The current diameter is: 5.600.
You can "add" (catenate) string and numeric variables:
w = 5;
print x+"often "+y+5+z;
Strings often make 5useful labels.
print x+"often "+y+5+" "+z;
Strings often make 5 useful labels.
print x+"often "+y+"5 "+z;
Strings often make 5 useful labels.
Setting variables from command line
Often it is useful to set a global variable to a default
value within a nc program, but to override the variable's
value from the command line. This is possible with the
predefined "setvar()" function. This function may be
invoked after the default values are set:
/* Program nfile1 */
bsize = 5;
nset = setvar(); /* nset is number of params set */
.
.
other statements that use "bsize"....
/* end of program */
Later, when the program is run, the variable
may be changed from the command line:
nc -s bsize 6 nfile1.n
or
nc --bsize 6 nfile1.n
In this case "--bsize 6" sets the variable
"bsize" to a different value after it has been set
to the default value of 5. This is useful doing
several runs of a file with different parameter
values. The "setvar()" function returns the number of
parameters that were set from the command line. If the
function is not assigned to a variable then "nc" will print
the number to "stdout" (the output file).
(compiled:)
double gctheta;
char *funcfile;
int *ntrials;
int make_cone = 1;
int make_a17 = 1;
int make_gc = 1;
void setptrs(void)
{
setptr("gctheta", &gctheta); /* register command line variables, with init */
setptr("funcfile", &funcfile);
setptr("ntrials", &ntrials);
setptrn("make_cone", &make_cone); /* register command line variables without init */
setptrn("make_a17", &make_a17);
setptrn("make_gc", &make_gc);
}
Note that in addition to registering the variable, the "setptr()"
procedure initializes the variable with a "magic" number
(LARGENUM in nc.h) that means it is "not initialized", allowing
you to use the "notinit()" function to test whether it has been
set. The "setptrn()" procedure does not initialize the value,
allowing you to set the value as a default before calling the
"setvar()" procedure at the beginning of your program.
Then, in your program, you include the following code
to initialize the simulator correctly, you call the "ncinit()"
procedure:
(compiled:)
main(int argc, char **argv)
{
ncinit(argc,argv); (initializes command-line variables, sets clock, etc.)
timinc = 1e-4;
endexp = .5;
.
. (code to set default parameters)
.
setvar();
.
. (code to construct model and experiment)
.
run();
ncexit();
}
The "ncinit()" procedure (inside "ncfuncs.cc") takes the two arguments
describing the command line (argc, argv) from "main()", calls the
"setptrs()" procedure to define the command-line variables, and sets
their values. It also sets the default simulation variables, and
sets time to zero. Setting command line variables from previously set variables
Once a numeric variable is defined in C++ code using the "setptr()" procedure,
you can set its value on the command line with eiher a numeric variable, or a
symbol, i.e. the name of another numeric variable that has already been
defined. The "setvar()" function can determine the variable's type. If the
symbol has previously been given a numeric value, its value will be transferred
into the numeric variable.
(compiled code for prog2:)
int val1;
int val2;
int www;
int xxx;
int yyy;
char *zzz;
main(int argc, char **argv)
{
ncinit(argc,argv); (initializes command-line variables, sets clock, etc.)
timinc = 1e-4;
endexp = .5;
.
. (code to set default parameters)
setptr("val1", &val1);
setptr("val2", &val2);
setptr("www", &www);
setptr("xxx", &xxx);
setptr("yyy", &yyy);
setptr("zzz", &zzz);
val2 = 6;
setvar();
.
fprintf (stderr,"www %d xxx %d yyy %d zzz %.20s\n",xxx,yyy,zzz);
.
run();
}
prog2 --val1 5 --www val1 --xxx www --yyy val2 --zzz val1
www 5 xxx 5 yyy 6 zzz val1
Click here to return to NeuronC Statements
Command line parameters inside script
When you run nc from inside a script file you can make use of
command line parameters as you would in an external script file.
To access the command line paameters, the first line of the
script file must start with "#! nc -c". This tells the shell that
runs the script to run the script file automatically with nc.
interpreted:
#! /home/nc/bin/nc -c
#
# script file "run_func"
#
. . .
Then you can run the script like this:
run_func --t1 233 --t3 422
and the variables t1 and t3 will have their values automatically
assigned from the command line.
Accessing command line parameters with argc and argv
To access the command line parameters without directly assigning
them to variables, you can use the "argc" and "argv" variables.
Thes are predefined by the "nc" interpreter to contain the number
of command line parameters (argc), and an array of the parameters
(argv), as in standard C/C++.
interpreted:
#! /home/nc/bin/nc -c
#
# script "make_types"
#
print argc, argv;
typ = argv[1];
for (f=1; f
Then:
make_types t2 morph.cell0{4[123]?,44[0-9]}
This script can then be run from other scripts.Local variables
Local variables and arrays may be defined inside a "proc" or "func"
(or a statement block) for use within that subroutine (or
block) only. This is useful when a variable of the same
name is used in a main loop and also in a subroutine, so
that the two instances of the variable may have different
values. The values are kept separate on the subroutine's
stack. It is good programming practice to use local
variables whenever possible to keep a program simple and
avoid programming errors. Local variables make it easier to
track down where in a program they are set and used. This
is how local variables are defined in NeuronC:
proc xydistance (x,y)
{
local x2,y2,rdist;
local dim power[100];
code starts here after local def...
};
Local variables can be defined at the beginning of any "{ }"
block, e.g. inside a "{ }" block inside an "if" or "for"
statement and within nested blocks. If a variable name has
been defined in several nested blocks, and referred to by a
statement enclosed in an inner block, the inner definition
is used. Note that local variables defined inside a block
are visible only to statements inside that block. Local
variables defined outside a block are also visible inside
the block (if their names are not defined more locally).
Example of nested local definitions:
{ local x1, y1;
x1 = ...
if (x1 > 5) { local x2, y2;
x2 = ...
if (x2 > x1) ... /* x1 is defined outside of inner block */
};
};
Arrays and Matrices
Arrays in NeuronC are also "double" floating point, and
are defined by the "dim" statement:
dim conearray [30][30][3];
The dimension parameters need not be constants but
may be variables or expressions:
dim rodarray [xsize] [ysize] [abs(sin(theta))];
Arrays may be assigned string values, with the same rules
as ordinary variables:
x = "first string";
dim z[10];
z[0] = x;
z[1] = "second string";
z[2] = z[0] + z[1];
print z[2];
first stringsecondstring
Arrays may be initialized when they are defined or
afterwards. There are several ways to initialize an array.
The initialized values go into memory sequentially, and
the right-most array indices increment most rapidly (as in
standard C):
dim arr1 [4][2] = {{ 1, 2, 3, 4, 5, 6, 7, 8 }};
print arr1;
1 2
3 4
5 6
7 8
print arr1 [1][1];
4
arr1 = {{ 10, 9, 8, 7 }};
print arr1;
10 9
8 7
5 6
7 8
print arr1 [1][1];
7
An array can also be initialized with an automatic
{{begin:end:step}} to denote a sequence of values:
dim arr3 [4][2]= {{0:7}};
print arr3;
0 1
2 3
4 5
6 7
But any initializations that goe beyond the dimensions
are ignored:
dim arr4 [4][2]= {{0:16}};
print arr4;
0 1
2 3
4 5
6 7
To initialize all the array contents to a single value,
place just that value in the initialization string. An
initialization can assign values to an existing array, but
the array remains at least the original size:
dim arr1[6] = {{ 0 }};
print arr1;
0 0 0 0 0 0
arr1 = {{1,2,3,4}};
print arr1;
1 2 3 4 0 0
dim arr2 [] = {{ 1, 2, 3, 4 }};
or
dim arr2 [] = {{1:4:1}}; /* {{ low : high : incr }} */
or
arr2 = {{1,2,3,4}};
or
arr2 = {{1:4}};
dim arr2 []= {{0:16:2}};
print arr2;
0 2 4 6 8 10 12 14 16
dim arr2[] = {{ 0 }};
print arr2;
0
arr2 = {{1:50000:3}};
sizeof(arr2);
16667
dim abc[5][2] = {{1,2,3,4,5,6,7,8,9,10}};
proc printx (x) {
print x;
};
proc printy(y) {
local dim z[5]= {{10,9,8,7,6}};
printx(z);
printx(z[3]);
printx(y);
printx(y[3][1]);
};
printy (abc);
10 9 8 7 6
7
1 2
3 4
5 6
7 8
9 10
8
x = "5";
dim y[] = {{5,6,7,8}};
print x+y;
10 11 12 13
print y+y;
10 12 14 16
print y*y;
25 36 49 64
print pow(y,y);
3125 46656 823543 1.677722e+07
print pow(y,y)+x;
3130 46661 823548 1.677722e+07
x = 5;
dim y[] = {{"5","6","7","8"}};
print x+y;
55 56 57 58
print y+x;
55 65 75 85
print y+y;
55 66 77 88
/*--------------------------------------------*/
dim abc[] = {{1,2,3,4,5,6,7,8,9,10}};
proc printd(d)
{
print(amax(d));
print(fmax(d,5));
print(d*2);
print(d++);
print(-d++);
print((d-9)>0);
print((4<=d && d<=9)*d);
print(amax(d));
};
printd(abc);
10
5 5 5 5 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20
1 2 3 4 5 6 7 8 9 10
-2 -3 -4 -5 -6 -7 -8 -9 -10 -11
0 0 0 0 0 0 0 0 1 1
0 4 5 6 7 8 9 0 0 0
12
/*--------------------------------------------*/
dim a[] = {{"Is", "this", "a", "match","?"}};
dim b[] = {{"Yes", "it's a", "good", "maker", "!"}};
g=(a=="match");
h=(b!="maker");
print a,b;
print g;
print h;
print (a*h + b*g);
print (a*g + b*h);
Is this a match ? Yes it's a good maker !
0 0 0 1 0
1 1 1 0 1
Is this a maker ?
Yes it's a good match !
dim c[] = {{"Must", "be", "a", "match","."}};
print "Found", (c==a)*c;
Found a match
/*--------------------------------------------*/
Matrix operations
x = a + b matrix add
x = a - b matrix subtract
x = a * b matrix scalar multiply
x = a / b matrix scalar divide
x = matmul(m1,m2) matrix multiply
x = transpose(m) matrix transpose
x = matinv(m) matrix invert
x = matsolve(A,b) solve A * x = b
Array dimensions
dim oldarr[5][3][1];
adim = dims(oldarr);
print adim;
5 3 1
print sizeof(adim);
3
proc initarr (arr,val) {
/* procedure to set an array to a value */
local i,j,k,ndim;
adim = dims(arr); /* get dimensions of array */
ndim = sizeof(adim); /* find how many dimensions */
if (ndim==1) {
for (i=0; i<adim[0]; i++) {
arr[i] = val;
};
}
else if (ndim==2) {
for (i=0; i<adim[0]; i++) {
for (j=0; j<adim[1]; j++) {
arr[i][j] = val;
};
};
}
else if (ndim==3) {
for (i=0; i<adim[0]; i++) {
for (j=0; j<adim[1]; j++) {
for (k=0; k<adim[2]; k++) {
arr[i][j][k] = val;
};
};
};
};
print arr;
};
initarr(abc,0); /* set the array to all zeroes */
Arrays can be erased with the "erase" statement:
erase rodarray;
Array size is limited only by the hardware and "C" compiler.
Array access time is slower than simple variable access time
because the array indices must be multiplied by the dimension
sizes to locate a value in the array.Local arrays
Arrays may be defined inside any procedure, function, or
statement block in a manner similar to local variables.
They may have numeric or string values. The "dim" keyword
must be used for each definition:
{ local dim x[100], dim y[100];
local i,j, z[100][100];
local mcond;
local dim cond[mcond=calcval(120)];
z[i][j] = x[i] + y[j] * cond[i+j];
...
};
The dimension of a local array must be an expression whose
value is known at the time its definition is encountered by the
interpreter. As in the example above, the dimension can be a
constant, or can be calculated by a function or be the result of
an assignment. Except for such assigments, the local definitions
must be made before any other statements in the code block. Local
arrays can be initialized in the "dim" statement or afterwards
(see "Arrays" above"). NeuronC Arithmetic Operators:
NeuronC has many of the unary and binary operators that
are familiar to users of C. Remember, in logical
expresssions, NeuronC (as other languages) considers a value
of 0 to be "false" and nonzero to be "true". Logical
comparison operators return 1 when true and 0 when false.
unary operators
- negative
! logical NOT (!x true when x==0)
x++ post-increment (add one to value after use)
x-- post-decrement (subtract one after use)
++x pre-increment (add one to value before use)
--x pre-decrement (subtract one before use)
binary operators
+ addition
- subtraction
* multiplication
/ division
% modulo (as in C/C++)
^ power (A^B == A to the power of B)
& bitwise AND (x&1 true when x is odd)
| bitwise OR (y|1 sets ones bit in y)
^^ bitwise XOR (y^^1 inverts ones bit in y)
&& logical AND ("x && y" true if both x and y nonzero)
|| logical OR ("x || y" true if either x or y nonzero)
comparison operators return value of 1 if true or 0 if false
> greater than
>= greater than or equal to
< less than
<= less than or equal to
== test for equal to (no assignment of value)
!= not equal to
assignment operators
= assignment
+= increment by right hand side (x+=2: add 2 to x).
-= decrement by right hand side (x-=2: subtr 2 from x).
*= multiply by right hand side.
/= divide by right hand side.
NeuronC keywords:
Keywords have special meanings in NeuronC. You
should not use any of these words as names for
variables because this will cause an error.
The keywords are:
abs acos acov allowrev amax amin ampa area asin at atan
atan2 atof attf backgr bar batt bic binomdev blur break
btot btoti
cAMP cGMP cable cabuf cabufb cacolor cacomp caexch
cahc cai cakd calcnernst calibline camp cao cap caperm
capump cbound cclamp ccstr center cgain cgmp chan char
chc checkerboard chinf chnoise chset chtau cinf ckd
close cm cmap cnqx coff color complam comps cone conn
connect continue contrast copychan cos cplam crit cshell
ctau ctaua ctaub ctauc ctaud ctaue ctauf d1 d2 dampau
darknoise dash dbasetc dbasetca dbasetdc dbasetsyn dbd1
dbd2 dbk1 dbk2 dcabf dcabnd dcabr dcabt dcabti dcadens
dcahc dcai dcakd dcakex dcalu dcao dcaoffs dcapkm dcashell
dcaspvrev dcatauf dcatauh dcataum dcatu dcavmax dcavoff
dcgmpu dchc dckd dsclcac dclcavs dclcavsc dclcasu
dcli dclo dcm dcoo ddca debug
debugf debugz delay deleccap density dfta dftah dftb
dgjnv dgjoff dgjtau dia dia1 dia2 dim dims dinf diode
disp display djnoise dkau dkcabu dkcasu dkcatauh
dkcataum dkdens dki dkihu dko dkoffsh dkoffsn dkrseed
dktauf dktauh dktaum dku dmaxampa dmaxca dmaxclca
dmaxcon dmaxgaba dmaxk dmaxna dmaxnmda dmaxrod dmaxsyn
dmgo dnadens dnai dnao dnaoffsh dnaoffsm dnatauf dnatauh
dnataum dnau dnmdamg dpcaampa dpcacgmp dpcak dpcana dpcanmda
dpcasyn2 dpkca dpkna dpnaca dpnak dqc dqca dqcab dqcavmax
dqcrec dqd dqdc dqeff dqh dqkca dqm dqn dqna dqnb dqrec
dqri dqrm dqsyn dratehhh dratehhm dratehhna dratehhnb drg
dri drift drm drs dsc dscale dscavg dscu dsd1 dsd2 dsfa
dsfb dsg dshc dsintinc dsintres dsk1 dsk2 dskd dsms dsmsgc
dsn dsrrp dst dstr dsvn dsyntau dsyntauf dtau dtcai dur
dvg dvsz dyad
e2dist e3dist edist edit efrac elabl elap_time electrode
element elimit else ename endexp erase euler except exist
exit exp exp10 expon ezdist
fclose fft fgetc fgets file filt fmax fmin fopen for foreach
fprintf fputc fread fscanf func fwrite
gaba gabor gamdev gasdev gausnn gauss gcirc gcrot gcwidth
gdash gdraw getflds getpid gframe ginfo gj glu gly gmax gmove
gndbatt gndcap gnv gorigin gpen gpurge graph grdraw grect
grmove grot gsize gtext glabel gvpen gwindow
hcof hgain hide hinf htau
if ifft implfk implicit include infile info init initrand
int inten jnoise
k1 k2 kd kex km
label lamcrit lcolor length linear linit lmfit lmfit2d load
loc local log log10 loopg
makestim mask matching matinv matmul matsolve max maxcond
maxsrate mesgconc mesgin mesgout mg min minf model modify
mtau n2dist
n3dist nacolor ncomps ncversion ndensity ndist
newpage nfilt1 nfilt1h nfilt2 nfilt3 ninf nmda nnd nnstd node
node1a node1b node1c node1d node2a node2b node2c node2d
notinit nozerochan nstate ntau ntype numconn numdyad numsyn
nzdist
offset offseth offsetm oldsynapz only opamp open orient
pathl pen pfft photnoise phrseed pigm plmax plmin plname plnum
plot ploti plsep plsize plval plarr poisdev pow print print_version
printf printsym prmap proc progname ptx puff put
radius rand range rcolor read rect refr reg relax relincr
resistor resp restart restore return rev rg rgasdev ri rightyax
rm rmove rod rrand rrpool rs rsd rseed run
save scanf scatter scurve sdyad sens set_q10s setchan_cond
setchan_mul setchan_ntrans setchan_rateo setchan_trans
setchan_trate setvar setxmax setxmin setymax setymin sgcolor
silent simage simwait sin sine sineann size sizeof sphase
sphere spost spot sprintf sqrt srcolor srseed sscale sscanf
start stderr stdin stdout step stim stim_elem stimelem
stiminc stimonh stimonl strcmp strlen strstr strtok stry
stype substr sun syn2 synapse synaptau system system_speed
tan tau taua taub tauc taud taue tauf tauh taum taun tcai
tempcel tfall2 tfall3 tfreq thresh time timec1 timec1h timec2
timec3 timinc to transducer transf transpose trconc tungsten
type
unit unlink unmaskthr unmaskthr2
varchr varnum varstr vbuf vcl vclamp vcolor vcov version
vesnoise vgain vidmode vk vmax vna vpen vrest vrev vsize
wavel while width windmill window within2d within3d
xenon xenv xloc xrot
yenv yloc yrot
zloc zrot
ACH AMPA BIC CNQX Ca Char ClCa CoV DEG E
FA0 FA1 FA2 FA3 FA4 FA9 FB0 FB1 FB2 FB3 FB4
FC0 FC1 FC2 FC3 FC4 FC9 FH0 FH1 FH2 FH3 FH4
G G0 G1 G2 GABA GAMMA GLU GLY Gabor
H I IE IP IPE Im K KCa L M N NMDA Na
PHI PI PTX S STRY UNINIT V X Y Z
To track down these keywords, look in "nc/src/init.cc" and from there
look in "nc.y" to understand the details of their usage (if this manual
doesn't describe them well enough for you). You can print out all the
keywords into a sorted list with the commands
nc -K | sort.
nc -K | sort | less
nc -K | sort > file
Read input into variable
read
This function reads a value from the keyboard (standard
input) into a variable. It returns 1 if a variable was
read, or 0 if not. Typical usage:
while (read(x)) print "Value is:",x;
Note that the familiar "scanf()" statement also exists in NeuronC
(see "scanf function" below).
File open and close
fd = fopen (filename,mode)
fclose (fd)
The "fopen" statement opens a file, given its name and a mode
("r" = read, "w" = write, "a" = append), exactly as in standard
C. It returns a file descriptor which may be used by file
read and write statements to refer to the file. The file
descriptor is a standard number with a special value. If the
file could not be opened, the returned file descriptor is
zero. To test for this you can write code like this:
filnam = "test.n";
filmode = "r";
/* to generate an error if file is not found */
if (ftemp=fopen(filnam,filmode)) == 0) {
fprintf (stderr,"fopen: can't open file '%s'.\n",filnam);
exit;
};
/* to try something else if file is not found */
if (ftemp=fopen(filnam,filmode)) > 0) {
/* file was found */
...
}
/* same thing, testing for non-zero */
if (ftemp=fopen(filnam,filmode)) {
/* file was found */
...
}
The "fclose" statement closes a file given its file
descriptor.Printf statements
print <expr> <expr>
printf ("format", <expr> ...
fprintf (file,"format", <expr> ...)
sprintf (stringvar,"format", <expr> ...)
The "print" statement prints the value of any expression,
or list of expressions. The expression may have either a
number or string value. A comma-separated list of
expressions is printed with spaces separating the values.Scanf function
n = scanf("format", <var> ...)
n = sscanf(stringvar,"format", <var> ...)
n = fscanf(<fd>,"format", <var> ...)
n = fgets(<var>,<n>,<fd>)
n = fgetc(<var>,<fd>)
n = fputc(<var>,<fd>)
n = getflds(<fd>)
The "scanf()" function is identical to the familiar library
function "scanf()". It reads a formatted string from the
"standard input". It requires a "format" string, which may
contain literal characters and formats of numbers or strings to
be printed. A number format has a "%" followed by "lg" (double),
and a string has "%s". "scanf()" returns the number of
arguments converted.
fd = fopen (argv[i],"r");
dim Fld[] = {{"x"}};
for (flds=0; Fld = getflds(fd), flds=sizeof(Fld) > 0; flds=flds) {
if (Fld[1] == "#") { // comment line
print Fld[0];
}
else {
x = atof(Fld[1]); // get numeric value from first token
y = atof(Fld[2]);
...
};
...
};
Click here to return to NeuronC Statements
Fread statement
interpreted:
fread ( <filename>, <arrname>, <var>, [<var>] )
freads ( <filename>, <arrname>, <var>, [<var>] )
compiled:
double *fread ( <filename>, <var>, <var> )
char **freads ( <filename>, <var>, <var> )
char **freads ( <filename>, <var>, <var>, <var> )
where:
<filename> = name of file that contains numerical array
(can be "string" or string variable).
<arrname> = name of array (not yet defined).
<var> = variable to contain dimension size of array.
[<var>] = optional variable for second dimension size.
The fread statement reads a file of numbers (or variables)
into an array of one or two dimensions. The file contains a
list of numbers separated by spaces. The array must not yet
be defined, because the statement defines the array to match
the dimension(s) of the list of numbers in the file. The
(one or optionally 2) var's are set to the sizes of the
array's dimensions. The size of the first dimension is the
number of lines (with numbers on them) in the file, and the
size of the second dimension is the number of numbers on the
first line. The freads statement is similar but reads a file
of strings, and does not interpret them as numbersVariables in file array
The "fread" file may contain a mixture of variables
along with numbers. The variables are treated in the
same way as the numbers, except that after they are
read, their values from the symbol table are
substituted. Therefore, any variables occurring in the
file must be assigned a value before the "fread" statement.
The definition may be:
1) in an assignment statement: x = 87
or 2) in a command line assignment: nc -s x 87
Expressions in file array
When the variable "fread_expr" is set to 1 (default 0)
the file read by fread may contain expressions. However,
in this case the expressions may not contain spaces. The
expressions may contain any numerical variables or functions
as long as they are defined before the file is read.
Examples:
4*3 4*2 4*diam 4*6 (mult OK, no spaces)
size+2 size-3 size*4 size/5 (where size is predefined)
log(2*x) log(3*x) log(4*x) log(5*x) (where x is predefined)
Freads statement
interpreted:
freads ( <filename>, <arrname>, <var>, [<var>] )
compiled:
char **freads ( <filename>, <var>, <var> )
char **freads ( <filename>, <var>, <var>, <var> )
The freads statement is similar to the fread statment except
that it reads string values from a file of 1 or 2 dimensions
and creates an array of string type. It does not intepret the
strings as numbers or expressions. Its delimiters that define
the separate string values are by default: [ ,:\t\n\r]. To set
the delimiter chars (e.g. comma and semicolon), you can include
them in a string in the call to freads:
data_array = freads ( "filename", &nrows, &ncols, ",;" );
Fwrite function
fwrite ( <filename>, <arrname>)
where:
<filename> = name of file (can be "string" or string variable).
<arrname> = name of array.
This statement writes an array of one or two dimensions
to a file. Unlink function
unlink ( <filename>)
where:
<filename> = name of file to remove (can be "string" or string variable).
This statement removes a file. Access to variables from an external program
You can compile "nc" into your own C program, call it as a
subroutine, and return results from the simulator back to your
program as memory references. To do this, read through
"src/nctest.cc" which is a template for how to access internal
"nc" variables from the outside. Edit "src/ncmain.cc" and rename
"main()" to "ncmain()", then use the "nctest" lines in the
src/makefile as a template for compiling and linking your C own
program. You can run the simulator several times with parameters
set to different values and return the results in variables or
multidimensional arrays.Test for variable definitions: notinit(), varnum()...
When variables are first declared, they have an undefined value,
which is useful when debugging a script. The "notinit()"
function allows one to test whether a variable has been assigned
a value. It returns a 1 ("true") when its argument has not been
intialized yet, and a 0 ("false") when it has been initialized.
This is useful to find under what circumstances a variable is
assigned a value.
if (notinit(<var1>)) var1 = 100; /* set a default value */
if (notinit(<var1>)) fprintf (stderr,"Error in defining var1, %g\n", <var2>);
if (varnum(<var1>)) printf ("var is a number\n");
if (varstr(<var1>)) printf ("var is a str\n");
if (varchr(<var1>)) printf ("var is a char\n");
Run procedure at plot time
Sometimes it is useful to do something else besides directly
printing out a value at plot time. For example, one might want
to perform some operation on the voltages or currents recorded
from a neuron before plotting them.
(interpreted:)
func calctau (tau)
/* Function to calculate "k" for digital filter, */
/* given time constant. */
{
k = 1.0 - exp (-timinc/tau);
return k;
};
kf11 = calctau(1.5e-5); /* filter time constants */
kf12 = calctau(2e-5);
graph X max endexp min 0;
graph Y max 0 min 1e-10;
graph Y max 0 min 1e-10;
graph init;
proc onplot()
/* plot procedure that implements 2nd order digital filter */
{
graph pen (2,4); /* plots green, red */
val = I[1]
f11 += (val - f11) * kf11; /* second-order filter */
f12 += (f11 - f12) * kf12;
graph (time, val, f12);
};
(compiled:)
double calctau (double tau)
/* Function to calculate "k" for digital filter, */
/* given time constant. */
{
k = 1.0 - exp (-timinc/tau);
return k;
};
kf11 = calctau(1.5e-5); /* filter time constants */
kf12 = calctau(2e-5);
graph_x (max=endexp,min=0);
graph_y (max=0,min=1e-10);
graph_y (max=0,min=1e-10);
graph_init();
void onplot(void)
/* plot procedure that implements 2nd order digital filter */
{
graph_pen (2,4); /* plots green, red */
val = I[1]
f11 += (val - f11) * kf11; /* second-order filter */
f12 += (f11 - f12) * kf12;
graph (time, val, f12);
}
.
.
.
setonplot (onplot); /* set "onplot()" to run at plot time */
Click here to return to NeuronC Statements
Built-in functions
These functions return values in exactly the same way as they
do in standard "C".
(interpreted:)
x = exp(a) exponential to base e
x = exp10(a) exponential to base 10
x = log(a) natural logarithm
x = log10(a) logarithm to base 10
x = pow(a,b) power (a to the b power) = a^b
x = sin(a) sine
a = asin(x) arcsine
x = cos(a) cosine
x = tan(a) tan
a = atan(x) arctan
x = factorial(n) factorial function, a!, returns (n*(n-1)*(n-2) ... (n-(n-2))).
x = gauss(x,r) Gaussian function
x = sqrt(a) square root
x = int(a) integer value of (a)
x = abs(a) absolute value of (a)
x = amax(a,b) maximum of (a,b), single number max of array a
x = amin(a,b) minimum of (a,b), single number min of array a
x = fmax(a,b) maximum of (a,b), array or scalar values
x = fmin(a,b) minimum of (a,b), array or scalar values
x = atof(s) ascii string to number conversion
x = strlen(s) string length (s must have a string value)
x = strtok(s1,s2) returns first substring in s1 delimited
by any of the chars in s2. The str1 string
can be parsed further by passing a 0 instead
of s1; s1 is remembered by "strtok" through
several calls. (For further information, look
in the Programmer's Reference Manual under
"string(3x)").
x = strcmp(s1,s2) returns 0 if strings are equal, like "strcmp(3x)".
x = strstr(s1,s2) returns position of s2 within s1, 0 = start, -1 => not found
x = strchr(s1,ch) returns first occurence of char "ch" within s1, 0 = start, -1 => not found
x = strrchr(s1,ch) returns last occurence of char "ch" within s1, 0 = start, -1 => not found
s = substr(s,i,n) returns substring of s starting at i, length n.
s = ccstr(s) returns s with all control chars removed.
x = isnum(s) returns 1 if s is numeric, otherwise 0.
x = system_speed() system CPU speed (approx, in MHz).
x = wait(nsecs) wait specified time (seconds).
x = elap_time() elapsed computation time (minutes).
x = getpid() process number, useful to make temporary file names
x = setvar() set variables specified on command line.
x = print_version() print NeuronC version.
x = printsym() print all defined symbols (keywords, variables, functions).
(same as "nc -K")
x = matmul(m1,m2) matrix multiply
x = transpose(m) matrix transpose
x = matinv(m) matrix invert
x = matsolve(A,b) solve A * x = b
x = rand() random function.
x = rrand(n) random function from individual random noise generator.
x = gasdev() Gaussian distribution with variance of 1.
x = rgasdev(n) Gaussian distribution from individual random noise generator.
x = poisdev(m) Poisson distribution, m = mean.
x = gamdev(n) Gamma interval distribution, n = order (an integer).
x = ttest(data,n) Student's independent (2-sample) t-test function; data is 2d array with 2 columns
x = ttest2(data,n) Paired t-test function; data is a 2d array with 2 columns
x = pvalue(t,df) One-sided p-value function, (t=tscore, int(df=n-1)
initrand (n) set up and initialize individual random noise generator.
initrand (n) rsd=x set up random noise generator and initialize with seed.
(compiled:)
(see math funcs defined in
elapsed_time = elap_time() /* elapsed computation time (minutes) */
estimated_time = total_measured_time * elapsed_time / measured_elapsed_time;
cpuspeed = system_speed() system CPU speed (approx, in MHz)
estimated_time = measured_time * actual CPU speed / cpuspeed;
pid = getpid() process number for simulator
Use this function to make a temporary file name:
sprintf (str,"file%06g",getpid()); # to add pid to file name
save model (str); # creates "file024994"
or
sprintf (str,"file%04g%06g",int(rand()*10000),getpid()); # to add rand num, pid
save model (str); # creates "file3032024994", pid = 024994
.
.
.
restore model (str); # restores model to original state
The first case shows how to add a 6-digit number onto the file name to make it
unique to that process, so that the code can be run by several simultaneous
simulator processes without conflict. The process number returned by getpid()
is the same as the "PID" number displayed by the "ps" command.
x = setvar() set variables designated on command line,
returns number of variables set.
The "setvar" function is useful for running a "nc"
program with different sets of parameters. Using the "-s"
commaend line switch you can set the value of any variables
for the script. The variables set by the "-s" switch need
not be already defined in the program. Normally the values
defined by the "-s" option are set at the beginning of the
nc program. However the "setvar()" function also sets the
values that you defined on the command line with "-s".
Since you can locate the "setvar()" function anywhere, it is
convenient when initializing variables for use as default
parameters. You merely run "setvar()" once after the default
values for variables have been set. This allows you from the
command line to override the default parameter values. (see
"NeuronC Variables").
This is especially useful when running "nc" from a
shell script file.
gamdev(gorder) / gorder
Testing the random number generator
glibc2 (several sizes, small and fast, or large and hi-quality
taus2 (12 bytes, good length period (2^88, 10^26), fastest in GSL)
taus113 (16 bytes, longer period than taus2 (2^113), only ~2% slower)
taus258 (40 bytes, longer period than taus113 (2^258), only ~10% slower)
tinymt (tiny mersenne twister, 32 bytes, period 2^127, many sequences, 40% slower)
mt (mersenne twister, longest random period in GSL, fast, only 10% slower)
See http://www.gnu.org/software/gsl for more on these random number generators.
The "glibc2" generator can be configured with random states of
several sizes. The smaller sizes (8, 32 bytes) are very fast but
the random sequences have significant correlations. The larger
sizes (128, 256) are still very fast and generate sequences of
very high quality. The size of 128 is set by default.
Setting the random sequence generator
To change the random sequence generator, you can edit "nc/src/drand.cc" to
comment out the existing generator and uncomment the one you want to use. Then
you also need to edit "nc/src/ncomp.h" to change RNDSIZ to the appropriate
definition for the random sequence generator that you have set in drand.cc.
Since all of the random sequence generators are included in the make file link
list, you don't need to change the makefile. Then do "make clean", and "make".
rndtest
You can test the quality of the random noise generators included
with "nc" using "diehard" which is a standard random sequence
tester (in nc/testing/diehard). You can compile "rndtest" which
is a short program included in "nc/src" and "nc/testing/diehard".
It generates a 10 MB file of binary numbers, suitable for use
with "diehard". First, go to the diehard folder (cd
nc/testing/diehard), uncomment the appropriate functions at the
top of "rndtest.cc", then compile rndtest with "make rndtest",
then run "rndtest > rnd.dat" to make a file of random numbers.
Then extract diehard with "tar xvzf die.c.tgz", then "cd
die.c", compile diehard with "make diehard". Then run "diehard"
and give the random file name that you created. "diehard" has
15 tests and you can enter a number to run one of them or a
negative number to run all but one. For each test, it runs
several tests and prints out the results. If the "p" values
are near 0 or 1 for several tests there may be correlations.
Unfortunately "diehard" crashes if test 9 (Parking Lot Test) is
run along with all the others, so you can run the tests
individually or select all except the parking lot test (enter
-9). Gausnn
(intepreted:)
n = gausnn (array, <option1,option2,...>);
where:
array = Name of array to hold the points.
Array should not be previously defined.
optional parameters: default: meaning:
--------------------------------------------------------
N = <expr> Number of cells in the array.
density = <expr> Density of cells in the array (N/um2).
nnd = <expr> 20 Mean nearest-neighbor distance (um).
nnstd = <expr> Standard deviation of nnd.
reg = <expr> 5 Regularity of the array: mean/stdev.
rsd = <expr> set by rseed Random seed for separate sequence.
center = <expr> (0,0) Location of center of array (um).
size = <expr> (200,200) Size of square array's side (um).
(compiled:)
gausnn (xarr, yarr, ncells, density, rsd, reg, xcent, ycent, ginfo);
gausnn (xarr, yarr, density, rsd, reg, xsize, ysize, xcent, ycent, ginfo);
gausnn (xarr, yarr, ncells, rsd, reg, xsize, ysize, xcent, ycent, ginfo);
gausnn (xarr, yarr, nnd, reg, rsd, xsize, ysize, xcent, ycent, ginfo);
Where:
xarr, yarr (double) x,y location of cells generated.
xsize, ysize (double) size of array (norm. in microns).
xcent, ycent (double) center of array (norm. in microns, default; 0,0).
density (double) density of cells specified.
nnd (double) nearest-neighbor distance specified.
reg (double) regularity (nnd/stdev) of cells specified.
ncells (int) number of cells specified.
rsd (int) random seed specified for the array of cells.
ginfo (int) info variable, sets level of debugging printout.
echo "x=gausnn(arr,N=1000);print arr;" | nc -r -1 -q | plotmod -C . | vid
Click here to return to NeuronC Statements
FFT
(interpreted:)
fft (array) (amplitude, phase) spectrum
ifft (array) inverse transform (amplitude, phase)
pfft (array) power spectrum
acov (array) autocovariance
dim array [2][arraysize];
(compiled:)
void fft(double *real, double *imag, int asiz, int param)
Where:
param = type of transformation: FFT, IFFT, PFFT, ACOV.
These functions compute the fast Fourier transform
of the array and leave the answer in the same
array, which must be defined with two dimensions. The
first subarray (array[0][arraysize]) dimension is
amplitude, and the second is phase (array[1][arraysize]).
Click here to return to NeuronC Statements
lmfit
The lmfit() procedure performs a Levenberg-Marquardt
least-squares fit of a function you define to an array of data
you provide.
lmfit (fit_func,data,p);
compiled:
void do_lmfit (double (*user_func) (double user_x_point, double *coeff),
int m_dat, double *xydata, int n_p, double *coeff, double *coeffc);
/* xydata array must be: arr[2][length]; arr[0] is x, and arr[1] is y.
The coeff array must be: coeff[n_p], which is starting value of
the coefficients for the function. The coeffc array contains
constraints L0, U0, L1, U1, .... 2n_p. If coeffc is NULL no constraints
are set.
*/
(interpreted example:)
dim data[2][15] = {{
.07, .13, .19, .26, .32, .38, .44, .51,
.57, .63, .69, .76, .82, .88, .94,
.24, .35, .43, .49, .55, .61, .66, .71,
.75, .79, .83, .87, .90, .94, .97
}};
dim p[] = {{1,1,1}}; // use any starting value except {{ 0,0,0 }};
func fit_func(x, p)
{
return (p[0] * x + (1 - p[0] + p[1] + p[2]) * x * x) /
(1 + p[1] * x + p[2] * x * x);
};
lmfit (fit_func,data,p);
print p;
(compiled example:)
#include
Running this example produces this output:
status: success (f) after 42 evaluations
6.259145 16.1219 6.751548
You can set constraints in your "fit_func()" by including
a test inside your function. The initial values of the
coefficients must be within the range of the constraints:
func fit_func(x, p)
{
if (p[0] < 1) p[0] = 1;
if (p[0] > 5) p[0] = 5;
return (p[0] * x + (1 - p[0] + p[1] + p[2]) * x * x) /
(1 + p[1] * x + p[2] * x * x);
};
Running this example produces this output:
status: success (f) after 60 evaluations
5 9.531072 2.152715
You can control the level of information in the lmfit
printout using the "info" variable. The default level is
"info = 2", which prints out the coefficients at every
iteration of lmfit. A setting of "info = 1" prints
out just the final message containing the number of
iterations. A setting of "info = 0" prints nothing:
nc --info 0 lm_test.n
6.259145 16.1219 6.751548
lmfit2d
kc center amplitude
rc center radius
ks surround amplitude
rs surround radius
xo X offset
yo Y offset
You may also set constraints using the parameters:
kc_max, kc_min
rc_max, rc_min
ks_max, ks_min
rs_max, rs_min
xo_max, xo_min
yo_max, yo_min
Several other parameters help in defining the fit:
file filename for square array of z values to be fit
dx delta x,y for the array
datasize size of one side of the square array
A standalone version of gaussfit called "gaussfitn.cc" is provided
that does not require linking with "libnc.a". Also provided is a
useful program to generate test Gaussian arrays is "makgauss.cc".
Constants
The following constants are defined in NeuronC:
PI 3.141592653589793
E 2.71828182845903523536
DEG 57.29577951308232
Graphics statements
gmove (x,y)
gdraw (x,y)
grmove (dx,dy) ( relative move )
grdraw (dx,dy) ( relative draw )
gcirc (rad, fill) ( fill = 0 or 1 )
grect (x1,y1,x2,y2,x3,y3,x4,y4, fill) (4 (x,y) corners, fill = 0-1 )
gpen (color) ( color range: 1-15 )
grot (theta) ( rotate picture, angle in degrees )
gcrot (theta) ( rotate text, angle in degrees )
gcwidth(width) ( character width )
gsize (size) ( size that square screen frame represents )
gdash (dashcode) ( code range 1->8 )
gorigin (x,y) ( origin of new frame in parent's coords )
gframe ("<name>") ( make new sub-frame )
grframe ("<name>") ( remove sub-frame )
gtext ("<char string>")
glabel ("<char string>", color, x, y) (draws label with color at x,y )
These graphics primitives allow NeuronC to draw to the
graphics screen, defined as by coordinates (0,0) to (1.0, 1.0).
gmove and gdraw together with gpen allow you to draw a line
anywhere in any color (16 colors for VGA). gtext writes text on
the graphics screen, in a manner similar to "printf", or you can
call it with a string and no other arguments. glabel calls
gtext(), gpen(), and gmove(). The string cannot have arguments
that would be allowed in gtext(). gcwidth sets the character
size as a fraction of the frame, i.e. .02 sets the char size to
1/50th of the frame size. grmove and grdraw are relative move
and draw. grot (calib in degrees) rotates the graphics frame
defined by gframe so graphics and text can be written at any
angle. gorigin translates the current frame. Arranging graphs
It is possible to combine these graphics primitives with
the standard "graph" and "plot" statements to arrange
several graphs on a page. For instance, you can create a
subframe with frame, translate it with gorigin, shrink it
with gsize and then draw a graph in it. After the graph is
done, you can go back to the parent frame with gframe ".."
and make another subframe for a second graph.
gframe "graph1";
gorigin (.2,.2);
gsize (.4);
code to draw points on graph
.
.
.
gframe "..";
gframe "graph2";
gorigin (.2 .6);
. . .
gframe "..";
(at this point, you can go back to either "graph1"
or "graph2" and draw more in them.)
Ttest function
To establish statistical significance between 2 sets of numbers, you can run a
ttest. If the numbers are independent between the first and second set, you
can run "ttest()". If the numbers are paired between the first and second set,
you can run ttest2(); These functions calculate the "t-score" which is a
measure of how far from the mean of the probability that the null hypothesis
(the 2 means in the original distribution are the same) is correct.
fread ("file1",data,nrows,ncols); // ncols must be 2
ttest2(data);
9.160968
ttest(data);
5.9684852
(compiled:)
double ttest(double *array, int nrows); // array is a 2d array with 2 cols and nrows
double ttest2(double *array, int nrows);
ttest2(data,nrows);
9.160968
ttest(data,nrows);
5.9684852
Pvalue function
To find the probability that the null hypothesis is true,
you can run the "pvalue()" function. Its 2 parameters are
the t-score, and the "degrees of freedom" (i.e. n-1: one less than
the number of rows in the original data).
fread ("file1",data,nrows,ncols); // ncols must be 2
ttest2(data);
9.160968
pvalue(ttest2(data),nrows-1);
2.3179505e-10
(compiled:)
double ttest2(double *array, int nrows); // array is a 2d array with 2 cols and nrows
double pvalue(double tscore, int df);
ttest2(data,nrows);
9.160968
pvalue(ttest2(data),nrows-1);
2.3179505e-10
Click here to return to NeuronC Statements
ttest.n script
To run the ttest() and pvalue() functions together, you can run "ttest.n". This is a nc script (in nc/bin) that runs in interpreted mode to run ttest2(), generating a tscore, then running pvalue() to generate a p-value probability. The ttest.n script can read a .txt file with 2 columns of numbers to be compared, or it can accept a list of 2 columns of numbers from its standard input. You can also set the t-score to see the resulting p-value. Note that this pvalue calculation gives a "one-tailed" value. For a "two-tailed" p-value, multiply the p-value by 2.
usage: ttest.n --fname filename --test 2 --> "y.yy" (do paired t-test )
or: ttest.n --fname filename --> "y.yy" (default is "--test 2" )
or: ttest.n --fname filename --f 1 --> "filename y.yy"
or: ttest.n --fname filename --flabel fil --> "fil y.yy"
or: ttest.n --fname filename --h 1 --> "paired tscore x.xx df n pvalue y.yy"
or: ttest.n --fname filename --h 1 --f 1 --> "filename paired tscore x.xx pvalue y.yy"
or: ttest.n --set_tscore z.zz --set_nrows r --h 1 --> "paired tscore z.zz df n pvalue y.yy"
or: cat filename | ttest.n --test 2 --> "y.yy"
or: cat filename | ttest.n --test 1 --h 1 --> "indep tscore x.xx df n pvalue y.yy"
or: cat filename | ttest.n --test 2 --h 1 --> "paired tscore x.xx df n pvalue y.yy"
or: cat filename | ttest.n --h 1 --flabel fil --> "fil paired tscore x.xx df n pvalue y.yy"
or: cat filename | ttest.n --test 2 --flabel fil --> "fil y.yy"
switches:
--f 1 print filename
--h 1 print 'indep' or 'paired' followed by "tscore x.xx pvalue y.yy'
--fname ddd use "ddd" as input file
--flabel zzz print flabel (i.e. instead of filename)
--ttest 1 do independent t-test (i.e. two-sample test)
--ttest 2 do paired t-test (i.e. one-sample test on the differences) (default)
--set_tscore n set a tscore instead of performing the t-test on the input list
--set_nrows n set the number of observations instead of using the input list
Click here to return to NeuronC Statements