The Moon Illusion.
A literature thesis by Bart Borghuis.
Introduction
The moon seen close to the horizon appears to be quite a bit larger than when it is viewed at its zenith. The same effect can be observed when viewing the sun or constellations of stars. This odd phenomenon is called the 'Moon Illusion' and has been studied for centuries; it was first mentioned in cuneiform inscriptions on clay tablets from the royal library at Nineveh in the 7th century BC and later recognized by Ptolemy, ca 150 AD. The first important step towards an explanation of this ancient phenomenon is establishing that what we are dealing with here is a perceptual illusion.

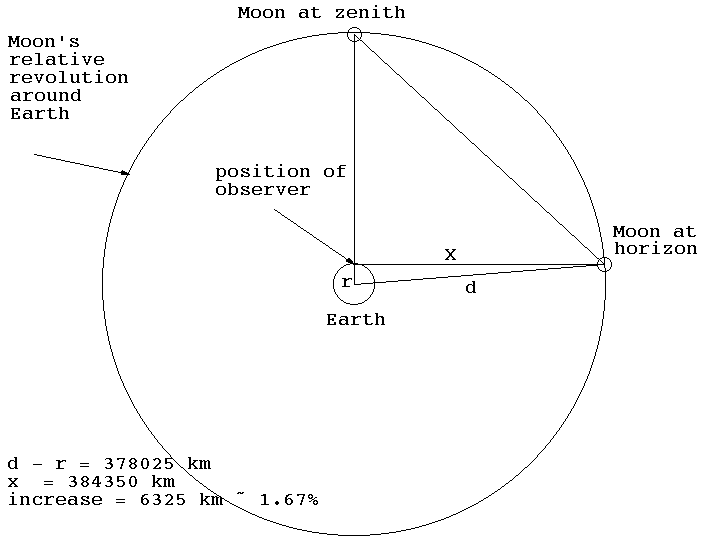
Fig. 1. The moon's orbit around Earth.
Through the ages, many writers have speculated that the illusion has a physical basis. It was suggested that the horizon moon really ís closer to the observer, and therefore seen larger, until Newton’s description of the nature of the moon’s orbit showed the contrary to be true: the image of the moon at the horizon is in fact slightly smaller than the moon high up in the sky because the moon is closest to the observer at its zenith, illustrated in fig. 1. Others located the source of the phenomenon on some process of magnification based on refraction because, when the moon is at the horizon, the light rays pass through more of the earth’s atmosphere. It is important to note that according to these explanations the image of the moon would truly be larger in the case of a just risen, or setting moon compared with the image of the moon viewed at its zenith. This is not the case, which can be illustrated in a number of ways.
Early observers found that the image of the moon formed on the screen in a camera obscura has the same diameter, irrespective of the elevation of the moon above the horizon. Similarly, measurements of projections using a lens with a long focal length or photographs of the moon at different locations in the sky reveal no illusion. The fact that there really is no increase in the size of the moon’s retinal image, has been demonstrated by showing that the full moon on the horizon and the moon at its zenith can be equally well covered by a pencil-eraser held at one arm’s length. On the physiological side however, one account claims that owing to accomodative differences in the eyes’ lenses, the retinal image of the moon is actually larger when viewed at the horizon (Roscoe). Another account (Enright) attributes the moon illusion to oculomotor adjustments that induce a phenomenon called micropsia. A sense of how this works can be obtained by doing the following demonstration, called Hering’s maneuver: Hold your thumb out at arm’s length directly below some far object, such as a picture on a wall. Maintain fixation and focus on your thumbnail while moving your thumb closer to you. Notice how the far object appears to shrink in size so long as focus is maintained on the near thumbnail. Enright (1975) confirmed that, even with accomodation errors and changes in the eye’s imaging properties, the size of the retinal image, approximately 0.52°, does not differ enough to account for the moon illusion. Therefore, it has to be concluded that the visual angle that the moon forms at the eye remains essentially the same, regardless of its location, but our perception of its size varies.
Several attempts have been made to quantify the percieved size increase. Minnaert (1940) asked observers to match the percieved size of the moon to one of a series of white discs varying in size on a black background, located at a fixed distance. Of course this can not be done by direct comparison or one would find, just as in the case of an actual measurement, that the size is invariably the same. Minnaert wrote that ‘You must therefore, first look at the moon and impress strongly on your brain how large it looks, then turn round and match that impression with the size of one of the discs’. The numbers obtained this way showed that the moon looks as much as 2.5 to 3.5 times as large near the horizon. Using a similar method Wolfgang Metzger (1953) reported an average increase of factor 2.5. Holway and Boring (1940) estimated that the horizon moon is percieved as about 1.5 times larger than the zenith moon, matching the size of the real moon to that of an adjustable nearby disc. It is obvious that the results obtained by these methods are subject to a fair amount of variability and it was not until the experiments carried out by Rock and Kaufman (1962) that the effect was quantified through direct observation.
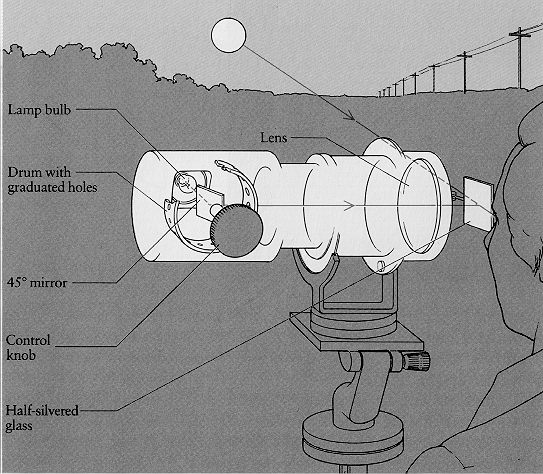
Fig. 2. Apparatus used to similate a moon in the sky. The observer looks through the half silvered glass and sees a reflected disk of light against the sky. Taken from Rock (1984).
Kaufman and Rock constructed a piece of apparatus (fig. 2) that simulated a moon in the sky, producing an image of a disc observed through a colliminating lens, which made the rays of light parallel, so that the eye reacts to them as it does to rays from an infinitely distant object. A rotating drum with graduated holes allowed the observer to change the diameter of the artificial moon while viewing the real horizon or zenith moon. The magnitude of the effect, expressed as the ratio of the percieved size of the horizon moon to the elevated moon, was approximately 1.5 to 1. This ratio appeared to be influenced strongly by the circumstances, e.g. the appearance of the terrain and sky, under which the observations were made. Enright (1975), using the same method, found the ratios varying from 1.5 to 2.
Having established that the moon illusion is a quantifiable perceptual illusion, two important questions arise. Firstly, what mechanism in the visual system gives rise to the Moon Illusion and secondly, under which circumstances can the strongest effect be obtained.
Chapter 1
Possible mechanisms
One recurrent hypothesis is that the illusion is due to tilting of the head back and the eyes upward while viewing the zenith moon. In the nineteenth century the German scientist O. Zoth (1899) tested this idea by hanging milk-glass globes containing lit candles from strings and viewing them from distances as great as 16 meters. At this distance, the cues of convergence and accomodation are no longer effective since the eye will image an object as sharply when it is beyond 6 meters as it does when the object is hundreds of meters away. Zoth estimated that an elevated globe was about 4 percent smaller in size than a globe viewed with head and eyes level. A similar difference in size was found when subjects were asked to match the size of a zenith moon presented on the dome of the Hayden Planetarium in New York to the size of a horizon moon simultaneously presented on the same dome (Kaufman and Rock, 1962). This small magnitude of effect cannot account for the magnitude of the moon illusion which is much greater. An exception to the finding that head and eye elevation produces only a small effect on percieved size is the data obtained in the experiments by Holway and Boring (1940, 1941), mentioned earlier. They showed that when the moon is viewed with eyes elevated, subjects give smaller size matches than they do when the moon is viewed with the eyes level. According to Holway and Boring, head elevation has nothing to do with the the moon illusion, elevation of the eyes, however, does. This would suggest that the percieved size of the horizon moon would decrease if it is observed with elevated eyes.
Rock and Kaufman tried viewing the moon with both levelled and elevated eyes. They saw no change in percieved size. This was consistent with a remark in the papers of Holway and Boring, who reported that they too experienced no change in the size of the moon when they changed the elevation of their eyes. Nevertheless, eye elevation was consistently related to a change in the size of a nearby matched disc. Nevertheless, since the eye elevation effect adds little if anything to the full magnitude of the moon illusion, an alternative theory must be considered.
This theory has an ancient origin and concerns the visual perception of space. In approximately 150 AD Ptolemy theorized that a filled space is percieved as having a greater extent than an equally long but unfilled space. In the eighteenth century, Robert Smith employed Ptolemy’s idea in explaining the moon illusion.
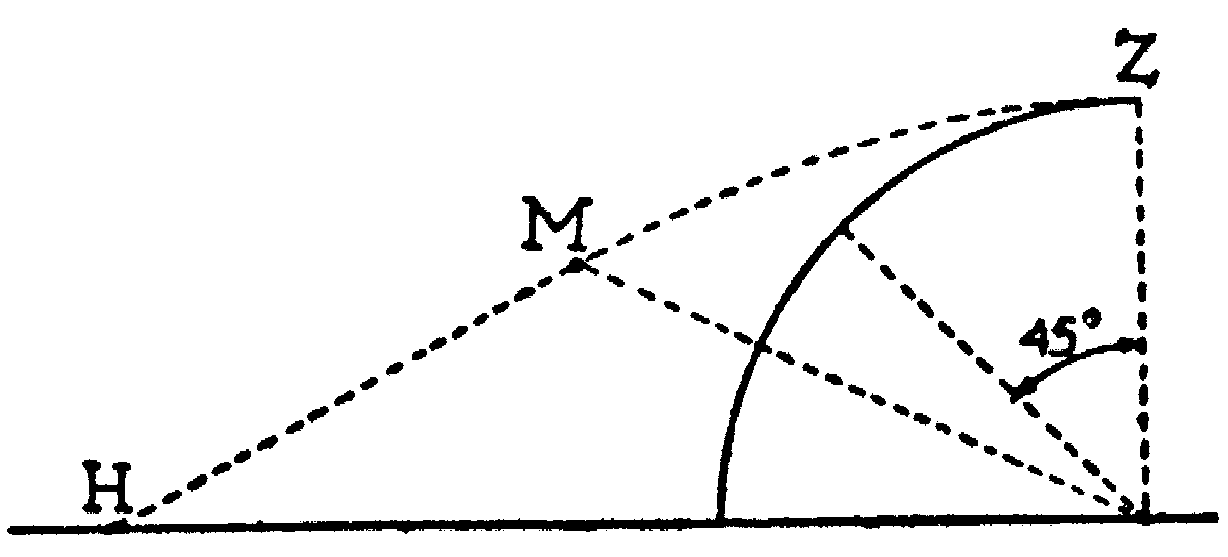
Fig. 3. The division of the apparent arc from zenith to horizon into two parts. Taken from Minnaert (1940).
Although the zenith sky is optically as far away as the horizon sky it is percieved as nearer because it is seen through an unfilled space, which leads to flattening of the dome of the sky (Smith, 1767). Minneart (1940), who referred to the effect as "the Appearent Flattening of the Vault of Heaven" and studied it extensively, formed estimates of the percieved shape of the sky by asking unprejudiced observers to divide the apparent arc from zenith to horizon into two equal parts, illustrated in fig. 3.
The estimated centre of the arc turned out not to lie at an elevation of 45°, but much lower, mostly at elevations from 20° to 30°, which shows that the sky is percieved to be substantially flattened, shown in fig. 4. Minnaert found the apparent flattening to depend on a variety of circumstances. "It increases greatly when the sky is clouded and in the twilight and decreases when the stars shine brightly on dark nights" (c.f. Minnaert, 1940). Also, seen through a piece of red glass, the sky seems flatter; whereas if it is seen through blue glass, the sky seems higher and more spherical. There is no conclusive explanation for this appearent flattening. Fact is that when the sky is covered with clouds, the clouds directly overhead fill more of the visual field than do clouds of similar size but at a greater distance, which is somewhat like looking at a textured terrain while standing on one’s head. It can be argued that this type of experience causes one to ascribe a surfacelike character to the sky whether it has clouds or not (Kaufman, 1979).
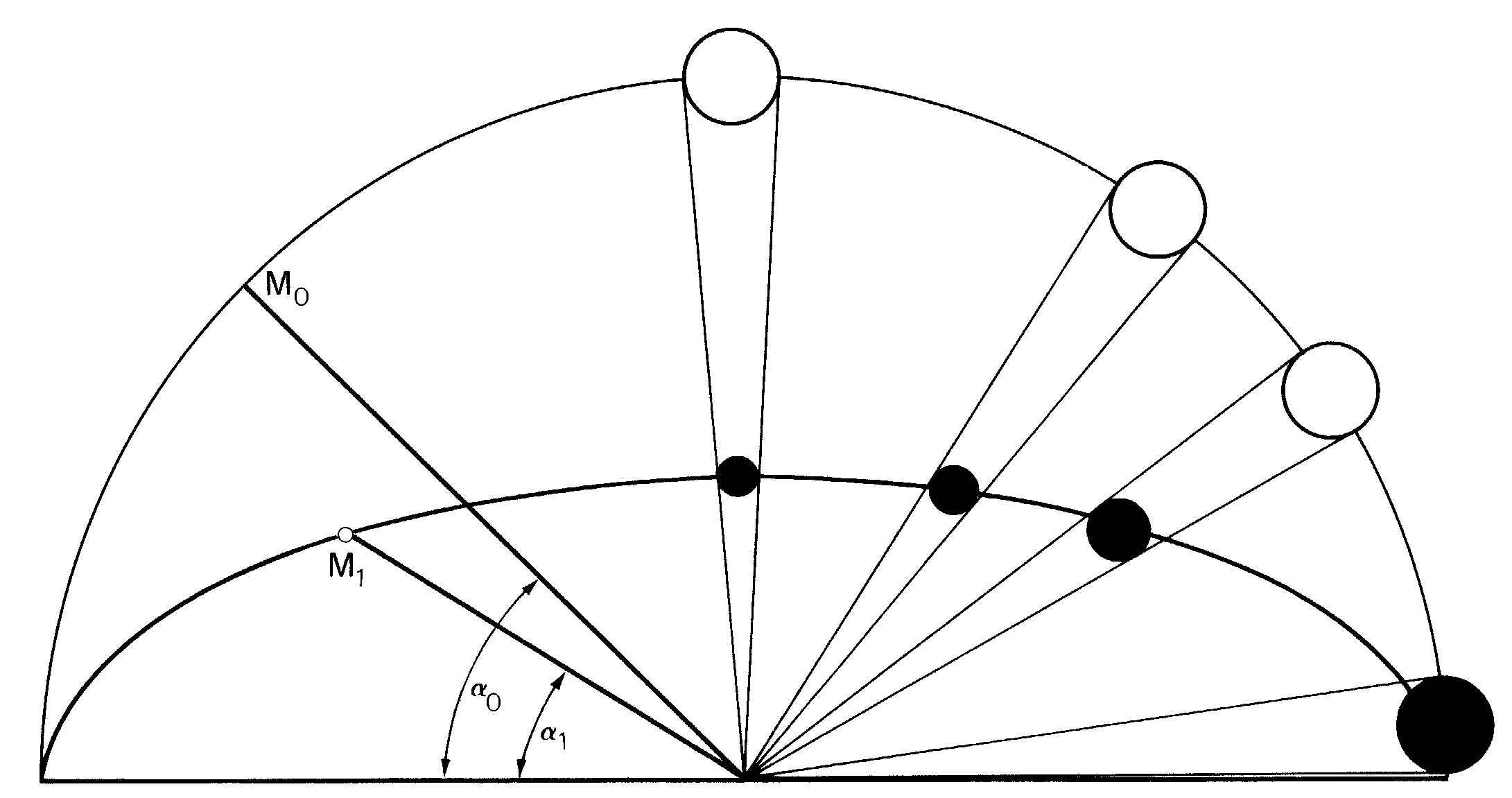
Fig. 4. Proving that the sky appears flattened. The half-arc angle (a 0) would be 45 degrees if the dome of the sky is percieved as spherical. However, if the dome is percieved as flattened, the half-arc angle would be less than 45 degrees, as indicated by a 1. Moreover, if the moon is localised on the flattened sky, it will appear smaller in the zenith than at the horizon. Taken from Kaufman (1979).
A similar theory was developed centuries earlier by the Arab scientist Alhazen, who presented a theory of the moon illusion in the eleventh century. According to Alhazen, our experience with a flat terrain causes us to ascribe a flat characteristic to the blue expanse of the sky. The heavenly bodies are percieved as lying on this flat sky. Nearby objects on the terrain are at our feet, nearby objects in the sky are above our heads and therefore heavenly bodies that lie at lower elevations, are percieved as more distant. In this theory, the moon on the horizon must be the most distant of all heavenly bodies. Objects directly overhead would have to be the closest. Thus, Alhazen independently developed the apparent distance theory associated with Ptolemy and Robert Smith. In addition he presented a conjecture as to why the sky has a flattened shape.
Regardless of whether the explanation given for the effect is correct, there can be little doubt that the sky appears to be relatively flattened and that the apparent flattening is influenced by a number of factors, for example the presence of clouds, stucture of the terrain and the distance to the visible horizon (Minnaert, 1940).
Chapter 2
The perception of distance and size
Despite the increasing or decreasing size of the retinal image (or visual angle) of an object as a function of distance, its apparent size remains more or less the same. Even though a distant man has a small angular size and a nearby man a large angular size, we can usually tell if they have the same or different physical sizes. To percieve size as constant when the object is viewed from various distances, as when a man walks away from you, the visual system needs more than just the visual angle of an object in order to determine its size or this constancy would never be achieved.
According to the stimulus-relation theory, size perception and size constancy can be explained by the ratio of the visual angle of one object to that of other objects, for example, if we see a man standing next to a house, his height bears a definite size relation to the height of the house. That relation will not change, no matter from how far away we view the man. Similarly, an object on a lawn will cover a given number of units of the grass texture. Viewed from a different distance, the object will cover, or occlude, the same number of units. It was suggested by James Gibson (1950) that in these cases percieved-size constancy can be explained by the unvarying size ratio of objects in a scene, without having to refer to distance at all.
Gibson’s theory maintains that constancy does not simply depend upon the occlusion by objects of an equal number of units in the texture of the plane. It also requires that the plane is percieved to be receding in depth with textured units that are percieved as equal and everywhere equidistant from one another. Naturally, if that is true, objects at different distances that cover an equal number of textured units are, almost by definition equal in size. If however, the textured surface does not look like a receding plane, the effect does not occur.
The major reason for rejecting the stimulus-relation explanation is that constancy can be achieved in instances where stimulus relations are not applicable. For example in a dark room with only a single luminous object visible, constancy will hold as long as distance information is available, such as is provided at near distances by, for instance accomodation, convergence of the two eyes and binocular disparity. Yet if the subject is required to view the object with one eye through a small apperture, thus eliminating such cues to distance, constancy fails. Under these conditions, the object’s size appears to be indeterminate - that is, to have no definite objective size at all - and two such subjects will be matched on the basis of visual angle alone (c.f. Rock, 1984).
Rock and Ebenholtz (1959) carried out experiments in which observers had to compare two luminous line segments contained in two rectangles of different sizes, shown in fig. 5. The length of one segment was kept constant at about one third the height of its rectangle. The observers were asked to match the length of this fixed segment by adjusting the line segment in the other rectangle. The result was a tendency to judge the segments as equal when they differed in physical length but filled nearly proportionate amounts of the rectangle, which suggests that at large distances - where there are no discriminating cues to distance from convergence or disparity - the mechanism described in the stimulus relation theory may contribute to the phenomenon of size constancy.
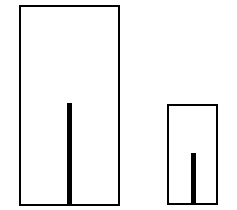 Fig. 5. In circumstances where
there are no direct cues to depth in the visual scene, observers tend
to judge the central lines in the two rectangles as equal in length
when they fill equal proportions of their frames. Taken from Rock and Ebenholz (1959).
Fig. 5. In circumstances where
there are no direct cues to depth in the visual scene, observers tend
to judge the central lines in the two rectangles as equal in length
when they fill equal proportions of their frames. Taken from Rock and Ebenholz (1959).
Later theories of perception yield the well-known size-distance-invariance hypothesis (SDIH) (Gilinsky, 1951; Schlosberg, 1950). The relation between angular size a of an object of a particular height h is inversely proportional to its distance D, which can be expressed as: tan a = h D-1 , from which it follows that: h = D tan a . Therefore, by multiplying some function of the angular size of an object by its distance, its height can be easily computed. For small angles - i.e. smaller than about 7 degrees - the tangents are nearly the same as the angles themselves when the angles are expressed in terms of radians. Consequently, for small angles: a (radians) = h D-1. Thus the height of an object can be computed by multiplying its angular size (in radians) by its distance. Thus, h = D a (radians).
Helmholz (1925), unable to identify the physiological process responsible, invented the concept of unconscious inference. This concept refers to mental processes that depend on sensory information about distance, to which the observer has no conscious access. Richards (1968) suggested that when cues indicate that the distance to an object is increased, the receptive fields of brain cells change in size to compensate for the reduced of the image. Both this and Helmholz’s hypothesis are contradicted by the findings of Gilinsky (1955) which demonstrate that observers may respond either to the true size of the object at a distance, or to its retinal image size, depending on the tasks they must perform.
Alberta Gilinsky placed triangles of the same physical size at several different distances ranging from 30 to 1500 meters from an observer. The observer’s task was to adjust the the size of a nearby triangle until it matched the size of each of the distant triangles. Different observers were given different sets of instructions to do this. Some observers had to match the physical height of the nearby triangle with each of the triangles at different distances. The observers were told to imagine that the adjustable triangle was at the same distance as the triangle being matched and try to equate their sizes. Since all the distant triangles were of the same height, it is to be expected, given size constancy, that the adjustable triangle would always be made to have the same height too, regardless of the distance to the triangle being matched. Observers were able to perform their task very well. This was possible only if the observers could determine that a triangle that subtends a very small angle at the eye is actually equal in physical size to a triangle that subtends a much larger angle - i.e., if they responded in terms of what is called the law of size constancy.
Other observers in this experiment were given different instructions. They were asked to imagine that photographs were taken of both the distant triangle and the nearby adjustable triangle. The distant triangle’s picture would be smaller than the picture of the adjustable triangle, consistent with the law of visual angle. Successful achievement of this task would indicate that observers were also able to respond to differences in relative size of the retinal images even though good cues to distance were available. The observers were reasonably good at this task too: their matches were in much closer agreement with the law of visual angle than they were with the predictions based on the law of size constancy. In other words, this data shows that the observer can be fairly accurately report both linear size, as predicted from the SDIH, and visual angle values of an object, depending on the given instructions. Two decades later, similar findings were reported by Leibowitz and Harvey (1969).
Size constancy is achieved under diverse circumstances, however, it seems clear that information about distance to objects is a major determinant, particularly when objects are relatively nearby. The effect of information about distance on apparent size is perfectly illustrated by the viewing of after-images, for example of a black or illuminated disc against a contrasting background. Through a process called adaptation the relative sensitivities of those cells with receptive fields stimulated by the disc change from those stimulated by the background. When subsequently a homogenously illuminated surface is viewed, a ‘negative image’ of the disc will be seen against its contrasting background.
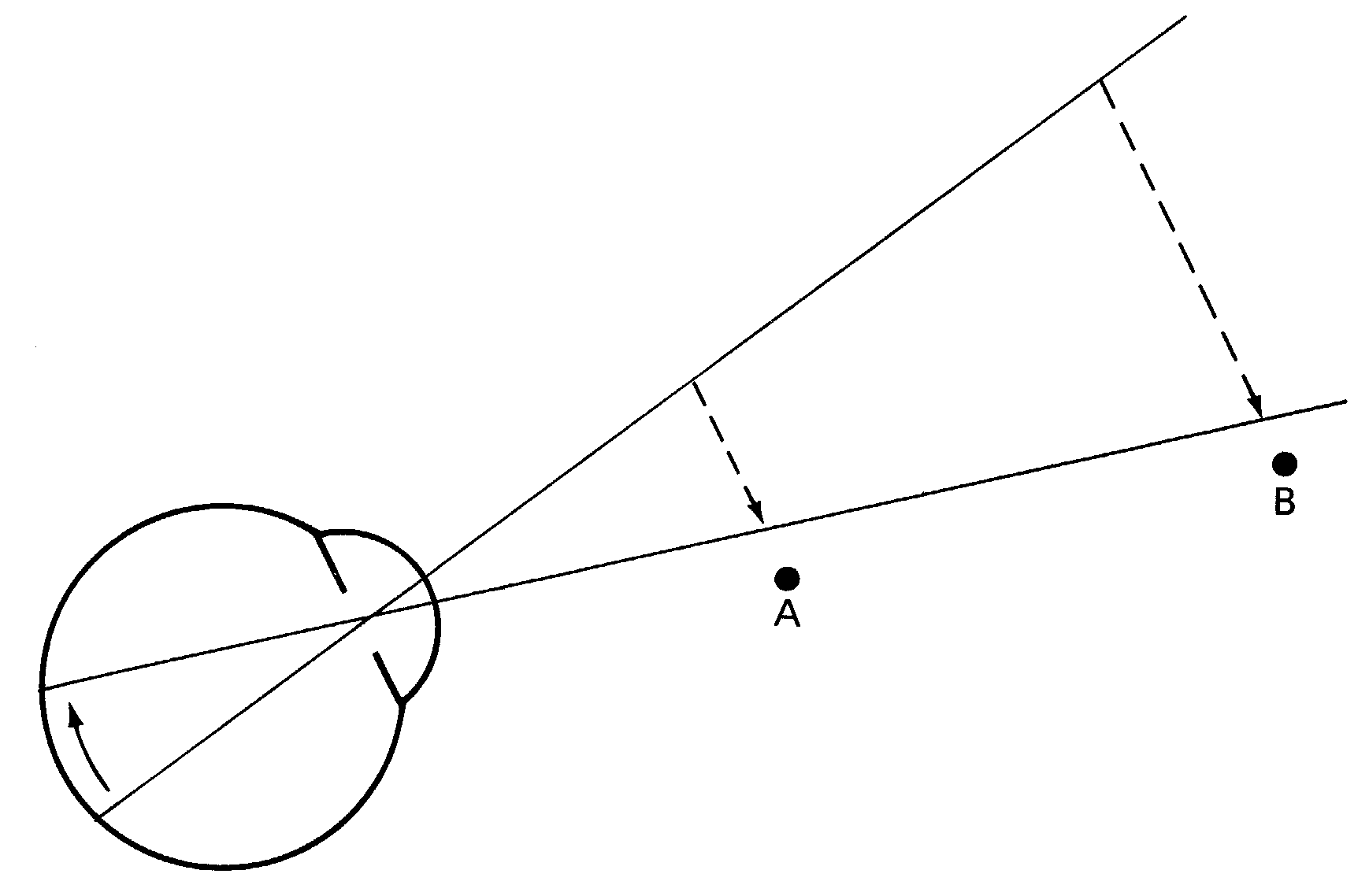
Fig. 6. An after-image, represented by the solid arrow on the retina, is percieved as being twice as large when percieved at B than it is when percieved at A. This examplifies Emmert's law. Taken from Kaufman (1979).
To the visual system, an after-image is located in space and its percieved size is determined by the distance at which it is viewed: when looking at a nearby wall the disc will be seen as smaller than when it is superimposed on a distant wall, illustrated by fig. 6. This is an example of a general rule commonly referred to as Emmert’s law. According to this law, the percieved size of an object of constant angular size is directly proportional to its apparent distance, which is similar to the SDIH. An after-image has a constant angular size. If you percieve it to be at a great distance it will consequently seem larger than it would be if it were percieved as being nearby. Note that in the definition of Emmert’s law, the term apparent distance is used. This is required because the distance at which something is percieved is not necessarily the same as its actual physical distance. A famous example of the influence of apparent distance on percieved size is the Ponzo i
llusion shown in fig. 7. Because of the perspective created by the triangle, the upper cillinder appears to be more distant than the lower one, even though the size of their retinal images is equal. Compliant with Emmerts law, the upper cillinder appears to be larger.
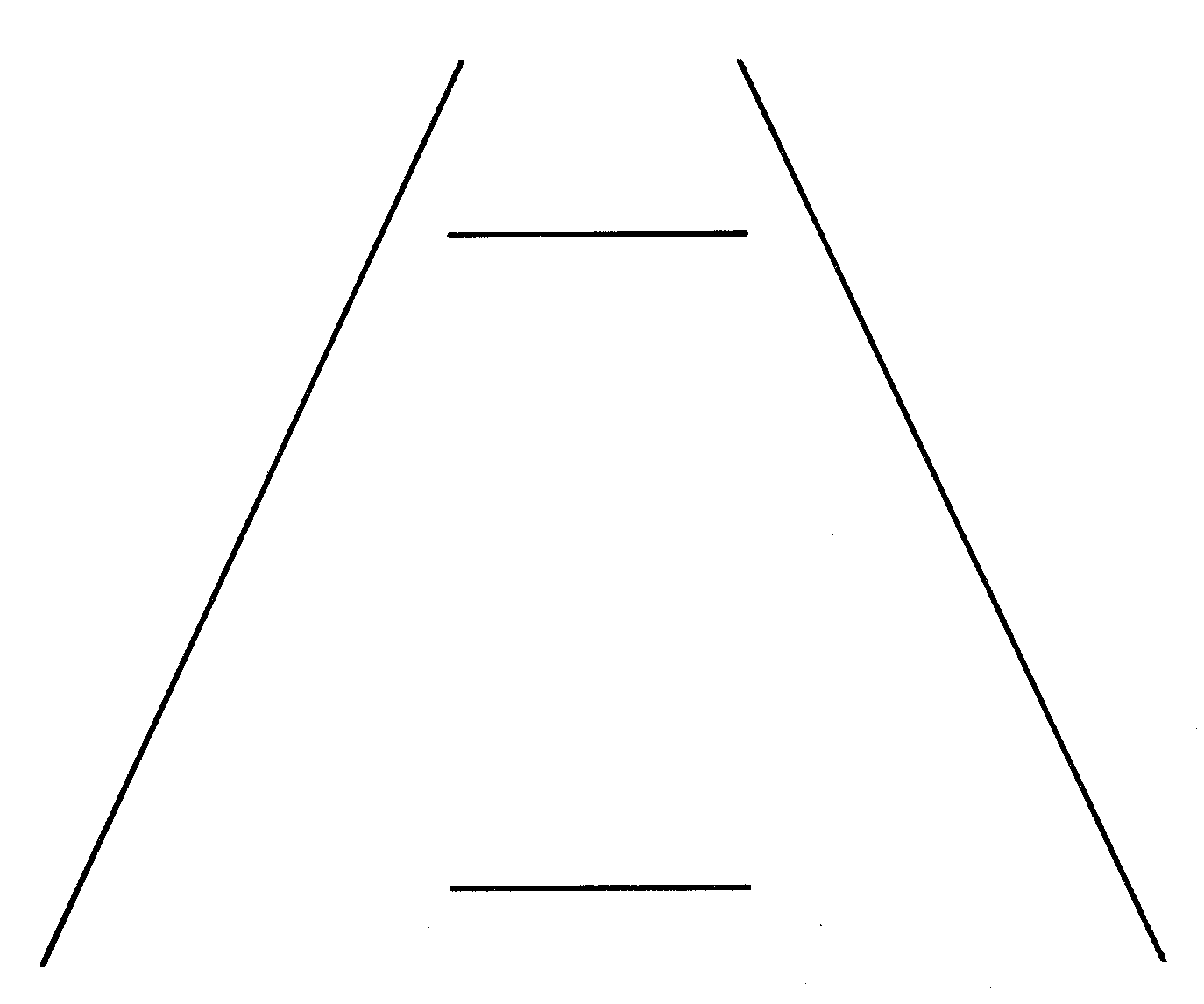
Fig. 7. The Ponzo illusion. Taken from Kaufman (1979).
Considering the retinal angular size of the horizon moon and that of the moon at its zenith to be equal, in a way similar to the adapted retinal area in the case of an after-image, and given the apparent flattening of the sky, as described in the previous chapter, it is not surprising to find that the percieved size of the moon just above the horizon is larger than that of the moon at higher elevations. This was considered to be a conclusive explanation for the moon illusion (Kaufman, 1979; Hershenson, 1984).
Chapter 3
The paradox
Edward Boring, the first psychologist to do formal experiments on the moon illusion, rejected this theory, arguing that when people look at the horizon moon, it appears to be closer, which cannot be more clearly illustrated than by the observation that little children sometimes try to grasp the enormous moon just above the horizon (Metzger, 1953). Other formal and informal tests yield the same reply, the horizon moon usually appears both larger, and closer (McCready, 1984; Loftus, 1985).
According to Rock (1984), this ‘size-distance paradox’ (Epstein et al., 1961) can be explained by assuming that when asked in which position the moon appears to be closer, the observer is comparing moons that already appear to be different in size. Because relative size is a cue to distance and because distant objects are percieved to be smaller, the observer may conclude from the fact that the moon appears larger on the horizon that it also appears closer. This suggests that there are two separate mechanisms at work in the perception of size and distance. The first employs the percieved distance to an object to generate a size percept of the viewed object, whereas the second mechanism generates the apparent distance from the various cues to distance available in the visual scene, including relative size, perspective and image overlap.
This hypothesis is supported by experiments in which observers were asked to judge whether the distance to the empty horizon sky was nearer, or further than the distance to the empty zenith sky. All observers asserted that the horizon sky was further away. In addition, a very large artificial moon was projected onto the zenith sky and a perceptibly much smaller moon was projected onto the horizon sky. In this case, all observers said that the zenith moon was nearer, thus proving that percieved size is the criterion employed when making distance judgements in such circumstances. This leads to a somewhat revised form of the apparent distance theory, stating that the apparent size of an object of constant retinal size is proportional to its percieved, or registred, distance (Kaufman and Rock,1962).
Chapter 4
An alternative view
McCready argued that the ‘taking-into account’ model, which postulates that retinal image size is transformed into apparent size after taking the percieved distance into account, inadvertently leads to a paradox because it omits V’, the apparent visual angle value. For a target subtending a constant visual angle (V rad), the size-distance-invariance hypothesis (SDIH) predicts that the percieved linear size (S’) will be a direct function of the percieved distance (D’) (Emmert’s law, discussed in chapter 2). From the SDIH, positive partial correlations should be obtained between apparent size and visual angle. Several optical illusions, however, like the Ebbinghaus illusion, shown in fig. 8, clearly unbalance the SDIH. The observed size increase of approximatly 20% of the circle that is surrounded by small circles can, according to The SDIH and Emmert’s law, be recorded only if this circle is percieved to be 20% farther away than the circle surrounded by large circles. The common report is that circle 2 looks larger and on the same page as circle 1, this size distance paradox is shown to occur for many other illusions.
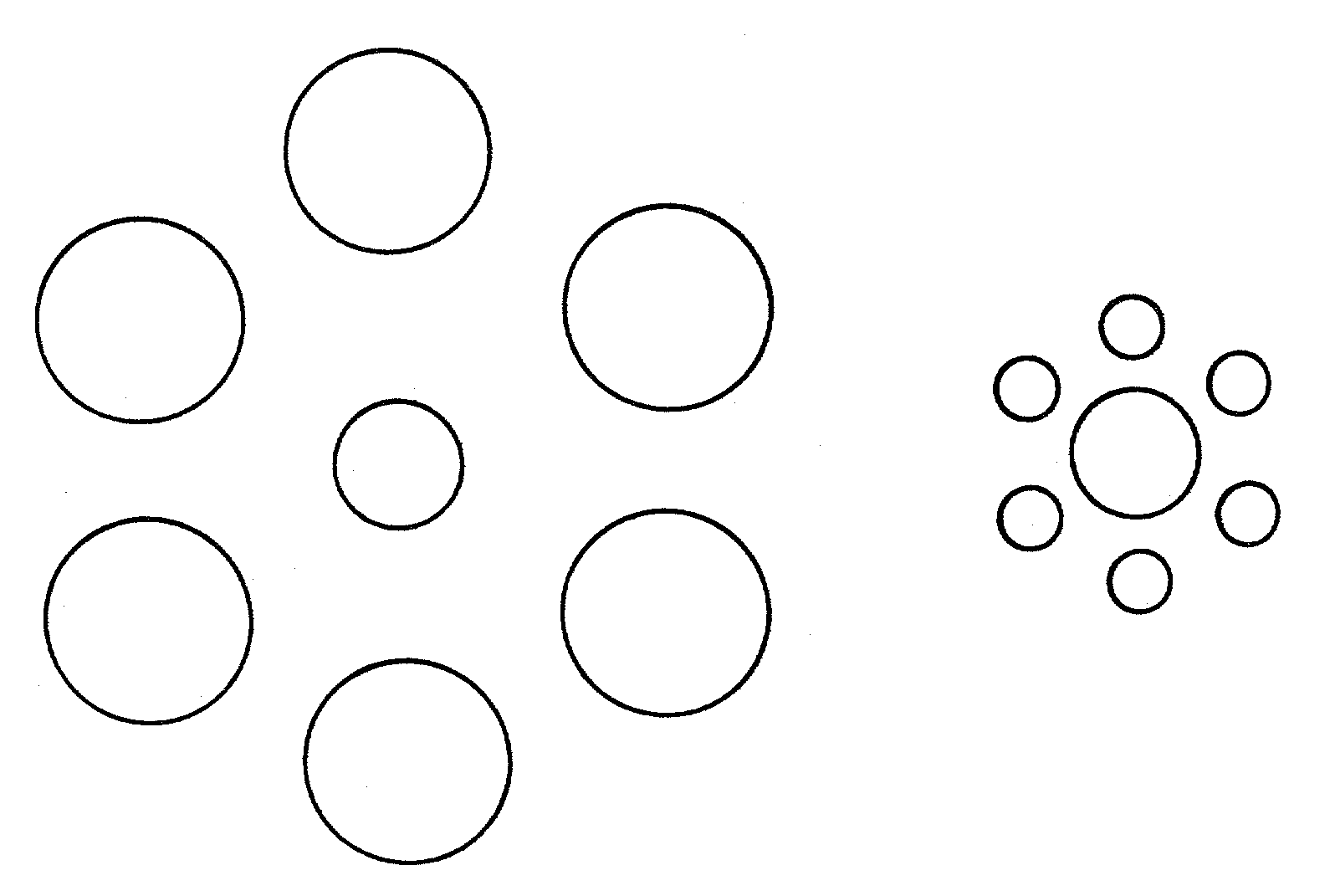
Fig. 8. The Ebbinghaus illusion is that the diameter of the second circle, surrounded by smaller circles, appears to subtend a greater visual angle than the diameter of the first circle, surrounded by larger circles. Taken from McCready (1985).
The paradoxes vanish, however, when these optical illusions, including the Ebbinghaus and the moon perception, are redefined as examples of misperceptions of visual angle (V) values (McCready, 1965, 1985, 1986). That is, the equivocal report "looks 20% wider" is properly recorded first as V2’ = 1.2 V1’. The illusion thus mimics a veridical perception for a visual angle ratio of V2/V1 = 1.2, obtained with either a pair of equidistant circles, with S2 = 1.2 S1, or a pair of equal linear sizes (S2 = S1), with D2 = 0.83 D1.
In the case of the the moon illusion V’ does not equal V, so the ratio value S’/D’ does not equal S/D. McCready contended that the moon illusion could be accounted for if the apparent visual angle of the moon decreased as the moon ascended. Nevertheless, he did not attempt to measure this apparent visual angle because its apparent extent is so small (0.52°) that it is very difficult to measure.
Higashiyama (1992, 1994) undertook a series of experiments in which observers were asked to give a verbal estimate of size and distance of a number of islands, 1.1 to 10.4 km from a sightseeing platform, and in a second series, from a boat. The results showed that size and distance estimates vary in proportion to objective size and distance, respectively. The size estimates for the long-distance targets are easily explained if apparent distance is taken into account in estimating apparent size. However, other aspects of the partial correlation analysis, (i.e., a high positive correlation between visual angle (V) and apparent distance (D’) and a high negative correlation between V and apparent size (S’)) do not support the taking-into-account model.
It may also be difficult to explain the size estimates by texture gradient given on the retina, because there was no or little texture gradient behind the very far stimulus targets. The targets were seen on the background of the sky and the sea. The sky does not provied texture gradient at all, and the waves on the sea may provide texture gradient at short distances, but not at long distances. A prominent feature of the partial correlations obtained for the data of the experiments is that size and distance estimates were contaminated by a cognitive bias. The negative correlation between objective distance (D) and S’ indicates that a farther objects appears smaller, and the negative correlation between S and D’ indicates that a smaller object appears more distant. These tendencies may resemble the perspective attitude- a belief that an object appears small at a great distance, even when size constancy actually prevails over long distance (Carlson, 1977). Higashiyama postulated that it is likely that when there is not much reliable external information for size estimation, the estimation is determined not only by the external information, but also by cognitive strategies, such as the perspective attitude, which has been considered to distort size-constancy judgments. Summarizing, the obtained values of S’ / D’ did not conform to the equation derived from the SDIH. Instead the values were reasonably represented be an equation which assumes S’ / D’ to be a function of apparent visual angle. The data showed that the mean visual angle of stimulus targets (13.5°) was percieved as 18.5° on the average. From this it was concluded that although the importance of apparent distance should not be disregarded when we consider the perception of size, for extremely distant objects such as the moon, apparent distance is not as critical as apparent visual angle.
Higashiyama came to a conclusion similar to that of McCready, stating that the moon illusion may be difficult to explain as long as it is assumed that apparent visual angle is processed in proporion to actual visual angle. Where McCready was not able to measure the apparent visual angle, Higashiyama shows that the ratio between the visual angle of the horizon moon and the moon at its zenith can be derived from the equations that he formulated for describing the relation between objective and apparent visual angle of very far objects, fig. 9. The degree of fit may not be perfect, but the trend that the moon appears smaller as it ascends is largely explainable in terms of the moon’s apparent visual angle.

Fig. 9. The ratio of apparent size of the moon at different elevations (in degrees) to the apparent size of the horizon moon. The parameter is the data from three subjects in Holway and Boring (1940). The three smooth lines are predicted from equations desrcibing the relation between retinal visual angle (V) and apparent visual angle (V'), postulated by Higashiyama (1992). Figure taken from Higashiyama (1992).
From this it is concluded that although the importance of apparent distance should not be disregarded when we consider the perception of size, for extremely distant objects such as the moon, apparent distance is not as critical as apparent visual angle.
Now the major problem has become why Vh’ exceeds Vz’. The answer to this may be found by asuming a more direct role for cognitive cues to distance. As Rock, Shallo, and Schwartz (1978) showed, the more an observer recognizes, interprets and accepts that a viewed pattern indicates large depth values (large distance differences), the more V’ increases for a target of constant V located at a nominally "far" place in the visual world. The question thus is why distance-cue variables control the ratio V’/V. One option given by Higashiyama are cognitive strategies such as perspective attitudes. Furthermore, McCready presents an oculomotor explanation as the major source of the V illusions that initiate the moon illusion, involving accomodation-convergence micropsia (AC-minification). This was suggested earlier by Enright (1975), but realising that this is not conclusive, McCready expresses the hope to elaborate on this inconclusive hypothesis sometime in the future.
Chapter 5
The moon illusion optimized
Even though there is no conclusive description of the details of the mechanism underlying the moon illusion, the various hypotheses do provide clues as to the circumstances that provide the strongest illusionary effect.
Both the classic explanation, in essence given by Alhazen, and in a modified form proposed by Kaufman, Rock and Hershenson, as well as the current descriptions by McCready and Higashiyama, suggest that visual cues to distance play an important role.
This may explain the legendary sunsets in Africa and the enormous moon rising from the horizon at sea. Under these circumstances the visible horizon is percieved to be so far away, due to terrain texture and the flatness of the prairy, desert or the ocean surface, that the difference in size between the horizon and zenith moon will be relatively large compared with the apparent sizes in a mountain landscape with a relatively near visible horizon. This was illustrated by Minnaert, who showed that the apparent size increase of the moon over a distant horizon (> 10 km) at an airport was reported to be larger than the increase observed over a nearby forest, creating a visible horizon at approximately 2 km from the observers.
Also, cloud conditions and illumination or luminance contrast seem to play an important role. The illusion is stronger when there are clouds in the sky compared with a cloudless sky and the apparent size increase is strongest at twighlight. Another factor influencing the effect is structure in the terrain over which the moon is viewed. A row of houses or a railway track provide perspective cues to distance which, in some way result in an increased apparent visual angle. Even though this sort of structure is absent at open sea the moon illusion is also reported by sailors and airline pilots. Rock (1975) stressed that "contrary to widespread belief, the moon illusion does not require comparisson of the moon with familiar objects on the ground, such as houses or trees". Presumably, clouds play an even more important role under these circumstances.
A complementary illusion is that inverted (up side down) viewing of the landscape typically makes all horizon objects, including the moon look smaller and farther away (Washburn, 1894): the inversion minifies all apparent size values, including those for buildings, trees, hills, clouds and the moon. Restoring the upright scene, with its familiar arrangements of contextual cues to great depths, then magnifies apparent size values back to their former values.
Another situation in which the illusion does not occur is when the moon is viewed through an aperture or cillinder, occluding the environment. When the moon is viewed this way monocularly, the moon will appear small as when it is high up in the sky. When the horizon moon is simultaneously viewed through a cillinder with one eye and viewed normally with the other eye, remarkably enough, the apparent size of the moon seen by each eye will be different.
Kaufman and Rock (1962) occluded sight of the terrain with cardboards or when observers were asked to view the moon in the dark in the Hayden Planetarium. In a further experiment, mirrors were used to create the impression of a terrain for the elevated ‘moon’, so that, in looking upward, the observer saw the ground rising in a vertical direction. Similarly, mirrors were used to eliminate the sight of the terrain ordinarily visible below the horizon moon, so that in looking straight ahead, the observer saw only sky. According to Minnaert this kind of experiment is very difficult to perform: ‘Now, do not try to check this further by judging the apparent size of sun and moon in a mirror so that in this way you see, for instance, the moon high up while your gaze is directed horizontally. If the observer is conscious of the presence of a mirror in any way, the illusion is partly lost.’ However, under the conditions set by Kaufman and Rock the illusion was truly reversed: the elevated moon appeared larger.
Conclusion
The ‘taking-into-account’ model of size perception, where retinal image size is transformed into apparent size is after taking apparent distance into account, is not longer a valid explanation of the moon illusion. First proposed in the eleventh century by Alhazen and later postulated in a more refined form, the size distance invariance hypothesis (SDIH) by Kaufman (1979), this explanation inadvertantly leads to a paradox when experimental finding are considered. The paradox can only be avoided by assuming that size is determined from percieved distance, from which subsequently the apparent distane is determined.
McCready (1985, 1986) postulated that the shortcomming of the size distance invariance hypothesis (SDIH) lie in the fact that it omits the apparent visual angle. Tests by Higashiyama (1992, 1994) support the importance of the apparent visual angle in the perception of size and distance of very far objects, and experimental data is indeed in accordance with this theory, central to which is the difference between the visual angle (V) and the apparent visual angle (V’) and also the difference between V’ of the horizon moon and V’ of the moon at its zenith.
The question now has become: why is the ratio V’h / V different from V’z / V. Possible answers may include the classic cues to depth, including perspective, image overlap, parallax or novel concepts including contour (neural) interactions, oculomotor effects and accomodation-convergence micropsia (AC minification).
The moon illusion will undoubtedly contribute to the theory of normal size-distance perception, as "the study of the illusions of the senses is... a very prominent part of the study of the senses; for just those cases which are not in accordance with reality are particularly instructive for discovering the laws of those means and processes by which normal perception originates.", Helmholz (1925).
References
Carlson, V.R., 1977. Instructions and perceptual constancy judgements. In W. Epstein (Ed.), Stability and constances in visual perception: Mechanisms and Processes. New York: Wiley
Enright, J.T., 1975. Moon illusion examined from a new point of view. Proceedings of the American Philosophical society, 119, 87-107
Epstein, W., 1973. The process of ‘taking-into-account’ in visual perception. Perception, 2, 267-285
Epstein, W., Park, J. and Casey, A., 1961. The current status of the size-distance hypothesis. Psycological Bulletin, 58, 491-514
Gibson, J.J., 1950. Perception of the visual world. Houghton Mifflin, Boston
Gibson, J.J., 1979. The ecological approach to visual perception. Houghton Mifflin, Boston
Gilinsky, A.S., 1955. The effect of attitude upon the perception of size. American Journal of Psychology, 68, 173-192
Gogel, W.C., 1990. Peer
Gutzwiller, M.C., 1998. The oldest three-body problem. Reviews of Modern Physics, 70 (2), 589-639
Helmholz, H. von, 1925. Treatise on physiological optics. vol. 3, Trans. from 3rd German ed., J. P. C. Southall, ed. Opt. Soc. Amer., Republished New York: Dover 1962.
Hershenson, M., 1989. The moon illusion. Hillsdale, NJ: Erlbaum
Higashiyama, A., 1992. Anisotropic perception of visual angle: Implications for the horizontal-vertical illusion, overconstancy of size and the moon illusion. Perception & Psychophysics, 51, 218-230
Higashiyama, A. and Shimono, K., 1994. How accurate is size and distance perception for very far terrestrial objects? Function and causality. Perception & Psychophysics, 55, 429-442
Holway, A.F. and Boring, E.G., 1940. The Moon illusion and the angle of regard. American Journal of Psychology, 52, 509-516
Holway, A.H. and Boring, E.G., 1941. Determinants of apparent visual size with distance variant. American Journal of Psychology, 54, 21-37
Landauer, A.A. and Epstein, W., 1969. Does retinal size have a unique correlate in percieved size? Perception and Psychophysics, 6, 273-275
Leibowitz, H.W. and Harvey, L.O., 1969. Effects of instructions, environment, and type of test objects on machted size. Journal of experimental Psychology, 81, 36-43
McCready, D., 1965. Size-distance perception and accomodation-convergence micropsia: A critique. Vision Research, 5, 189-206
McCready, D., 1985. On size, distance and visual angle perception. Perception & Psychophysics, 37, 323-334
McCready, D., 1986.Moon illusions redescribed. Perception & Psychophysics, 39, 64-72
Metzger, W., 1953. Gesetze des Sehens. Verlag von Waldemar Kramer, Frankfurt
Minnaert, M., 1940. Light & Colour in the open air. G. Bell and sons, London.
Kaufman, L., 1979. Perception. Oxford University Press, New York.
Kaufman, L. and Rock, I., 1962. The moon illusion. I. Science, 136, 953-61
Smith, R., 1767. Cours complet d’Optique. a Avignon, Gerard (vf) & F. Sequin, vol. 1, 116-23
Richards, W., 1968. Spatial remapping in the primate visual system. Kybernetic, 68, 173-92
Reimann, E., 1902. Die scheinbare Vergrosserung der sonne und des Monde am Horizont. Z. f. Psychol., 30, 1-38,161-95
Rock, I., 1984. Perception. Scientific American Books, New York.
Rock, I. and Ebenholtz, S., 1959. The relational determination of percieved size. Psychol. Rev., 66, 387-401
Weintraub, D.J. and Gardner, G.T., 1970. Emmert’s laws: Size constancy versus optical geometry. American Journal of Psychology, 83, 40-54
Zoth, O., 1899. Über den Einfluss der Blickrichtung auf die schienbare Grosse der Gestirne und die schienbare Form des Himmelgewolbes. Arch. f. d. ges. Physiol. 78, 363-401